Школа № 179 из 6 в 7 класс 2025 год

Школа №179

2025 год

21.03.2025

1. ($1$ балл) Поликарп очень спешит на вступительные испытания в $179$ школу. Папа везёт его на автомобиле, и за $25\%$ от минуты они проезжают $40\%$ километра. Какова скорость автомобиля в километрах в час?
2. ($1$ балл) Серёже нравятся числа и задачи про них. Он придумал трёхзначное число. Если в нём первую цифру увеличить на $2$, вторую цифру увеличить на $4$, а третью цифру увеличить на $6$, то в результате всё число увеличится в три раза. Какое число придумал Серёжа?
3. ($2$ балла) Решите уравнение. Если решений несколько, то в ответ запишите их сумму. \[ \left|\left|2-|x+5|\right|-3\right|=1. \]
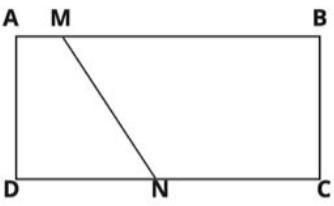
4. ($2$ балла) В прямоугольнике $ABCD$ точка $M$ делит сторону $AB$ в отношении $1:6$, считая от точки $A$, а точка $N$ делит сторону $CD$ в отношении $3:4$, считая от точки $D$. Найдите отношение площади $AMND$ к площади $BCNM$.
   
5. ($3$ балла) Боря на уроках занимается просторонними вещами. Сегодня он на алгебре нашёл себе новое развлечение: взял у сестры детскую пирамидку и сломанную машинку и стал играть. На ось от пирамидки он стал надевать колёса со спицами от сломанной машинки и крутить их. Когда Мария Александровна первый раз взглянула сверху на это, то увидела картинку, изображённую слева, а через минуту — картинку, изображённую справа.
   
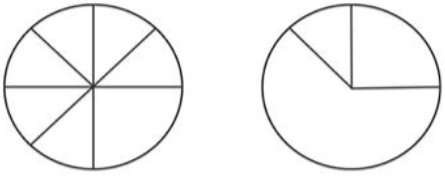
   1. Могло ли у Бори быть три колеса?
   2. Могло ли у Бори быть два колеса?
   Свой ответ обоснуйте.
6. ($3$ балла) Маша и Даня дежурят на вступительных и тихонько играют в среднее арифметическое. Маша написала несколько чисел на листочке, Даня посчитал их среднее арифметическое и запомнил результат. Маша дописала число $15$, Даня посчитал, что среднее арифметическое увеличилось на $2$. Маша дописала число $1$, а Даня посчитал, что среднее арифметическое теперь уменьшилось на $1$ (от последнего результата). Сколько чисел было написано Машей изначально?
7. ($3$ балла) Работница столовой Нина Ивановна моет к завтраку яблоки в огромном чане в тёплой воде. Из горячего крана этот чан заполняется водой за $17$ минут, а из холодного — за $11$ минут. Через сколько минут после начала Нина должна открыть холодный, чтобы к тому моменту, как чан будет полностью заполнен, горячей воды в нём было на треть больше, чем холодной?

Решения задач

1. Поликарп очень спешит на вступительные испытания в $179$ школу. Папа везёт его на автомобиле, и за $25\%$ от минуты они проезжают $40\%$ километра. Какова скорость автомобиля в километрах в час?
   Решение:
   $25\%$ минуты = $\frac{1}{4}$ мин = $\frac{1}{4 \cdot 60}$ ч = $\frac{1}{240}$ ч.
   $40\%$ км = $0,4$ км.
   Скорость $v = \frac{0,4}{\frac{1}{240}} = 0,4 \cdot 240 = 96$ км/ч.
   Ответ: 96.
2. Серёже нравятся числа и задачи про них. Он придумал трёхзначное число. Если в нём первую цифру увеличить на $2$, вторую цифру увеличить на $4$, а третью цифру увеличить на $6$, то в результате всё число увеличится в три раза. Какое число придумал Серёжа?
   Решение. Пусть Серёжа придумал трёхзначное число с цифрами $a$, $b$, $c$: \[ N = 100a + 10b + c. \] По условию, если первую цифру увеличить на $2$, вторую на $4$, а третью на $6$, то всё число увеличится в $3$ раза. Новое число: \[ 100(a+2) + 10(b+4) + (c+6). \] Составим уравнение: \[ 100(a+2) + 10(b+4) + (c+6) = 3(100a + 10b + c). \] Раскроем скобки слева: \[ 100a + 200 + 10b + 40 + c + 6 = 3(100a + 10b + c), \] \[ 100a + 10b + c + 246 = 3(100a + 10b + c). \] Заметим, что $100a + 10b + c = N$, тогда: \[ N + 246 = 3N. \] Перенесём $N$ в правую часть: \[ 246 = 2N \quad\Rightarrow\quad N = 123. \] Проверка: $1+2=3$, $2+4=6$, $3+6=9$, новое число $369$, а \[ 123 \cdot 3 = 369. \] Ответ: $123$.
3. Решите уравнение. Если решений несколько, то в ответ запишите их сумму. \[ \left|\left|2-|x+5|\right|-3\right|=1. \] Решение: \[ \left| \left| 2 - |x+5| \right| - 3 \right| = 1 \] Возможные случаи:
   Случай 1: $\left|2 - |x+5|\right| - 3 = 1$
   $\left|2 - |x+5|\right| = 4$
   Подслучай 1a: $2 - |x+5| = 4$ — Решений нет, так как $|x+5| \geq 0 \Rightarrow 2 - |x+5| \leq 2$.
   Подслучай 1b: $2 - |x+5| = -4 \Rightarrow |x+5| = 6 \Rightarrow x+5 = \pm 6 \Rightarrow x = 1$ или $x = -11$.
   Случай 2: $\left|2 - |x+5|\right| - 3 = -1$
   $\left|2 - |x+5|\right| = 2$
   Подслучай 2a: $2 - |x+5| = 2 \Rightarrow |x+5| = 0 \Rightarrow x = -5$.
   Подслучай 2b: $2 - |x+5| = -2 \Rightarrow |x+5| = 4 \Rightarrow x+5 = \pm 4 \Rightarrow x = -1$ или $x = -9$.
   Все решения: $1$, $-11$, $-5$, $-1$, $-9$. Сумма: $1 + (-11) + (-5) + (-1) + (-9) = -25$.
   Ответ: -25.
4. В прямоугольнике $ABCD$ точка $M$ делит сторону $AB$ в отношении $1:6$, считая от точки $A$, а точка $N$ делит сторону $CD$ в отношении $3:4$, считая от точки $D$. Найдите отношение площади $AMND$ к площади $BCNM$.
   Решение:
   Возьмем сторону AB и CD за 7x.
   Так как ABCD прямоугольник (по улосвию), то сторона AB параллельна стороне DC. Следовательно угол AMN = углу CNM и угол BMN = углу MND как накрест лежащие углы при параллельных прямых следовательно четырехугольники AMDN и BCNM подобные, а значит их площади имеют то же оотношение, что и стороны.$\frac{AM}{NC}=\frac{x}{4x}=\frac{1}{4}$ , следовательно площади относятся $\frac{1}{4}$ Ответ: $\frac{1}{4}$.
5. Ответ.
   1) Три колеса у Бори быть могли.
   2) Два колеса у Бори быть не могли.
   Обоснование.
   На правом рисунке видны только три направления спиц (вертикальное, горизонтальное и одно диагональное). Это значит, что у \emph{каждого} колеса спиц не больше трёх: если бы у какого-то колеса было хотя бы четыре спицы, то как бы ни были повернуты другие колёса, сверху было бы видно не менее четырёх разных направлений спиц, а на рисунке их только три.
   Следовательно, одно колесо даёт не более трёх направлений спиц. Тогда два колеса вместе дают не более \[ 3 + 3 = 6 \] разных направлений, а на левом рисунке видно $8$ направлений спиц. Значит, двумя колёсами получить левый рисунок нельзя, то есть двух колёс быть не могло.
   Покажем, что трёх колёс достаточно. Можно взять три колеса с суммарно восьмью спицами так, чтобы при некотором их взаимном положении сверху были видны спицы во всех восьми направлениях (как на левом рисунке). Затем, повернув колёса относительно друг друга, можно совместить все спицы в трёх направлениях (как на правом рисунке). Таким образом, три колеса устроить можно.
   Итак, трёх колёс быть могло, а двух — нет.
6. Маша написала несколько чисел, их среднее увеличилось на 2 после добавления 15 и уменьшилось на 1 после добавления 1. Сколько чисел было изначально?
   Решение: Пусть изначально было $n$ чисел, сумма $S$. Уравнения: \[ \begin{cases} \frac{S +15}{n + 1} = \frac{S}{n} + 2 \\ \frac{S +16}{n + 2} = \frac{S}{n} + 1 \end{cases} \] Решая систему, получаем $n = 4$.
   Ответ: 4.
7. Чан заполняется горячей водой за $17$ минут и холодной за $11$ минут. Нужно открыть холодный кран через $x$ минут после начала, чтобы горячей воды было на треть больше.
   Решение. Пусть объём чана равен $1$. Тогда скорости заполнения таковы: \[ \text{горячая вода: } \frac{1}{17} \text{ чана в минуту},\qquad \text{холодная вода: } \frac{1}{11} \text{ чана в минуту}. \] Пусть чан полностью заполнится через $T$ минут после открытия горячего крана. Холодный кран Нина откроет через $x$ минут после начала, значит: горячая вода течёт $T$ минут, а холодная — $T - x$ минут. По условию, горячей воды в чане в конце на треть больше, чем холодной, то есть \[ \frac{\text{горячая}}{\text{холодная}} = \frac{4}{3}. \] Тогда доли объёма: \[ \text{горячая вода} = \frac{4}{7},\qquad \text{холодная вода} = \frac{3}{7}. \] Объём горячей воды: \[ \frac{T}{17} = \frac{4}{7} \quad\Rightarrow\quad T = 17 \cdot \frac{4}{7} = \frac{68}{7}. \] Объём холодной воды: \[ \frac{T - x}{11} = \frac{3}{7}. \] Подставим найденное $T$: \[ \frac{\frac{68}{7} - x}{11} = \frac{3}{7}. \] Умножим на $11$: \[ \frac{68}{7} - x = \frac{33}{7}, \] \[ x = \frac{68}{7} - \frac{33}{7} = \frac{35}{7} = 5. \] Значит, холодный кран нужно открыть через $5$ минут после начала. Ответ: через $5$ минут.