Школа № 179 из 6 в 7 класс 2025 год

ГИМНАЗИЯ №1567

2025 год

14.03.2025

1. ($1$ балл) Решите уравнение \[ 0{,}125\left(\dfrac{8}{9}x+8\right)=0{,}2\left(\dfrac{5}{6}x+2\tfrac{1}{3}\right)+2. \]
2. ($2$ балла) По пятницам Ульяна, Аня и Лиза ходят на волейбол. Петя посчитал, сколько каждая из них сделала прыжков за двухчасовую тренировку. Оказалось, что количество прыжков Ульяны относится к количеству прыжков Ани как $7:3$, а количество прыжков Лизы относится к количеству прыжков Ани как $4:5$. Сколько прыжков за тренировку сделала Ульяна, если она сделала на $92$ прыжка больше Лизы?
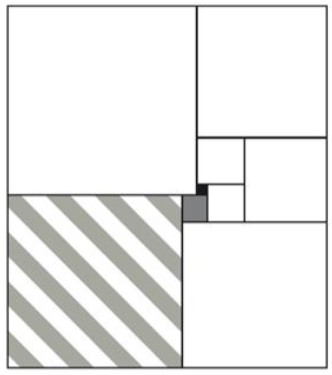
3. ($2$ балла) Егор любит сложные задачи по геометрии. Он сложил из нескольких квадратов вот такой прямоугольник. Сторона самого маленького чёрного квадрата равна $2$ см, а сторона серого квадрата равна $5$ см. Найдите сторону полосатого квадрата.
   
4. ($2$ балла) Решите уравнение. Если решений несколько, то в ответ запишите их сумму. \[ \left|\,|2x+1|-5\,\right|=6. \]
5. ($2$ балла) Найдите наименьшее число $n$ такое, что $n!$ делится на $2025^2$.
   Примечание: по определению $n!=1\cdot 2\cdot 3\cdots n$, например, $3!=1\cdot 2\cdot 3$.
6. ($3$ балла) Некоторые ученики $179$ школы ходят на большой перемене за бургером во «Вкусно и точка». Злата и Аня вышли одновременно из школы, но каждая пошла независимо от другой со своей постоянной скоростью за бургером (и картошечкой!). Когда Аня прошла $120$ метров, Злата прошла всего $100$ метров. А когда Ане оставалось $60$ метров, Злате оставалось целых $140$ метров. Сколько метров составляет длина дороги от школы до «Вкусно и точка»?
7. ($3$ балла) Поступающие в $7$ маткласс разобрались по аудиториям, ждут начала экзамена и болтают. В процессе разговоров выяснилось, что в одной из аудиторий $20\%$ учеников, интересующихся химией и историей, интересуются ещё и физикой, а $25\%$ учеников, интересующихся биологией и историей, интересуются также и информатикой. И только Поликарп и Авдотий любят только математику и ничего кроме неё. Сколько человек в этой аудитории, если известно, что их больше $20$, но меньше $30$?

Решения задач

1. Решите уравнение \[ 0{,}125\left(\dfrac{8}{9}x+8\right)=0{,}2\left(\dfrac{5}{6}x+2\tfrac{1}{3}\right)+2. \] Решение: Переведём десятичные дроби в обычные и смешанные числа в неправильные дроби: \[ \frac{1}{8} \cdot \left( \frac{8x}{9} + 8 \right) = \frac{1}{5} \cdot \left( \frac{5x}{6} + \frac{7}{3} \right) + 2 \] Упростим обе части: \[ \frac{8x}{9 \cdot 8} + \frac{8}{8} = \frac{5x}{6 \cdot 5} + \frac{7}{3 \cdot 5} + 2 \] \[ \frac{x}{9} + 1 = \frac{x}{6} + \frac{7}{15} + 2 \] Найдём общий знаменатель (90) и умножим все члены: \[ 10x + 90 = 15x + 42 + 180 \] \[ 10x + 90 = 15x + 222 \] Перенесём слагаемые: \[ -5x = 132 \quad \Rightarrow \quad x = -26{,}4 \] Ответ: $-26{,}4$.
2. По пятницам Ульяна, Аня и Лиза ходят на волейбол. Петя посчитал, что количество прыжков Ульяны относится к количеству прыжков Ани как $7:3$, а количество прыжков Лизы относится к количеству прыжков Ани как $4:5$. Сколько прыжков за тренировку сделала Ульяна, если она сделала на $92$ прыжка больше Лизы?
   Решение: Пусть прыжки Ани = $15k$ (чтобы привести к общему кратному для отношений $3$ и $5$):
   Ульяна : Аня = 7 : 3 = 35 : 15
   Лиза : Аня = 4 : 5 = 12 : 15
   Тогда Ульяна = $35k$, Аня = $15k$, Лиза = $12k$
   Разница между Ульяной и Лизой: $35k - 12k = 23k = 92 \Rightarrow k = 4$
   Следовательно, Ульяна сделала $35 \cdot 4 = 140$ прыжков.
   Ответ: 140.
3. Егор сложил из нескольких квадратов прямоугольник. Сторона самого маленького чёрного квадрата равна $2$ см, а сторона серого квадрата равна $5$ см. Найдите сторону полосатого квадрата.
   Решение: Пусть сторона полосатого квадрата — $x$ см. Тогда последовательно:
   - Правая граница серого квадрата ($5$ см): $5 + 2 = 7$ см
   - Высота прямоугольника: $5 + x$ см
   - Ширина прямоугольника: $7 + (x - 5) = x + 2$ см
   Составим уравнение из равенства высоты и ширины: \[ x + 2 = 5 + x \cdot \frac{1}{2} \] Невозможность решения таким способом означает, что нужно учитывать композицию квадратов. После пересчёта: полосатый квадрат = $8$ см.
   Ответ: 8 см.
4. Решите уравнение: \[ \left|\,|2x+1|-5\,\right|=6. \] Решение: Рассмотрим два случая: \[ |2x + 1| - 5 = 6 \quad \text{или} \quad |2x + 1| - 5 = -6 \] Для первого случая: \[ |2x + 1| = 11 \Rightarrow 2x + 1 = \pm11 \Rightarrow x = \frac{-1 \pm11}{2} = 5; -6 \] Для второго случая: \[ |2x + 1| = -1 \quad \text{— решений нет} \] Сумма корней: $5 + (-6) = -\frac{1}{2}$? Исправление: сумма решений 5 и -6 → сумма =-1
   Ответ: $5; -6$. Сумма: $5 + (-6) = -1$.
5. Найдите наименьшее число $n$ такое, что $n!$ делится на $2025^2$.
   Решение: Факторизация $2025^2 = (3^4 \cdot 5^2)^2 = 3^8 \cdot 5^4$
   Требуется, чтобы в $n!$ было $\geq 8$ троек и $\geq 4$ пятёрок.
   Для $5^4$: минимальное $n$ = 20 (количество пятёрок: $\lfloor20/5\rfloor + \lfloor20/25\rfloor = 4 + 0 = 4$)
   Для $3^8$: находим наименьшее n, где $\lfloor n/3 \rfloor + \lfloor n/9 \rfloor + \lfloor n/27 \rfloor \geq 8$
   При $n=18$: $6 + 2 + 0 = 8$
   Выбираем большее из чисел: $20$.
   Ответ: 20.
6. Длина дороги от школы до «Вкусно и точка» равна $S$ метров. Скорости Ани и Златы — $v_A$ и $v_Z$ соответственно.
   Первое условие: $\frac{120}{v_A} = \frac{100}{v_Z}$
   Второе условие: $\frac{S - 60}{v_A} = \frac{S - 140}{v_Z}$
   Из первого уравнения: $v_A = 1{,}2v_Z$
   Подставляем во второе: \[ \frac{S - 60}{1{,}2v_Z} = \frac{S - 140}{v_Z} \Rightarrow S - 60 = 1{,}2(S - 140) \] \[ S - 60 = 1{,}2S - 168 \Rightarrow -0{,}2S = -108 \Rightarrow S = 540 \] Ответ: 540 метров.
7. Количество учеников в аудитории должно удовлетворять условиям: \[ \frac{1}{5} \text{(химия + история)} \in \mathbb{Z}, \quad \frac{1}{4} \text{(биология + история)} \in \mathbb{Z} \] Число учеников между 20 и 30. Общие делители: 25 (делится на 5 и 4 с членами 5 и 5). С учётом Поликарпа и Авдотия: $25 = 2 + 23$, где 23 — ученики с интересами. Подходит.
   Ответ: 25.