Школа № 179 из 6 в 7 класс 2025 год

Школа №179

2025 год

07.03.2025

1. ($1$ балл) Решите уравнение: $4\cdot(0{,}7x-4)-\dfrac{1}{4}=3\cdot(-0{,}2x+6)+1\tfrac{1}{4}$.
2. ($2$ балла) По понедельникам Леша, Дима и Витя после школы вместе идут на кружок. Пока Леша делает $3$ шага, Витя успевает сделать $4$ шага, а Дима $5$ шагов. Известно, что Витя сделал на $179$ шагов больше, чем Леша. Сколько шагов сделал Дима?
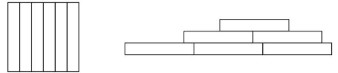
3. ($2$ балла) Алена разрезала квадрат на $6$ равных прямоугольников и сложила из них фигуру, периметр которой равен $51$ см, как показано на рисунке. Найдите периметр исходного квадрата.
   
4. ($2$ балла) Решите уравнение. Если решений несколько, то в ответ запишите их сумму. \[ |3-x|+(x-4)^2=|4-x|^2+1. \]
5. ($2$ балла) Известно, что к $7$ марта $2025$ года на вступительные испытания зарегистрировалось очень много детей. Если бы их зарегистрировалось на $25\%$ меньше, то их было бы $251$ человек. Сколько процентов должно ещё зарегистрироваться (от сегодняшнего количества зарегистрировавшихся), чтобы их стало $493$ человека?
6. ($3$ балла) Папа везёт Капитолину на собеседование в $179$ школу, а живут они далеко. Они проехали за полчаса всего $20$ км и поняли, что если продолжат ехать с той же скоростью, то опоздают на $15$ минут. Тогда папа увеличил скорость на $25\%$, и это позволило Капитолине добраться вовремя. На каком расстоянии в км находится дом Капитолины от $179$ школы?
7. ($3$ балла) Братья Федя и Миша загадали по числу. Известно, что каждое из этих чисел больше $1500$ и меньше $3500$. Миша поделил своё число на $179$ с остатком, и оказалось, что остаток в $5$ раз меньше частного. Федя поделил своё число на $179$ с остатком, и его остаток в $4$ раза меньше частного. Найдите разность этих чисел (считайте, что разность — это неотрицательная величина).

Решения задач

1. Решите уравнение: $4\cdot(0{,}7x-4)-\dfrac{1}{4}=3\cdot(-0{,}2x+6)+1\tfrac{1}{4}$.
   Решение: \[ 4 \cdot (0{,}7x - 4) - \dfrac{1}{4} = 3 \cdot (-0{,}2x + 6) + 1\tfrac{1}{4} \] Преобразуем смешанное число: \[ 1\tfrac{1}{4} = \dfrac{5}{4} \] Раскроем скобки: \[ 2{,}8x - 16 - 0{,}25 = -0{,}6x + 18 + 1{,}25 \] Упростим: \[ 2{,}8x - 16{,}25 = -0{,}6x + 19{,}25 \] Соберём переменные слева, числа справа: \[ 2{,}8x + 0{,}6x = 19{,}25 + 16{,}25 \] \[ 3{,}4x = 35{,}5 \] Решение: \[ x = \dfrac{35{,}5}{3{,}4} = \dfrac{355}{34} = 10\dfrac{15}{34} \] Ответ: $\dfrac{355}{34}$.
2. По понедельникам Леша, Дима и Витя после школы вместе идут на кружок. Пока Леша делает $3$ шага, Витя успевает сделать $4$ шага, а Дима $5$ шагов. Известно, что Витя сделал на $179$ шагов больше, чем Леша. Сколько шагов сделал Дима?
   Решение: Соотношение шагов Леши, Вити и Димы: $3 : 4 : 5$.
   Пусть Леша сделал $3a$ шагов, тогда Витя $4a$, Дима $5a$.
   Разница шагов Вити и Леши: \[ 4a - 3a = 179 \quad \Rightarrow \quad a = 179 \] Шаги Димы: \[ 5a = 5 \cdot 179 = 895 \] Ответ: $895$.
3. Алена разрезала квадрат на $6$ равных прямоугольников и сложила из них фигуру, периметр которой равен $51$ см. Найдите периметр исходного квадрата.
   Решение:
   Пусть длина каждого маленького прямоугольника равна $a$, а его высота равна $b$. По рисунку видно, что при обходе периметра сложенной фигуры суммарная длина всех горизонтальных сторон равна $12a$, а суммарная длина всех вертикальных сторон равна $6b$. Значит, \[ P_{\text{фигуры}} = 12a + 6b. \] По условию $P_{\text{фигуры}} = 51$, поэтому \[ 12a + 6b = 51. \tag{1} \] Исходный квадрат разрезан на $6$ одинаковых прямоугольников. На рисунке слева видно, что квадрат разделён на $6$ одинаковых вертикальных полосок. Если сторона квадрата равна $s$, то высота такой полоски равна $s$, а её ширина равна $\dfrac{s}{6}$. В фигуре справа эти же прямоугольники использованы, только повёрнуты, поэтому \[ a = s, \qquad b = \frac{s}{6}. \] Подставим это в (1): \[ 12s + 6\cdot\frac{s}{6} = 51 \quad\Rightarrow\quad 12s + s = 13s = 51 \quad\Rightarrow\quad s = \frac{51}{13}. \] Периметр исходного квадрата равен \[ P_{\text{кв}} = 4s = 4\cdot\frac{51}{13} = \frac{204}{13}\text{ см}. \] Ответ: $\dfrac{204}{13}$ см.
4. Решите уравнение $|3-x|+(x-4)^2=|4-x|^2+1$. Если решений несколько, то в ответ запишите их сумму.
   Решение: Заметим, что $|4 - x|^2 = (x - 4)^2$, уравнение упрощается: \[ |3 - x| + (x - 4)^2 = (x - 4)^2 + 1 \] Сокращаем $(x - 4)^2$: \[ |3 - x| = 1 \] Решаем уравнение: \[ 3 - x = 1 \quad \vee \quad 3 - x = -1 \] \[ x = 2 \quad \text{или} \quad x = 4 \] Сумма решений: $2 + 4 = 6$. Ответ: $6$.
5. На вступительные испытания зарегистрировалось очень много детей. Если бы их зарегистрировалось на $25\%$ меньше, то их было бы $251$ человек. Сколько процентов должно ещё зарегистрироваться (от сегодняшнего количества зарегистрировавшихся), чтобы их стало $493$ человека?
   Решение: Пусть текущее количество зарегистрированных — $x$.
   Условие при уменьшении на $25\%$: \[ 0{,}75x = 251 \quad \Rightarrow \quad x = \dfrac{251}{0{,}75} = 334\tfrac{2}{3} \] Необходимый прирост до $493$ человек: \[ 493 - 334\tfrac{2}{3} = 158\tfrac{1}{3} \] Процент прироста: \[ \dfrac{158\tfrac{1}{3}}{334\tfrac{2}{3}} \cdot 100% = \dfrac{475}{1004} \cdot 100% \approx 47{,}31\% \] Ответ: $47\tfrac{1}{3}\%$.
6. Папа везёт Капитолину на собеседование в $179$ школу. Они проехали за полчаса $20$ км и поняли, что опоздают на $15$ минут. Увеличив скорость на $25\%$, они добрались вовремя. На каком расстоянии находится дом Капитолины от $179$ школы?
   Решение: Пусть D - все расстояние Оставшееся расстояние — $D - 20$ км. Изначальная скорость $40$ км/ч так как за 30 минут они проезжают 20км.
   Время при исходной скорости: \[ \dfrac{D - 20}{40} = T + 0{,}25 \] После увеличения скорости на $25\%$ до $50$ км/ч: \[ \dfrac{D - 20}{50} = T \] Решение системы уравнений: Подставляем одно в другое \[ \dfrac{D - 20}{40} = \dfrac{D - 20}{50} + 0{,}25 \] \[ \dfrac{D - 20}{40} - \dfrac{D - 20}{50} = 0{,}25 \] Получаем: \[ \dfrac{D - 20}{200} = 0{,}25 \quad \Rightarrow \quad D - 20 = 50 \quad \Rightarrow \quad D = 70 \] Ответ: $70$ км.
7. Братья Федя и Миша загадали по числу от $1500$ до $3500$. Миша поделил своё число на $179$ с остатком, где остаток в $5$ раз меньше частного. Федя поделил своё число на $179$ с остатком, где остаток в $4$ раза меньше частного. Найдите разность этих чисел.
   Решение.
   Пусть Миша загадал число $M$, а Федя — число $F$. В обоих случаях числа делятся на $179$ с остатком. \[ M = 179q_M + r_M,\quad 0 \le r_M < 179, \] \[ F = 179q_F + r_F,\quad 0 \le r_F 3500. \] Значит, возможны два значения: \[ M = 1792 \quad\text{или}\quad M = 2688. \] Для Феди остаток в $4$ раза меньше частного: \[ q_F = 4r_F. \] Тогда \[ F = 179\cdot 4r_F + r_F = (179\cdot 4 + 1)r_F = 717r_F. \] Число $F$ также от $1500$ до $3500$: \[ 1500 \le 717r_F \le 3500. \] Пробуем целые $r_F$: \[ 717\cdot 2 = 1434 3500. \] Значит, возможны два значения: \[ F = 2151 \quad\text{или}\quad F = 2868. \] Переберём все пары $(M,F)$ и найдём разности: \[ |2151 - 1792| = 359, \] \[ |2868 - 1792| = 1076, \] \[ |2688 - 2151| = 537, \] \[ |2868 - 2688| = 180. \] Итак, при данной формулировке задачи возможны следующие значения разности чисел: \[ 180,\ 359,\ 537,\ 1076. \] Ответ: $180$, $359$, $537$, $1076$.