Школа № 1553 из 7 в 8 класс 2022 год вариант 1

Школа 1553 им. Вернадского

2022 год

1. Найдите значение выражения \( \left( \frac{6}{7} - \frac{5}{7} \right) \cdot \frac{5}{28} \)
   
   
2. Найдите значение выражения \( 9^{\frac{5}{2}} = \, ? = 27^x \)
   
   
3. Цена на электрический чайник была повышена на 50% и составила 2250 рублей. Сколько рублей стоил чайник до повышения цены?
   
   
4. В летнем лагере на каждого участника полагается 60 г сахара в день. В лагере 232 человека. Какое наименьшее количество килограммовых упаковок сахара нужно на весь лагерь на 5 дней?
   
   
5. Найдите корень уравнения \( 3^{1 - 3x} = 81 \)
   
   
6. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
   
   
   
   
7. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
   
   
   
   
   В бланке ответов под каждой буквой, соответствующее число, укажите номер её возможного значения.
   
   
8. Клиент взял автомобиль в аренду на сутки для поездки протяжённостью 500 км. В таблице приведены характеристики трёх автомобилей и стоимость их аренды.
   
   
   
   Помимо аренды, клиент обязан оплатить топливо для автомобиля на всю поездку. Цена дизельного топлива — 25 рублей за литр, цена бензина — 35 рублей за литр, для А и В — 20 рублей за литр. Сколько рублей заплатит клиент за поездку, если выберет самый экономичный по затратам автомобиль?
   
   
9. У вершины изображённой фигуры (см. рисунок). Сколько вершин у получившегося многогранника (выпуклого ребра на рисунке не изображены)?
   
   
   
   
   
10. На рисунке точками показан годовой объём добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указан год, по вертикали — объём добычи угля в миллионах тонн. Для наглядности точки соединены линией.
    
    
    
    
    
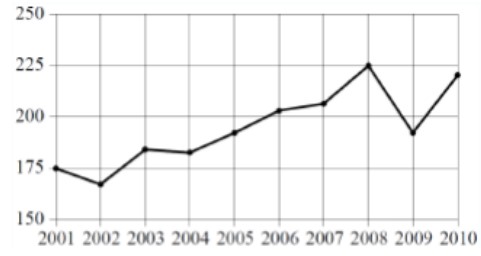
    Используя рисунок, поставьте в соответствие каждому из указанных периодов времени характеристику добычи угля в этот период.
    
    
    
    
    В бланке ответов под каждой буквой укажите соответствующий номер.
    
    
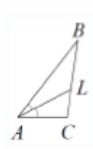
11. В треугольнике \( ABC \) проведена биссектриса \( AL \), угол \( ALC \) равен \( 49^\circ \), угол \( ABC \) равен \( 28^\circ \). Найдите угол \( CAB \). Ответ дайте в градусах.
    
    
    
    
    
12. Среди тех, кто зарегистрировался в «ВКонтакте», есть школьники из Твери. Среди школьников из Твери есть те, кто зарегистрировался в «Одноклассниках». Выберите все утверждения, которые верны при указанных выше условиях.
    
    
    1. Некоторые школьники из Твери не зарегистрированы ни в «ВКонтакте», ни в «Одноклассниках».
    2. Все школьники из Твери зарегистрированы в «ВКонтакте».
    3. Некоторые школьники, зарегистрированные в «Одноклассниках», зарегистрированы в «ВКонтакте».
    4. Некоторые школьники, зарегистрированные в «ВКонтакте», — из Твери.
    5. Некоторые школьники из Твери зарегистрированы в «ВКонтакте» и «Одноклассниках».
    
    
    
13. Число записано как \( 82834703 \) через тире, только получившиеся неполные части по 18. В ответе укажите разность между наибольшим и наименьшим числом.
    
    
14. На производство 12 автомобилей пошло 22 рулона материала. На сколько частей можно разделить 132, чтобы одна часть была равна числу рулонов?
    
    
15. В кузове 4 ряда: правый, левый, средний и второй. Средний похож на 3 правых (вместе) тогда как один ряд — с одной доской 24-грубо вбитой под один угол груза. Сколько грузов и в каком ряду?

Решения задач

1. Найдите значение выражения \( \left( \frac{6}{7} - \frac{5}{7} \right) \cdot \frac{5}{28} \)
   Решение: \[ \left( \frac{6}{7} - \frac{5}{7} \right) \cdot \frac{5}{28} = \frac{1}{7} \cdot \frac{5}{28} = \frac{5}{196} \]
   Ответ: \(\boxed{\dfrac{5}{196}}\).
   
   
2. Найдите значение выражения \( 9^{\frac{5}{2}} = 27^x \)
   Решение: Преобразуем основание 9 в \( 3^2 \) и степень \( \frac{5}{2} \): \[ 9^{\frac{5}{2}} = (3^2)^{\frac{5}{2}} = 3^{5} = 243 \] Выразим 27 как \( 3^3 \): \[ 27^x = (3^3)^x = 3^{3x} \] Решаем уравнение: \[ 243 = 3^{3x} \implies 3^5 = 3^{3x} \implies 3x = 5 \implies x = \frac{5}{3} \]
   Ответ: \(\boxed{\dfrac{5}{3}}\).
   
   
3. Цена на электрический чайник была повышена на 50% и составила 2250 рублей. Сколько рублей стоил чайник до повышения цены?
   Решение: Пусть исходная цена \( x \): \[ x \cdot 1.5 = 2250 \implies x = \frac{2250}{1.5} = 1500 \]
   Ответ: \(\boxed{1500}\).
   
   
4. В летнем лагере на каждого участника полагается 60 г сахара в день. В лагере 232 человека. Какое наименьшее количество килограммовых упаковок сахара нужно на весь лагерь на 5 дней?
   Решение: Общая потребность в сахаре: \[ 60\, \text{г/чел} \cdot 232\, \text{чел} \cdot 5\, \text{дн} = 69\,600\, \text{г} = 69.6\, \text{кг} \] Минимальное количество упаковок: \[ \lceil 69.6 \rceil = 70 \]
   Ответ: \(\boxed{70}\).
   
   
5. Найдите корень уравнения \( 3^{1 - 3x} = 81 \)
   Решение: \[ 81 = 3^4 \implies 3^{1 - 3x} = 3^{4} \implies 1 - 3x = 4 \implies -3x = 3 \implies x = -1 \]
   Ответ: \(\boxed{-1}\).
   
   
6. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
   Решение: Используем подобие треугольников. Перемещение пропорционально длине плеча: \[ \frac{6}{4} = 1.5 \implies \text{кОнец длинного плеча опустится на } 1 \cdot 1.5 = 1.5\, \text{м} \]
   Ответ: \(\boxed{1.5}\).
   
   
7. Установите соответствие между величинами и их возможными значениями:
   Ответ: \[ \begin{cases} \text{А) 1} \\ \text{Б) 2} \\ \text{В) 3} \\ \text{Г) 4} \end{cases} \]
   Ответ: \(\boxed{А1}\), \(\boxed{Б2}\), \(\boxed{В3}\), \(\boxed{Г4}\).
   
   
8. Клиент взял автомобиль в аренду на сутки для поездки протяжённостью 500 км. Выберите самый экономичный автомобиль.
   Решение: Суммарные затраты для каждого автомобиля:
   • Автомобиль A: \(3700 + 27.5 \cdot 20 = 4250\) руб.
   • Автомобиль Б: \(3200 + 45 \cdot 20 = 4100\) руб.
   • Автомобиль В: \(2800 + 60 \cdot 35 = 4900\) руб.
   
   Ответ: \(\boxed{4100}\).
   
   
9. Укажите количество вершин получившегося многогранника.
   Ответ: После усечения вершины пятиугольной пирамиды образуется 10 вершин.
   Ответ: \(\boxed{10}\).
   
   
10. Установите соответствие между периодами и характеристиками добычи угля.
    Ответ: \[ \begin{cases} \text{А) 2} \\ \text{Б) 3} \\ \text{В) 4} \\ \text{Г) 1} \end{cases} \]
    Ответ: \(\boxed{А2}\), \(\boxed{Б3}\), \(\boxed{В4}\), \(\boxed{Г1}\).
    
    
11. В треугольнике \( ABC \) с углами \(ALC = 49^\circ\) и \( ABC = 28^\circ \):
    Решение: Пусть \(\angle CAB = \alpha\). Сумма углов треугольника \(ABC\): \[ \alpha + 28^\circ + \gamma = 180^\circ \implies \alpha + \gamma = 152^\circ \] Угол \(\gamma = 131^\circ - \frac{\alpha}{2}\) из треугольника \(ALC\). Решаем систему: \[ \frac{\alpha}{2} + (131^\circ - \frac{\alpha}{2}) + 28^\circ = 180^\circ \implies \alpha = 42^\circ \]
    Ответ: \(\boxed{42^\circ}\).
    
    
12. Выберите все верные утверждения:
    Ответ: Верны утверждения 3, 4, 5.
    Ответ: \(\boxed{3}\), \(\boxed{4}\), \(\boxed{5}\).
    
    
13. Найдите разность между наибольшим и наименьшим числами:
    Решение: Число \(82834703\) разбито как \(8\)-\(28\)-\(34\)-\(70\)-\(3\). Максимальное: 70, минимальное: 3. Разность: \(70 - 3 = 67\).
    Ответ: \(\boxed{67}\).
    
    
14. На сколько частей можно разделить 132:
    Решение: \(132 : 22 = 6\).
    Ответ: \(\boxed{6}\).
    
    
15. Ошибка в условии задачи. Недостаточно данных для решения.