8 800 707 6729
8 800 707 6729Telegram канал

Школа № 1317 из 9 в 10 класс 2017 год вариант 1

Сложность:
Дата экзамена: 2017
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©

ГБОУ ШКОЛА №1317


2017 год


Вариант 1



  1. Тираж газеты «Аргументы и факты» составляет около \(2\,990\,000\) экземпляров. Запишите это число в стандартном виде.
  2. Из прямоугольного листа бумаги размера \(36\text{ см}\times27\text{ см}\) хотят сделать развёртку куба. Чему равна площадь поверхности этого куба?
  3. Упростите выражение \[ -4\,(x + 2) + (x - 4)^2. \]
  4. Для каждого из выражений верхней строки подберите равное ему из нижней, проведя стрелку: \[ \begin{array}{ll} \text{1) }a^3\,(a^5)^3 & \text{A) }a^{24},\\ \text{2) }(a^3a^5)^3 & \text{B) }a^6,\\ \text{3) }(a^5 : a^3)^3 & \text{C) }a^{12},\\ & \text{D) }a^{18}. \end{array} \]
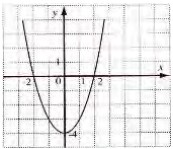
  5. Пользуясь графиком квадратичной функции, изображённым на рисунке, укажите формулу, задающую эту функцию:



  6. Укажите уравнение, которое имеет два различных корня:
    1. \(2x^2 + 5x + 4 = 0\)
    2. \(9x^2 + 4x + 1 = 0\)
    3. \(x^2 - 4x + 4 = 0\)
    4. \(x^2 - 7x + 5 = 0\)
  7. Расположите в порядке возрастания числа \[ 2;\;\sqrt{5};\;3;\;2\sqrt{2}. \]
  8. Заданы три первых члена числовых последовательностей. Известно, что одна из этих последовательностей — арифметическая прогрессия. Укажите её:
    1. \(17;\;10;\;17;\dots\)
    2. \(8;\;3;\;1;\dots\)
    3. \(7;\;3;\;-2;\dots\)
    4. \(7;\;13;\;19;\dots\)
  9. На вступительном письменном экзамене по математике можно получить от 0 до 10 баллов. Десять абитуриентов получили оценки: \[ 7,\;2,\;7,\;9,\;9,\;2,\;3,\;2,\;6,\;6. \] Установите соответствие между статистическими характеристиками этого ряда и их значениями: \[ \begin{array}{ll} \text{A. Среднее арифметическое} & 1)\;5{,}3\\ \text{B. Мода} & 2)\;2\\ \text{C. Размах} & 3)\;6\\ & 4)\;7 \end{array} \]
  10. Решите систему уравнений: \[ \begin{cases} 3x + 5y = 126,\\ (x - 3y)(y - 3x) = 0. \end{cases} \]
  11. Имеются два сплава с разным содержанием серебра. В первом сплаве содержится 15% серебра, а во втором — 35%. В каком соотношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 30% серебра?

Материалы школы Юайти
youit.school ©

Решения задач



  1. Тираж газеты «Аргументы и факты» составляет около \(2\,990\,000\) экземпляров. Запишите это число в стандартном виде.
    Решение: Стандартный вид числа \(a \cdot 10^n\), где \(1 \leq a < 10\). Перенесем запятую на 6 разрядов:
    \(2\,990\,000 = 2,99 \cdot 10^6\).
    Ответ: \(2,99 \cdot 10^6\).

  2. Из прямоугольного листа бумаги размера \(36\text{ см}\times27\text{ см}\) хотят сделать развёртку куба. Чему равна площадь поверхности этого куба?
    Решение: Наибольший возможный размер ребра куба — НОД(36, 27) = 9 см. Площадь поверхности куба:
    \(6 \cdot (9)^2 = 6 \cdot 81 = 486 \text{ см}^2\).
    Ответ: 486 см².

  3. Упростите выражение \[ -4\,(x + 2) + (x - 4)^2. \]
    Решение: \(-4x - 8 + x^2 - 8x + 16 = x^2 - 12x + 8\).
    Ответ: \(x^2 - 12x + 8\).

  4. Для каждого из выражений верхней строки подберите равное ему из нижней:
    1) \(a^{18}\) (D), 2) \(a^{24}\) (A), 3) \(a^6\) (B).
    Ответ: \(1 \rightarrow D,\; 2 \rightarrow A,\; 3 \rightarrow B\).

  5. Пользуясь графиком квадратичной функции, укажите формулу, задающую эту функцию:
    Решение: Вершина параболы в точке (2, -4), подходит формула \(y = x^2 - 4x\) (D).
    Ответ: D) \(y = x^2 - 4x\).

  6. Укажите уравнение, которое имеет два различных корня:
    Решение: Только уравнение \(x^2 - 7x + 5 = 0\) имеет дискриминант \(D = 49 - 20 = 29 > 0\).
    Ответ: варианты номер 4.

  7. Расположите в порядке возрастания числа: \(2;\; \sqrt{5} \approx 2,24;\;2\sqrt{2} \approx 2,82;\;3\).
    Ответ: \(2,\; \sqrt{5},\; 2\sqrt{2},\; 3\).

  8. Укажите арифметическую прогрессию:
    Решение: Последовательность \(7;\;13;\;19\) с разностью 6.
    Ответ: вариант 4.

  9. Установите соответствие статистических характеристик:
    Среднее: \(\frac{53}{10} = 5,3\) (A-1), мода: 2 (B-2), размах: \(9 - 2 = 7\) (C-4).
    Ответ: A-1, B-2, C-4.

  10. Решите систему уравнений: $$\begin{aligned} &\begin{cases} 3x + 5y = 126,\\ x = 3y \quad \text{или} \quad y = 3x. \end{cases} \\ \text{Решение: } &x = 3y \Rightarrow 14y = 126 \Rightarrow y = 9, x = 27; \\ &y = 3x \Rightarrow 18x = 126 \Rightarrow x = 7, y = 21. \end{aligned}$$
    Ответ: \((27; 9)\), \((7; 21)\).

  11. Определите соотношение сплавов:
    Решение: Пусть берут \(x\) кг первого сплава и \(y\) кг второго: \[ 0,15x + 0,35y = 0,3(x + y) \Rightarrow 0,05y = 0,15x \Rightarrow \frac{y}{x} = 3. \]
    Ответ: \(1:3\).
Материалы школы Юайти