Школа № 109 из 8 в 9 класс 2023 год вариант 1-1
Печать
youit.school ©
Школа № 109 Ямбурга
2023 год
- Найдите значение выражения:
- \( 6^{-2} - \left( \dfrac{12}{5} \right)^{-1} \)
- \( \dfrac{7^{-8} \cdot 7^{-9}}{7^{-16}} \)
- \( \dfrac{16^{-5} \cdot (-64)^{-3}}{256^{-4}} \)
- Найдите значение выражения:
\[
\frac{26}{4 - \sqrt{3}} - \frac{5}{3 + 2\sqrt{2}} - \sqrt{2}(10 + \sqrt{6})
\]
Ответ: $\rule{5cm}{0.4pt}$
- Решите уравнение:
\[
3x^2 - 192 = 0
\]
Ответ: $\rule{5cm}{0.4pt}$
- Решите уравнение:
\[
x^2 - 7x + 6 = 0
\]
Ответ: $\rule{5cm}{0.4pt}$
- Решите уравнение:
\[
\frac{3x^2 - 5x - 2}{2 - x} = 0
\]
Ответ: $\rule{5cm}{0.4pt}$
- Решите задачу:
Через две трубы бассейн наполняется водой за 5 часов.
Сколько времени потребовалось бы для наполнения бассейна только через первую трубу,
если через неё бассейн заполняется на 24 часа быстрее, чем через вторую?
Ответ: $\rule{5cm}{0.4pt}$
- Решите графически уравнение:
\[
\frac{4}{x} = \frac{x}{2} - 1
\]
Ответ: $\rule{5cm}{0.4pt}$
-
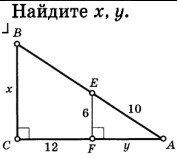
Ответ: $\rule{5cm}{0.4pt}$
-
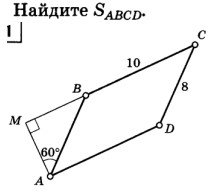
Ответ: $\rule{5cm}{0.4pt}$
-
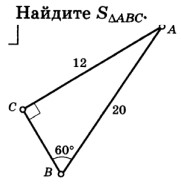
Ответ: $\rule{5cm}{0.4pt}$
-
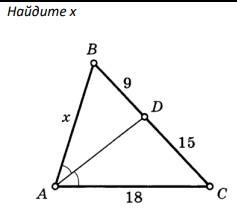
Ответ: $\rule{5cm}{0.4pt}$
-
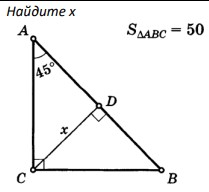
Ответ: $\rule{5cm}{0.4pt}$
-
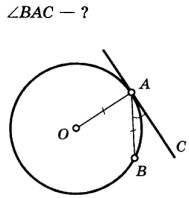
Ответ: $\rule{5cm}{0.4pt}$
-
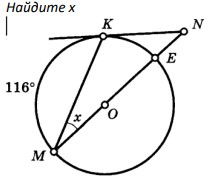
Ответ: $\rule{5cm}{0.4pt}$
Материалы школы Юайти
youit.school ©
Решения задач
-
- Найдите значение выражения: \( 6^{-2} - \left( \dfrac{12}{5} \right)^{-1} \)
Решение: \[ 6^{-2} = \frac{1}{6^2} = \frac{1}{36}; \quad \left( \frac{12}{5} \right)^{-1} = \frac{5}{12} \] \[ \frac{1}{36} - \frac{5}{12} = \frac{1}{36} - \frac{15}{36} = -\frac{14}{36} = -\frac{7}{18} \] Ответ: \(-\dfrac{7}{18}\). - Найдите значение выражения: \( \dfrac{7^{-8} \cdot 7^{-9}}{7^{-16}} \)
Решение: \[ \frac{7^{-8} \cdot 7^{-9}}{7^{-16}} = 7^{-8 + (-9) - (-16)} = 7^{-1} = \frac{1}{7} \] Ответ: \(\dfrac{1}{7}\). - Найдите значение выражения: \( \dfrac{16^{-5} \cdot (-64)^{-3}}{256^{-4}} \)
Решение: \[ 16 = 2^4, \quad 64 = 2^6, \quad 256 = 2^8 \] \[ \frac{(2^4)^{-5} \cdot (-2^6)^{-3}}{(2^8)^{-4}} = \frac{2^{-20} \cdot (-1)^{-3} \cdot 2^{-18}}{2^{-32}} = \frac{-2^{-38}}{2^{-32}} = -2^{-6} = -\frac{1}{64} \] Ответ: \(-\dfrac{1}{64}\).
- Найдите значение выражения: \( 6^{-2} - \left( \dfrac{12}{5} \right)^{-1} \)
- Найдите значение выражения: \[ \frac{26}{4 - \sqrt{3}} - \frac{5}{3 + 2\sqrt{2}} - \sqrt{2}(10 + \sqrt{6}) \] Решение: \[ \frac{26}{4 - \sqrt{3}} = \frac{26(4 + \sqrt{3})}{(4)^2 - (\sqrt{3})^2} = \frac{26(4 + \sqrt{3})}{13} = 2(4 + \sqrt{3}) = 8 + 2\sqrt{3} \] \[ \frac{5}{3 + 2\sqrt{2}} = \frac{5(3 - 2\sqrt{2})}{(3)^2 - (2\sqrt{2})^2} = \frac{5(3 - 2\sqrt{2})}{1} = 15 - 10\sqrt{2} \] \[ \sqrt{2}(10 + \sqrt{6}) = 10\sqrt{2} + \sqrt{12} = 10\sqrt{2} + 2\sqrt{3} \] Собираем все части: \[ (8 + 2\sqrt{3}) - (15 - 10\sqrt{2}) - (10\sqrt{2} + 2\sqrt{3}) = 8 - 15 + 2\sqrt{3} - 2\sqrt{3} + 10\sqrt{2} - 10\sqrt{2} = -7 \] Ответ: \(-7\).
- Решите уравнение: \(3x^2 - 192 = 0\)
Решение: \[ 3x^2 = 192 \quad \Rightarrow \quad x^2 = 64 \quad \Rightarrow \quad x = \pm 8 \] Ответ: \(8; -8\). - Решите уравнение: \(x^2 - 7x + 6 = 0\)
Решение: \[ D = 49 - 24 = 25; \quad x = \frac{7 \pm 5}{2} \quad \Rightarrow \quad x_1 = 6, \quad x_2 = 1 \] Ответ: \(6; 1\). - Решите уравнение: \(\frac{3x^2 - 5x - 2}{2 - x} = 0\)
Решение: Числитель равен нулю: \[ 3x^2 - 5x - 2 = 0; \quad D = 25 + 24 = 49; \quad x = \frac{5 \pm 7}{6} \] \[ x_1 = 2 \quad (\text{не подходит, так как знаменатель 0}), \quad x_2 = -\frac{1}{3} \] Ответ: \(-\dfrac{1}{3}\). - Решите задачу:
Через две трубы бассейн наполняется водой за 5 часов.
Сколько времени потребовалось бы для наполнения бассейна только через первую трубу,
если через неё бассейн заполняется на 24 часа быстрее, чем через вторую?
Решение: Пусть первая труба заполняет за \(t\) часов, тогда вторая за \(t + 24\) часов: \[ \frac{1}{t} + \frac{1}{t + 24} = \frac{1}{5} \] \[ \frac{2t + 24}{t(t + 24)} = \frac{1}{5} \quad \Rightarrow \quad t^2 + 14t - 120 = 0 \] \[ D = 196 + 480 = 676; \quad t = \frac{-14 + 26}{2} = 6 \] Ответ: \(6\) часов. - Решите графически уравнение: \(\frac{4}{x} = \frac{x}{2} - 1\)
Решение: Умножим обе части на \(2x\): \[ 8 = x^2 - 2x \quad \Rightarrow \quad x^2 - 2x - 8 = 0 \] \[ D = 4 + 32 = 36; \quad x = \frac{2 \pm 6}{2} \quad \Rightarrow \quad x_1 = 4, \quad x_2 = -2 \] Ответ: \(4; -2\). - Задачи с 8 по 14 требуют визуального анализа изображений, которые отсутствуют. Для их решения необходимы условия, представленные на рисунках.
Материалы школы Юайти