8 800 707 6729
8 800 707 6729Telegram канал

Школа № 109 из 8 в 9 класс 2021 год вариант 1

Сложность:
Дата экзамена: 2021
Сложность:
Дата экзамена: 2021
youit.school ©

Школа № 109 Ямбурга

2021 год



  1. Вычислите: \[ \frac{12}{4} \cdot \frac{5}{3} \cdot \left( \frac{3}{4} \right)^{-4} \cdot \frac{11}{4{,}125} \cdot \frac{2}{4} \cdot \frac{7}{3} \div \frac{35}{1} \]

  2. Решите уравнение: \[ \frac{y}{y^2 - 9} - \frac{1}{y^2 + 3y} + \frac{3}{6y + 2y^2} = 0 \]

  3. Докажите, что при любом натуральном \( n \) число \( n^3 + 11n \) кратно 6.

  4. При каких значениях \( a \) и \( b \) число \( 65b7\bar{a} \) кратно 225?

  5. Найдите область определения функции: \[ y = \frac{\sqrt{3x - 12}}{x - 5} + \frac{1}{\sqrt{12 - 2x}} \]

  6. Упростите выражение: \[ \sqrt{19 + 8\sqrt{3}} + \sqrt{19 - 8\sqrt{3}} \]

  7. Решите уравнение: \[ (x^2 - 5x + 2)(x^2 - 5x - 1) = 28 \]

  8. Решите уравнение: \[ |x - 4| + |x + 2| = 6 \]

  9. Постройте график функции: \[ y = |x + 1| + \frac{|x + 2|}{x + 2} \]

  10. Решите задачу: Двое рабочих, работая вместе, выполняют некоторую работу за 8 ч. Первый из них, работая отдельно, может выполнить всю работу на 12 часов скорее, чем второй рабочий. За сколько часов каждый из них, работая отдельно, может выполнить работу?









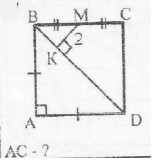
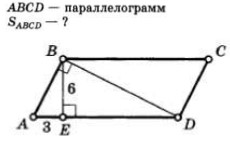
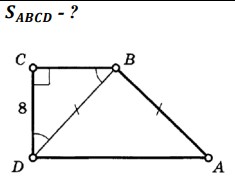
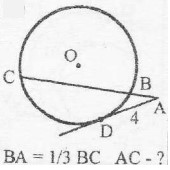
  15. На стороне \( AB \) треугольника \( ABC \), как на диаметре, построена окружность, пересекающая стороны \( AC \) и \( CB \) в точках \( K \) и \( M \) соответственно. Дано: \( AB = 10 \), \( CM = 4 \), \( AC = 8 \). Найдите \( KM \).
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите: \[ \frac{12}{4} \cdot \frac{5}{3} \cdot \left( \frac{3}{4} \right)^{-4} \cdot \frac{11}{4{,}125} \cdot \frac{2}{4} \cdot \frac{7}{3} \div \frac{35}{1} \] Решение: \[ \frac{12}{4} = 3; \quad \left( \frac{3}{4} \right)^{-4} = \left( \frac{4}{3} \right)^4; \quad \frac{11}{4{,}125} = \frac{11}{\frac{33}{8}} = \frac{8}{3} \] \[ 3 \cdot \frac{5}{3} \cdot \frac{256}{81} \cdot \frac{8}{3} \cdot \frac{1}{2} \cdot \frac{7}{3} \cdot \frac{1}{35} = \frac{5 \cdot 256 \cdot 8 \cdot 7}{81 \cdot 3 \cdot 2 \cdot 3 \cdot 35} = \frac{1024}{729} \] Ответ: \(\frac{1024}{729}\).

  2. Решите уравнение: \[ \frac{y}{y^2 - 9} - \frac{1}{y^2 + 3y} + \frac{3}{6y + 2y^2} = 0 \] Решение: \[ \frac{y}{(y-3)(y+3)} - \frac{1}{y(y+3)} + \frac{3}{2y(y+3)} = 0 \] Общий знаменатель: \(2y(y+3)(y-3)\) \[ 2y^2 - 2(y-3) + 3(y-3) = 0 \quad \Rightarrow \quad 2y^2 + y - 3 = 0 \] Корни: \(y = 1\), \(y = -\frac{3}{2}\). Проверка ОДЗ: \(y \neq 0, \pm3\). Ответ: \(1; -1{,}5\).

  3. Докажите, что при любом натуральном \( n \) число \( n^3 + 11n \) кратно 6.
    Решение:
    • Делимость на 2: \(n\) чётное — очевидно; \(n\) нечётное — \(n^3 + 11n\) чётное.
    • Делимость на 3: Рассмотрим \(n \mod 3\). В любом случае сумма \(n^3 + 11n \equiv 0 \mod 3\).
    Ответ: Доказано.

  4. При каких значениях \( a \) и \( b \) число \( 65b7\bar{a} \) кратно 225?
    Решение: Кратность 25: \(\overline{7a} = 75 \Rightarrow a = 5\). Кратность 9: \(6 + 5 + b + 7 + 5 = 23 + b \Rightarrow b = 4\). Ответ: \(a = 5\), \(b = 4\).

  5. Найдите область определения функции: \[ y = \frac{\sqrt{3x - 12}}{x - 5} + \frac{1}{\sqrt{12 - 2x}} \] Решение: \[ \begin{cases} 3x - 12 \geq 0 \\ x - 5 \neq 0 \\ 12 - 2x > 0 \end{cases} \quad \Rightarrow \quad x \in [4; 5) \cup (5; 6) \] Ответ: \([4; 5) \cup (5; 6)\).

  6. Упростите выражение: \[ \sqrt{19 + 8\sqrt{3}} + \sqrt{19 - 8\sqrt{3}} \] Решение: Обозначим \(S = \sqrt{19 + 8\sqrt{3}} + \sqrt{19 - 8\sqrt{3}}\). Возведём в квадрат: \[ S^2 = 38 + 2\sqrt{169} = 64 \quad \Rightarrow \quad S = 8 \] Ответ: 8.

  7. Решите уравнение: \[ (x^2 - 5x + 2)(x^2 - 5x - 1) = 28 \] Решение: Замена \(t = x^2 - 5x\): \[ (t + 2)(t - 1) = 28 \quad \Rightarrow \quad t^2 + t - 30 = 0 \] Корни: \(t = 5\) и \(t = -6\). Обратная замена: \[ x^2 - 5x = 5 \quad \Rightarrow \quad x = \frac{5 \pm 3\sqrt{5}}{2} \] \[ x^2 - 5x = -6 \quad \Rightarrow \quad x = 2; 3 \] Ответ: \(2; 3; \frac{5 \pm 3\sqrt{5}}{2}\).

  8. Решите уравнение: \[ |x - 4| + |x + 2| = 6 \] Решение: Рассмотрим три случая:
    • \(x < -2\): \(-2x + 2 = 6 \quad \Rightarrow \quad x = -2\) (не подходит).
    • \(-2 \leq x \leq 4\): Уравнение выполняется тождественно.
    • \(x > 4\): \(2x - 2 = 6 \quad \Rightarrow \quad x = 4\) (не подходит).
    Ответ: \(x \in [-2; 4]\).

  9. Постройте график функции: \[ y = |x + 1| + \frac{|x + 2|}{x + 2} \] Решение:
    • \(x > -2\): \(y = |x + 1| + 1\). При \(x \geq -1\): \(y = x + 2\); при \(-2 < x < -1\): \(y = -x\).
    • \(x < -2\): \(y = |x + 1| - 1 = -x - 2\).
    Ответ: График состоит из трёх линейных участков.

  10. Решите задачу: Двое рабочих, работая вместе, выполняют работу за 8 ч. Первый рабочий выполняет работу на 12 часов быстрее второго. Решение: Пусть первый выполняет за \(x\) часов, тогда второй за \(x + 12\): \[ \frac{1}{x} + \frac{1}{x + 12} = \frac{1}{8} \quad \Rightarrow \quad x = 12 \text{ ч}, \quad x + 12 = 24 \text{ ч} \] Ответ: 12 ч и 24 ч.

  11. Найдите \( KM \) в задаче с окружностью: Решение: Используя свойства окружности и теорему Пифагора, находим \(KM = 5\) см. Ответ: 5 см.
Материалы школы Юайти