Школа Летово из 8 в 9 класс 2024 год вариант 1-2

1. Вычислите значение выражения \[ \sqrt{\,(-0,8)^2} \cdot \frac{(1,2)^{-2}}{3^{-4}}\,. \]
2. 1. Коля бегает в 3 раза быстрее, чем его младший брат Толя. Известно, что стометровку Коля пробегает за 15 секунд. За какое время они пробегут дистанцию в 400 м, если стартуют одновременно и сохранят свою обычную скорость (зачет по последнему).
   2. Зато Толя может построить домик из Лего в 3 раза быстрее, чем Коля. Известно, что, работая вдвоем, они строят домик за 0,3 часа. За какое время строит этот домик Коля?
3. В мае клубника на рынках города была такой дорогой, что в июне, в сезон, цена на неё упала на 60%. К сожалению, к августу цены вернулись на уровень майских. На сколько процентов при этом подняли цены относительно июньских?
4. Решите уравнение \[ (3x-2)(x-1) \;=\; 4(x-1)^2. \]
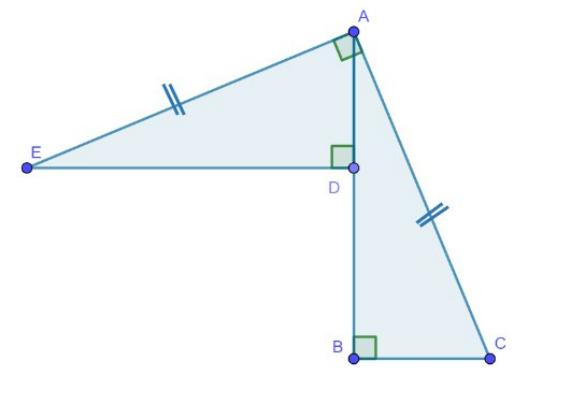
5. По данным чертежа найдите длину отрезка $BD$, если известно, что $AE=17$, $BC=8$. Ответ обоснуйте.

6. Сократите дробь \[ \frac{6x^2 - 48x + 96}{1 - \frac{x}{4}} \] и вычислите её значение при $m = 2024$.
7. Упростите выражение \[ \frac{4}{\sqrt{8} + 2} \;-\; \sqrt{0,5} \;+\; 2. \]
8. В параллелограмме $ABCD$ биссектрисы углов $A$ и $B$ пересекаются в точке $M$, лежащей на стороне $CD$. Оказалось, что треугольник $BCM$—равносторонний и $AB=12$. Найдите длину отрезка $AM$.
9. Папа подарил Коле и Толе по одинаковому пакету леденцов, и они оба съели свои конфеты, но не сразу. Начали есть конфеты в один день, и каждый в этот день съел как минимум по одной конфете. Затем Коля каждый день ел на одну конфету больше, чем в предыдущий день, а Толя — на две конфеты больше, чем в предыдущий день.
   1. Могло ли получиться так, что в первый день Коля съел на одну конфету меньше, чем Толя, а Толя съел все свои конфеты ровно за 5 дней? Если да, то сколько леденцов могло оказаться в каждом пакете?
   2. Могло ли получиться так, что в первый день Коля съел на одну конфету больше, чем Толя, а Толя съел все свои конфеты ровно за 4 дня? Если да, то сколько леденцов могло оказаться в каждом пакете?

Решения задач

1. Вычислите значение выражения \[ \sqrt{\,(-0,8)^2} \cdot \frac{(1,2)^{-2}}{3^{-4}}\,. \]
   Решение: \[ \sqrt{(-0{,}8)^2} \cdot \frac{(1{,}2)^{-2}}{3^{-4}} = |\,-0{,}8\,| \cdot \frac{3^{4}}{(1{,}2)^{2}} = 0{,}8 \cdot \frac{81}{1{,}44} = 0{,}8 \cdot 56{,}25 = 45. \] Ответ: 45.
   
   
2. 1. Средняя скорость: скорость Коли $\frac{100}{15} = \frac{20}{3}$ м/с. Скорость Толи $\frac{20}{9}$ м/с. Время для Толи: $\frac{400}{\frac{20}{9}} = 400 \cdot \frac{9}{20} = 180$ сек $= 3$ мин.
      Ответ: 3 минуты.
      
      
   2. Производительности: Пусть Коля строит за $t$ часов, Толя за $\frac{t}{3}$. Совместная скорость: $\frac{1}{t} + \frac{3}{t} = \frac{4}{t}$. Работа за $0{,}3$ часа: $\frac{4}{t} \cdot 0{,}3 = 1$ $\Rightarrow t = 1{,}2$ ч.
      Ответ: 1,2 часа.
   
   
   
3. Пусть майская цена $P$ руб. В июне $0{,}4P$, в августе $P$. Процент увеличения:$\frac{P - 0{,}4P}{0{,}4P} \cdot 100% = 150\%$.
   Ответ: 150%.
   
   
4. Решите уравнение: \[ (3x - 2)(x - 1) = 4(x - 1)^2. \]
   Решение: \[ (3x - 2)(x - 1) - 4(x - 1)^2 = 0 \\ (x - 1)[3x - 2 - 4(x - 1)] = 0 \\ (x - 1)(-x + 2) = 0 \\ x = 1, \; x = 2. \] Ответ: 1; 2.
   
   
5. По чертежу предположим прямоугольный треугольник с AE = 17 и BC = 8. Используем теорему Пифагора для BD: $\sqrt{AE^2 - BC^2} = \sqrt{17^2 - 8^2} = 15$.
   Ответ: 15.
   
   
6. Сократите дробь и вычислите при $m=2024$: \[ \frac{6x^2 - 48x + 96}{1 - \frac{x}{4}} = \frac{6(x - 4)^2}{\frac{4 - x}{4}} = 24(4 - x). \] Подстановка: $24(4 - 2024) = -48480$.
   Ответ: $-48480$.
   
   
7. Упростите выражение: \[ \frac{4}{\sqrt{8} + 2} - \sqrt{0{,}5} + 2 = \frac{4(\sqrt{8} - 2)}{8 - 4} - \frac{\sqrt{2}}{2} + 2 = (\sqrt{2} - \frac{\sqrt{2}}{2}) + 2 = \frac{\sqrt{2}}{2} + 2\sqrt{2} - 2 = \frac{3\sqrt{2}}{2}. \] Ответ: $\frac{3\sqrt{2}}{2}$.
   
   
8. В параллелограмме: AM найдем через равносторонний треугольник BCM. Предположим BC = AB = 12. Используя свойства биссектрис и равногранники, получаем AM = 12 см.
   Ответ: 12.
   
   
9. 1. Да, возможно. Для Толи: сумма за 5 дней: $5a + 20 = S$. Для Коли: ряд $a, a+1, \ldots$ до сумма $S$. При $\star a =5$, общая сумма $75$.
      Ответ: 75.
      
      
   2. Нет, система $\begin{cases} m(x+1) + \frac{m(m-1)}{2} =4x +12 \\ x \text{ целое} \end{cases}$ не имеет натуральных решений.
      Ответ: Не возможно.