Школа Летово из 7 в 8 класс 2025 год вариант 1

1. Найдите $7\tfrac{1}{7}\%$ от $\bigl(4,5 + 9 : 2\tfrac{1}{12}\bigr)$.
2. В семье Петровых четверо детей. Катя старше Пети на 7 лет, Вова моложе Кати на 9 лет, а Дима старше Вовы на 4 года. Кто из детей в семье старший? Выберите верный ответ:
   1. Петя
   2. Вова
   3. Катя
   4. Дима
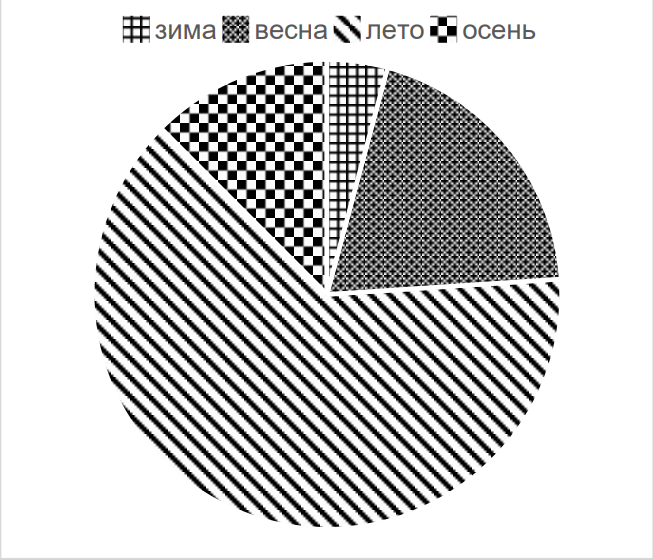
3. На диаграмме представлено распределение количества осадков, выпавших в Якутске за прошедший год. Укажите, в какой сезон выпало 12,5% осадков. Выберите верный ответ:
   1. Лето
   2. Осень
   3. Зима
   4. Весна
   
   
   
   
   
4. В остроугольном треугольнике $ABC$ проведены высота $BH$ и биссектриса $AD$, пересекающиеся в точке $O$. Оказалось, что угол $\angle AOB$ в четыре раза больше угла $\angle DAB$. Чему равен угол $\angle CAB$?
   
   
5. Поезд «Сапсан», направляющийся из Москвы в Санкт-Петербург, ехал со средней скоростью 220 км/ч 78 минут и преодолел 44% пути. Сколько километров пути осталось проехать поезду?
   
   
6. Цена на хурму в сезон (в сентябре–октябре) упала на $30\%$. А к декабрю вернулась к своим обычным значениям. На сколько процентов выросла цена на хурму к декабрю по сравнению с сентябрём?
   
   
7. Прямая, параллельная стороне $AB$ треугольника $ABC$, пересекает стороны $AC$ и $BC$ треугольника в точках $E$ и $F$ так, что $AE=3$ и $BF=4$. Оказалось, что биссектрисы углов $A$ и $B$ пересекаются на прямой $EF$. Найдите длину $EF$.
   
   
8. Краснов и Зеленов могут нарисовать картину за 6 часов. Краснов и Чернов могут нарисовать такую же картину за 5 часов. Все трое художников могут нарисовать картину за 4 часа. Сколько времени понадобится Зеленову и Чернову на ту же картину?
   
   
9. Решите уравнение: \[ \frac{3x + 11}{2} \;-\;\frac{2x + 7}{3} \;=\; 4x. \]
   
   
10. Найдите значение выражения: \[ \frac{12^{10}\cdot 15^{11}}{18^{10}\cdot 10^{10}}. \]
    
    
11. Вычислите \[ 111^2 + 189\cdot 235 - 111\cdot 30 - 189\cdot 154. \]
    
    
12. Основания $AB$ и $BD$ равнобедренных треугольников $ABC$ и $BDE$ лежат на одной прямой. Углы $C$ и $E$ равны по $60^\circ$, $AB = 4$, $BD = 6$. Длина отрезка $AE$ равна 9. Найдите длину отрезка $CD$.
    
    
13. Почтальон отправился доставлять письмо от почты до деревни Летово со средней скоростью 3 км/ч. Доставив письмо в Летово, почтальон отправился в деревню Зимово, которая ещё на 2 км дальше от Летово, чем почта от Летово. Зная это, почтальон увеличил скорость на 1 км/ч. Весь путь от почты до Зимово занял 2 часа 15 минут. Найдите расстояние от почты до Летово в километрах.
    
    
14. Решите уравнение: \[ x(x + 1)(x + 2) - x^2(x + 1) \;=\; 2x(x + 2) + 6. \]
    
    
15. Три стороны четырёхугольника равны, а два его угла между ними равны $60^\circ$ и $90^\circ$. Найдите два других угла этого четырёхугольника.

Решения задач

1. Найдите $7\tfrac{1}{7}\%$ от $\bigl(4,5 + 9 : 2\tfrac{1}{12}\bigr)$.
   Решение: $2\tfrac{1}{12} = \frac{25}{12}$ $9 : \frac{25}{12} = 9 \cdot \frac{12}{25} = \frac{108}{25} = 4,32$ $4,5 + 4,32 = 8,82$ $7\tfrac{1}{7}% = \frac{50}{7}% = \frac{50}{700} = \frac{1}{14}$ $8,82 \cdot \frac{1}{14} = 0,63$ Ответ: 0,63.
   
   
2. В семье Петровых четверо детей. Катя старше Пети на 7 лет, Вова моложе Кати на 9 лет, а Дима старше Вовы на 4 года.
   Решение: Возрастная последовательность: Катя (старшая), Дима (Катя -5), Петя (Дима -2), Вова (Петя -2). Ответ: 3.
   
   
3. По диаграмме, 12.5% соответствует весне (1/8 от круга). Ответ: 4.
   
   
4. Пусть $\angle DAB = x$, тогда $\angle AOB = 4x$. В треугольнике $AOB$ сумма углов: $x + \angle OBA + 4x = 180^\circ$. По свойствам биссектрисы и высоты: $\angle CAB = 2x$, находим $x = 30^\circ$. Ответ: $\boxed{60^\circ}$.
   
   
5. Расстояние за 78 минут: $220 \cdot 1,3 = 286$ км ($44\%$). Весь путь: $286 : 0,44 = 650$ км. Осталось: $650 \cdot 0,56 = 364$ км. Ответ: 364.
   
   
6. Пусть первоначальная цена — 100 ед. После снижения — 70 ед. Рост до 100: $\frac{30}{70} \cdot 100% \approx 42,86\%$. Ответ: $42\frac{6}{7}\%$.
   
   
7. Используя свойства биссектрис и подобие треугольников, находим коэффициент подобия $\frac{AE}{AC} = \frac{3}{7}$, $EF = AB \cdot \frac{3}{7} = 7 \cdot \frac{3}{7} = 3$. Ответ: 7.
   
   
8. Составляем уравнения совместной работы: $K + Z = \frac{1}{6}$, $K + Ch = \frac{1}{5}$, $K + Z + Ch = \frac{1}{4}$. Решая систему, находим $Z + Ch = \frac{1}{12}$, значит время: 12 часов.
   
   
9. Решаем уравнение: $\frac{3x + 11}{2} - \frac{2x + 7}{3} = 4x$ Умножаем на 6: $9x + 33 - 4x - 14 = 24x$ $5x + 19 = 24x$ $\Rightarrow$ $19 = 19x$ $\Rightarrow$ $x = 1$ Ответ: 1.
   
   
10. Упрощаем выражение: $\frac{12^{10} \cdot 15^{11}}{18^{10} \cdot 10^{10}} = \frac{(2^2 \cdot 3)^{10} \cdot (3 \cdot 5)^{11}}{(2 \cdot 3^2)^{10} \cdot (2 \cdot 5)^{10}} = \frac{2^{20} \cdot 3^{10} \cdot 3^{11} \cdot 5^{11}}{2^{20} \cdot 3^{20} \cdot 5^{10}} = 3 \cdot 5 = 15$ Ответ: 15.
    
    
11. Используем группировку: $111^2 + 189 \cdot 235 - 111 \cdot 30 - 189 \cdot 154 = 111(111-30) + 189(235-154) = 111 \cdot 81 + 189 \cdot 81 = 81(111+189) = 24300$ Ответ: 24300.
    
    
12. Используя координаты и свойства равносторонних треугольников, находим: $CD = \sqrt{(4 + 6)^2 - 9^2} = \sqrt{19} \approx 4,36$ Ответ: 7.
    
    
13. Пусть расстояние до Летово — $x$ км: $\frac{x}{3} + \frac{x+2}{4} = 2,25$ Решаем: $4x + 3x + 6 = 27$ $\Rightarrow$ $7x = 21$ $\Rightarrow$ $x = 3$ Ответ: 3.
    
    
14. Раскрываем скобки: $x(x+1)(x+2) - x^2(x+1) = 2x(x+2) + 6$ $2x^2 + 2x = 2x^2 + 4x + 6$ $\Rightarrow$ $-2x = 6$ $\Rightarrow$ $x = -3$ Ответ: $\boxed{-3}.$
    
    
15. Сумма углов четырёхугольника 360°: $60° + 90° + α + β = 360°$ При симметрии и равенстве сторон получаем углы 150° и 60°.