Школа Летово из 7 в 8 класс 2024 год вариант 1

1. Вычислите: \[ \frac{(-5)^5\cdot(-5)^{14}}{(5^3)^6}. \]
2. В четырёхугольнике \(ABCD\); \(AB = AD\) и \(BC \parallel AD\). Найдите \(\angle BAD\), если \(\angle BCD = 112^\circ\) и \(\angle BDC = 8^\circ\).
3. Решите уравнение: \[ 2x(x-1) - (2x+3)(x-1) = 4(3-2x). \]
4. Саша неожиданно уехала в командировку и оставила своего кота Тортика подруге Асе. У Аси тоже есть кошка. И запасы кошачьей еды. Асииной кошке этих запасов хватит на 9 дней, а Тортику только на 7. Хватит ли им двоим этого корма хотя бы на те четыре дня, которые Тортик должен прожить у Аси? Ответ обсудите.
5. Вычислите: \[ \frac{\bigl(97\tfrac{4}{15} - 95\tfrac{5}{18}\bigr)\,\cdot\,2\tfrac{1}{4} + 0,373}{0,3} \;:\;\frac{2}{3}. \]
6. В четырёхугольнике \(ABCD\); \(AB = BC\), \(AD = CD\). Докажите, что диагонали этого четырёхугольника перпендикулярны.
7. Три грибника Сыроежкин, Опяткин и Лисичкин сложили собранные ими грибы в одну корзину и взвесили её. Весы показали 8 кг. Сыроежкин похвастался, что собранные им грибы составляют 35% всех грибов. Опяткин в ответ сказал, что собранные Сыроежкиным грибы составляют всего лишь 87,5% от грибов, собранных самим Опяткиным. Лисичкин промолчал. На сколько процентов грибов больше собрал Сыроежкин, чем Лисичкин?
8. У семи нянек есть 30 булочек — с маком, с корицей и булочки без ничего, всех булочек поровну. Первая няня взяла две булочки с маком и три булочки с корицей — всего на 600 граммов. Вторая няня взяла четыре булочки с маком и одну булочку без ничего — всего на 350 граммов. Третья няня взяла три булочки с корицей и пять без ничего — у неё получилось 700 граммов. Остальные няни забрали себе оставшиеся булочки поровну. Сколько весили булочки, которые взяла седьмая няня?
9. В равнобедренном треугольнике \(ABC\) с основанием \(BC\) провели высоты \(BE\) и \(CF\) и отметили точку их пересечения \(H\).
   1. Найдите величину угла \(ACF\), если величина угла \(BAC\) равна \(40^\circ\).
   2. Найдите угол \(BHC\).
   3. Докажите, что треугольник \(BCH\) равнобедренный.
   4. Сторону \(AB\) этого треугольника продлили за точку \(A\) и отметили точку \(K\) так, что \(AB = AK\). Найдите величину угла \(KCB\), если величина угла \(BAC\) известна. Данные занесите в таблицу:
      
      Сформулируйте замеченную закономерность и докажите её.

Решения задач

1. Вычислите: \(\frac{(-5)^5 \cdot (-5)^{14}}{(5^3)^6}\)
   Решение:
   Используем свойства степеней: \[ \frac{(-5)^5 \cdot (-5)^{14}}{(5^3)^6} = \frac{(-5)^{19}}{5^{18}} = (-5)^{19-18} = -5 \] Ответ: \(-5\).
   
   
2. В четырёхугольнике \(ABCD\) \; \(AB = AD\) и \(BC \parallel AD\). Найдите \(\angle BAD\), если \(\angle BCD = 112^\circ\) и \(\angle BDC = 8^\circ\).
   Решение:
   В треугольнике \(BCD\): \[ \angle CBD = 180^\circ - 112^\circ - 8^\circ = 60^\circ \] Так как \(BC \parallel AD\), \(\angle BDA = \angle CBD = 60^\circ\). В треугольнике \(ABD\) (\(AB = AD\)): \[ \angle ABD = \angle ADB = 60^\circ \implies \angle BAD = 180^\circ - 2 \cdot 60^\circ = 60^\circ \] Ответ: \(60^\circ\).
   
   
3. Решите уравнение: \(2x(x-1) - (2x+3)(x-1) = 4(3-2x)\)
   Решение:
   Раскроем скобки и упростим: \[ 2x^2 - 2x - (2x^2 + x - 3) = 12 - 8x \implies -3x + 3 = 12 - 8x \implies 5x = 9 \implies x = \frac{9}{5} \] Ответ: \(\frac{9}{5}\).
   
   
4. Определите, хватит ли кошачьего корма на 4 дня.
   Решение:
   Пусть общий корм \(S\). Потребление в день: \[ \frac{S}{9} + \frac{S}{7} = S\left(\frac{1}{9} + \frac{1}{7}\right) = \frac{16S}{63} \] Время, на которое хватит корма: \[ \frac{S}{\frac{16S}{63}} = \frac{63}{16} \approx 3,9375\,\text{дней} < 4\,\text{дней} \] Ответ: Нет, не хватит.
   
   
5. Вычислите: \(\frac{\left(97\tfrac{4}{15} - 95\tfrac{5}{18}\right)\,\cdot\,2\tfrac{1}{4} + 0,373}{0,3} \;:\;\frac{2}{3}\)
   Решение:
   Последовательно выполним преобразования: \[ 97\frac{4}{15} - 95\frac{5}{18} = \frac{179}{90},\quad \frac{179}{90} \cdot \frac{9}{4} = \frac{179}{40},\quad \frac{179}{40} + 0,373 = 4,848 \] \[ \frac{4,848}{0,3} \cdot \frac{3}{2} = 24,24 \] Ответ: \(24,24\).
   
   
6. Докажите перпендикулярность диагоналей четырёхугольника \(ABCD\) (\(AB = BC\), \(AD = CD\)).
   Решение:
   Точки \(B\) и \(D\) лежат на серединном перпендикуляре отрезка \(AC\) (так как \(AB = BC\) и \(AD = CD\)). Следовательно, \(BD \perp AC\).
   
   
7. На сколько процентов грибов больше собрал Сыроежкин, чем Лисичкин?
   Решение:
   \[ S = 0,35 \cdot 8 = 2,8\,\text{кг},\quad O = \frac{2,8}{0,875} = 3,2\,\text{кг},\quad L = 8 - 2,8 - 3,2 = 2\,\text{кг} \] \[ \frac{2,8 - 2}{2} \cdot 100% = 40\% \] Ответ: \(40\%\).
   
   
8. Сколько весили булочки седьмой няни?
   Решение:
   Система уравнений: \[ \begin{cases} 2m + 3c = 600\\ 4m + o = 350\\ 3c + 5o = 700 \end{cases} \implies m = 75\,\text{г}, \; c = 150\,\text{г}, \; o = 50\,\text{г} \] Каждая няня взяла \(1\,m\), \(1\,c\), \(1\,o\): \[ 75 + 150 + 50 = 275\,\text{г} \] Ответ: \(275\) г.
   
   
9. Разберите геометрическую задачу:
   1. Ответ: \(50^\circ\).
   2. Ответ: \(140^\circ\).
   3. Так как \(BH = CH\), треугольник \(BCH\) равнобедренный.
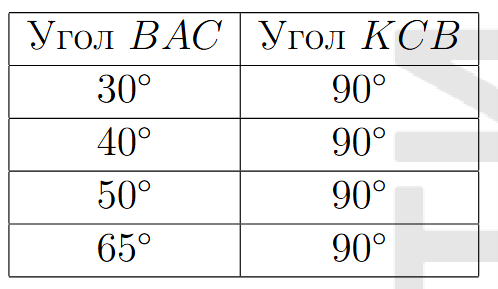
   4. Заполните таблицу:
      
      Закономерность: \(\angle KCB = 90^\circ\) при любом \(\angle BAC\).