Школа Летово из 7 в 8 класс 2022 год вариант 1

1. Вычислите: \[ \frac{5^{10}\cdot(-3)^9}{(-15)^8}. \]
2. Сравните значения выражений: \[ \Bigl(\frac{2}{5}+\frac{3}{4}\Bigr):0,1 \quad\text{и}\quad (4,8-1,2)\cdot\frac{1}{3}. \]
3. В прямоугольном треугольнике \(ABC\) (\(\angle C=90^\circ\)) найдите острый угол между перпендикуляром, опущенным к гипотенузе, и биссектрисой угла \(A\), если угол \(B\) равен \(46^\circ\).
4. 1. Упростите выражение \[ (x-1)(2x+2)(x-3) - 2x^2(x-3). \]
   2. Найдите при каком значении \(x\) справедливо равенство \[ (x-1)(2x+2)(x-3) - 2x^2(x-3) = x - 3. \]
5. Произведение двух чисел равно 50. Первое число увеличили на $30\%$, а второе уменьшили на $20\%$. Чему равно произведение новых чисел?
6. Цветочный город и городок Змеёвка соединены прямой дорогой. На дороге стоят Винтик и Шуршипчик, между ними 1 км. Винтик ближе в Цветочному городу. Если Винтик идёт пешком, то его скорость 4 км/ч, если едет на велосипеде, то его скорость – 24 км/ч. Шуршипчик же бегает со скоростью 12 км/ч. Если коротышки сейчас направятся в Цветочный город, то Винтик пешком доберётся туда одновременно с бегущим Шуршипчиком. Если же они направятся в Змеёвку, то Винтик на велосипеде доберётся туда одновременно с бегущим Шуршипчиком. Каково расстояние между Змеёвкой и Цветочным городом?
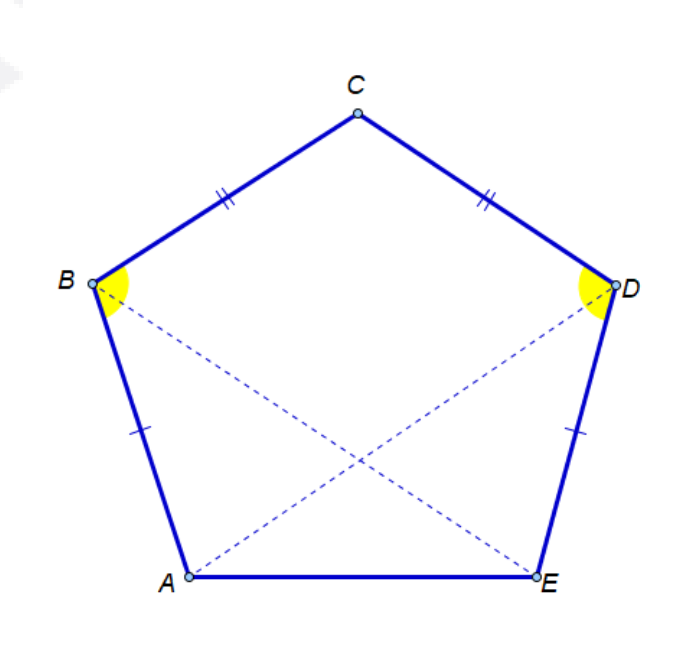
7. Дан пятиугольник \(ABCDE\), в нём \(AB = DE\), \(BC = CD\), \(\angle ABC = \angle CDE\). Докажите, что \(AD\) равно \(BE\).
   
8. Первое число в некоторой последовательности чисел – единица, каждое следующее получается по правилу: к предыдущему числу прибавляется 1 и результат заменяется на обратное число. Например, второе число считается таким образом: \(1 + 1 = 2\), заменяем 2 на обратное и получаем \(\tfrac12\) и т.д. Первые три числа данной последовательности такие: \(1; \tfrac12; \tfrac23\).
   1. Найдите следующие четыре числа данной последовательности.
   2. Какие закономерности вы замечаете в числителях и знаменателях таких чисел?
   3. Могут ли и числитель, и знаменатель полученных чисел быть чётными?
   4. Может ли какое-нибудь такое число быть больше единицы?
   5. Может ли какое-то из чисел последовательности оказаться сокращимой дробью?

Решения задач

1. Вычислите: \[ \frac{5^{10}\cdot(-3)^9}{(-15)^8}. \] Решение: Приведём выражение к общему основанию: \[ \frac{5^{10} \cdot (-3)^9}{(-15)^8} = \frac{5^{10} \cdot (-3)^9}{(-3 \cdot 5)^8} = \frac{5^{10} \cdot (-3)^9}{(-3)^8 \cdot 5^8} = (-3)^{9-8} \cdot 5^{10-8} = (-3) \cdot 5^2 = -75. \] Ответ: \(-75\).
   
   
2. Сравните значения выражений: \[ \Bigl(\frac{2}{5}+\frac{3}{4}\Bigr):0,1 \quad\text{и}\quad (4,8-1,2)\cdot\frac{1}{3}. \] Решение: \[ \Bigl(\frac{8}{20} + \frac{15}{20}\Bigr):0,1 = \frac{23}{20} \cdot 10 = \frac{23}{2} = 11,5. \] \[ (3,6 \cdot \frac{1}{3}) = 1,2. \] Сравниваем \(11,5 > 1,2\).
   Ответ: \((\frac{2}{5} + \frac{3}{4}): 0,1 > (4,8 - 1,2) \cdot \frac{1}{3}\).
   
   
3. В прямоугольном треугольнике \(ABC\) (\(\angle C=90^\circ\)) угол \(B = 46^\circ\). Найдём острый угол между перпендикуляром к гипотенузе и биссектрисой угла \(A\).
   Решение: \(\angle A = 90^\circ - 46^\circ = 44^\circ\). Биссектриса делит угол \(A\) на \(22^\circ\). Пусть \(CH\) — высота, тогда \(\angle HAC = 180^\circ - 90^\circ - 44^\circ = 46^\circ\). Рассмотрим угол между \(CH\) и биссектрисой: \(46^\circ - 22^\circ = 24^\circ\).
   Ответ: \(24^\circ\).
   
   
4. 1. Упростите выражение: \[ (x-1)(2x+2)(x-3) - 2x^2(x-3). \] Решение: Вынесем общий множитель \((x-3)\): \[ (x-3) \cdot \bigl[(x-1)(2x+2) - 2x^2\bigr] = (x-3) \cdot \left[2x^2 - 2 - 2x^2\right] = -2(x-3). \] Ответ: \(-2(x-3)\).
      
      
   2. Найдите \(x\): \[ -2(x - 3) = x - 3. \] Решение: \[ -2x + 6 = x - 3 \quad \Rightarrow \quad -3x = -9 \quad \Rightarrow \quad x = 3. \] Проверка подстановкой подтверждает решение.
      Ответ: \(3\).
   
   
   
5. Произведение двух чисел равно 50. После увеличения первого на $30\%$ и уменьшения второго на $20\%$, новое произведение:
   Решение: Пусть числа \(a\) и \(b\), тогда \(a \cdot b = 50\). Новое произведение: \[ 1,3a \cdot 0,8b = 1,04ab = 1,04 \cdot 50 = 52. \] Ответ: \(52\).
   
   
6. Расстояние между Цветочным городом и Змеёвкой обозначим \(S\). При движении в Цветочный город: \[ \frac{d}{4} = \frac{d + 1}{12} \quad \Rightarrow d = 0,5 \text{ км}. \] При движении в Змеёвку: \[ \frac{S - 0,5}{24} = \frac{S - 1,5}{12} \quad \Rightarrow S - 0,5 = 2(S - 1,5) \quad \Rightarrow S = 2,5. \] Ответ: \(2,5\) км.
   
   
7. Для пятиугольника \(ABCDE\) с условиями \(AB=DE\), \(BC=CD\), \(\angle ABC = \angle CDE\). Построив симметрию относительно середины \(BD\), получим \(AB = DE\), \(BC = CD\), углы равны. Из равенства треугольников \(ABC\) и \(CDE\) сторон \(AD\) и \(BE\) равны.
   Ответ: доказано.
   
   
8. Последовательность: \(1; \frac{1}{2}; \frac{2}{3}; \frac{3}{5}; \frac{5}{8}; \frac{8}{13}; \frac{13}{21}\).
   1. Следующие четыре числа: \(\frac{3}{5}; \frac{5}{8}; \frac{8}{13}; \frac{13}{21}\).
   2. Числитель/знаменатель образуют последовательность Фибоначчи.
   3. Нет, числитель и знаменатель взаимно просты.
   4. Нет, каждое последующее число меньше единицы.
   5. Нет, числитель и знаменатель соседние числа Фибоначчи, взаимно просты.