Школа Летово из 6 в 7 класс 2024 год вариант 1

1. Отмечая свой день рождения, Малыш пригласил Карлсона и ещё шестерых друзей в гости. Карлсону, как самому сладкоежке, он отрезал четвертую часть праздничного торта, себе взял пятую часть оставшегося куска, а всё остальное поделил поровну между остальными своими друзьями. Какой процент от торта получил каждый из друзей?
2. Вычислите: \[ \bigl(1\tfrac{1}{4} \cdot 1,12 \;-\; 1,75 : \tfrac{2}{3}\bigr) :\; 2,1 \;\cdot\; 4\tfrac{5}{7}. \]
3. Расстояние между Старосёлово и Новосёлово 610 км. Из Старосёлово вышел скоростной поезд со скоростью 80 км/ч. Через 1,5 часа навстречу ему из Новосёлово вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов после выхода обычного пассажирского поезда эти поезда встретятся?
4. Решите уравнение: \[ 2\,(4x+3)\;-\;3\,(4x-1)\;=\;4\,(x+2,5). \]
5. После того, как на борт корабля подняли 30 человек, потерпевших кораблекрушение, оказалось, что запасов воды хватит на 50 дней, а не на 60, как было раньше. Сколько людей было на корабле сначала?
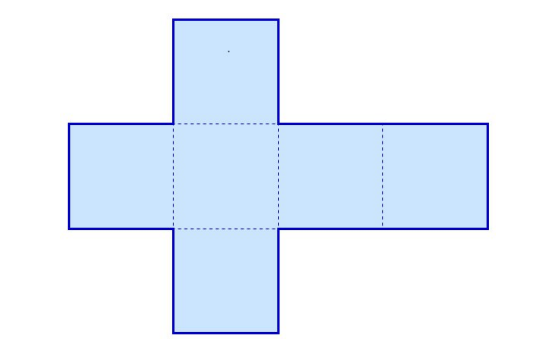
6. На рисунке ниже изображена развёртка кубика. Периметр данной фигуры равен 6 см. Чему равна её площадь?
   
   
   
   
7. Введём новую операцию \(\#\) для двух различных чисел \(a\) и \(b\) следующим образом: \[ a\# b \;=\;(a+b)\!:\!(a-b). \]
   1. Найдите значение \(5\#8\).
   2. Найдите значение \(b\), если \(17\#b=2,4\).
   3. Вычислив значения \(1\#5\) и \(5\#1\), а потом \(3\#4\) и \(4\#3\), Петя решил, что \(a\#b=b\#a\) для любых натуральных чис \(a\) и \(b\). Прав ли Петя? Если Петя прав, то обоснуйте свой ответ. Если Петя неправ, то приведите контрпример (т.е. пример, опровергающий утверждение Пети).
   4. Приведите пример двух непоследовательных натуральных чис \(a\) и \(b\), чтобы \(a\#b\) было целым числом.

Решения задач

1. Отмечая свой день рождения, Малыш пригласил Карлсона и ещё шестерых друзей в гости. Карлсону, как самому сладкоежке, он отрезал четвертую часть праздничного торта, себе взял пятую часть оставшегося куска, а всё остальное поделил поровну между остальными своими друзьями. Какой процент от торта получил каждый из друзей? Решение: Весь торт составляет $100\%$. Карлсон получил $\frac{1}{4}$, что равно $25\%$. Осталось $75\%$. Малыш взял $\frac{1}{5}$ от остатка: $\frac{1}{5} \cdot 75% = 15\%$. Осталось $75% - 15% = 60%$. Это поделили поровну между шестью друзьями: $\frac{60\%}{6} = 10\%$. Ответ: $10\%$.
2. Вычислите: \[ \bigl(1\tfrac{1}{4} \cdot 1,12 \;-\; 1,75 : \tfrac{2}{3}\bigr) :\; 2,1 \;\cdot\; 4\tfrac{5}{7}. \] Решение: Переведём смешанные дроби в неправильные: $1\tfrac{1}{4} = \frac{5}{4}$, $\:4\tfrac{5}{7} = \frac{33}{7}$. Вычислим каждую часть по порядку: \[ \frac{5}{4} \cdot 1,12 = \frac{5}{4} \cdot \frac{28}{25} = 1,4; \] \[ 1,75 : \frac{2}{3} = \frac{7}{4} \cdot \frac{3}{2} = \frac{21}{8} = 2,625; \] Разность: \[ 1,4 - 2,625 = -1,225; \] Деление на $2,1$: \[ -1,225 : 2,1 = -\frac{49}{40} : \frac{21}{10} = -\frac{7}{12}; \] Умножение на $\frac{33}{7}$: \[ -\frac{7}{12} \cdot \frac{33}{7} = -\frac{33}{12} = -2,75. \] Ответ: $-2,75$.
3. Расстояние между Старосёлово и Новосёлово 610 км. Из Старосёлово вышел скоростной поезд со скоростью 80 км/ч. Через 1,5 часа навстречу ему из Новосёлово вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов после выхода обычного пассажирского поезда эти поезда встретятся? Решение: За 1,5 часа скоростной поезд проехал: \[ 80 \cdot 1,5 = 120 \text{ (км)}. \] Оставшееся расстояние между поездами: \[ 610 - 120 = 490 \text{ (км)}. \] Скорость сближения: \[ 80 + 60 = 140 \text{ км/ч}. \] Время до встречи: \[ \frac{490}{140} = 3,5 \text{ часов}. \] Ответ: через 3,5 часа.
4. Решите уравнение: \[ 2\,(4x+3)\;-\;3\,(4x-1)\;=\;4\,(x+2,5). \] Решение: Раскроем скобки: \[ 8x + 6 - 12x + 3 = 4x + 10; \] Упростим уравнение: \[ -4x + 9 = 4x + 10; \] Переносим слагаемые: \[ -8x = 1 \quad \Rightarrow \quad x = -\frac{1}{8} = -0,125. \] Ответ: $-\dfrac{1}{8}$ (или $-0,125$).
5. После того, как на борт корабля подняли 30 человек, потерпевших кораблекрушение, оказалось, что запасов воды хватит на 50 дней, а не на 60, как было раньше. Сколько людей было на корабле сначала? Решение: Объём воды постоянен. Пусть первоначально было $x$ человек: \[ 60 \cdot x = 50 \cdot (x + 30); \] Решаем уравнение: \[ 60x = 50x + 1500 \quad \Rightarrow \quad 10x = 1500 \quad \Rightarrow \quad x = 150. \] Ответ: 150 человек.
6. На рисунке ниже изображена развёртка кубика. Периметр данной фигуры равен 6 см. Чему равна её площадь? Решение: Стандартная развёртка кубика состоит из шести квадратов в форме креста с периметром 12 сторон квадрата. Из условия периметр равен 6 см: \[ 12a = 6 \quad \Rightarrow \quad a = 0,5 \text{ см}. \] Площадь одного квадрата: \[ 0,5^2 = 0,25 \text{ см}^2. \] Общая площадь развёртки (4 квадрата в кресте и два дополнительных): \[ 6 \cdot 0,25 = 1,5 \text{ см}^2. \] Ответ: $1,5$ см².
7. Введём новую операцию \(\#\) для двух различных чисел \(a\) и \(b\) следующим образом: \[ a\# b \;=\;(a+b)\!:\!(a-b). \]
   1. Найдите значение \(5\#8\). Решение: \[ 5\#8 = \frac{5+8}{5-8} = \frac{13}{-3} = -\frac{13}{3}. \] Ответ: $-4\tfrac{1}{3}$.
   2. Найдите значение \(b\), если \(17\#b=2,4\). Решение: \[ \frac{17 + b}{17 - b} = 2,4; \] \[ 17 + b = 2,4(17 - b); \] \[ 17 + b = 40,8 - 2,4b; \] \[ 3,4b = 23,8 \quad \Rightarrow \quad b = \frac{23,8}{3,4} = 7. \] Ответ: 7.
   3. Выяснить, верно ли \(a\#b = b\#a\). Решение: Контрпример — числа 1 и 5: \[ 1\#5 = \frac{1+5}{1-5} = -1,5; \quad 5\#1 = \frac{5+1}{5-1} = 1,5. \] Ответ: неверно.
   4. Пример чисел с целым результатом. Решение: Например, $4\#2$: \[ \frac{4 + 2}{4 - 2} = \frac{6}{2} = 3. \] Ответ: 4 и 2.