Школа Летово из 6 в 7 класс 2022 год вариант 1

1. На соревнованиях по бегу через каждые 300 м от места старта стоит наблюдатель, а через каждые 800 м от места старта можно попить воды. На каком расстоянии от места старта можно в первый раз попить воды рядом с наблюдателем? Объясните ваш ответ.
2. Вычислите \[ 4 - \bigl(4 \tfrac{3}{4} - 3,25\bigr) : 1\tfrac{1}{20}. \]
3. 8 одинаковых яблок и 11 одинаковых груш весят столько же, сколько 16 таких же яблок и 6 таких же груш. Что легче: яблоко или груша? Ответ объясните.
4. Расстояние между Москвой и Петербургом по железной дороге 650 км. Из Москвы выехал пассажирский поезд со скоростью 75 км/ч. А через 40 минут из Петербурга в Москву вышел скорый поезд со скоростью 165 км/ч. Через какое время от начала движения поезда из Москвы оба поезда встретятся?
5. Найдите неизвестное \[ \frac{x+1}{0,8} = \frac{13}{1,2}. \]
6. 1. Разрежьте квадрат \(4\times4\) клетки по линиям клеток на две равные фигуры с периметром 14 (сторона клетки равна 1).
      
      
      
      
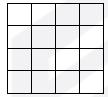
   2. Разрежьте квадрат \(4\times4\) клетки по линиям клеток на две фигуры равной площади, у которых один периметр больше другого на 6.
      
      
      
      
7. Первое число в некоторой последовательности чисел – единица, каждое следующее получается по правилу: к предыдущему числу прибавляется 1 и результат заменяется на обратное число. Например, второе число считается таким образом: \(1 + 1 = 2\), заменяем \(2\) на обратное и получаем \(\tfrac12\) и т. д. Первые три числа данной последовательности такие: \(1\), \(\tfrac12\), \(\tfrac23\).
   1. Найдите следующие четыре числа данной последовательности.
   2. Какие закономерности вы замечаете в числителях и знаменателях таких чисел?
   3. Могут ли и числитель, и знаменатель полученных чисел быть чётными?
   4. Может ли какое-нибудь такое число быть больше единицы?
   5. Может ли какое-то из чисел последовательности оказаться сократимой дробью?

Решения задач

1. Найти первое общее кратное чисел 300 и 800. Разложим их на множители:
   $300 = 2^2 \cdot 3 \cdot 5^2$
   $800 = 2^5 \cdot 5^2$
   НОК$(300;800) = 2^5 \cdot 3 \cdot 5^2 = 2400$ м = 2,4 км.
   Ответ: 2400 м.
2. Вычисление:
   $4 - \bigl(4\tfrac{3}{4} - 3,25\bigr) : 1\tfrac{1}{20}$
   Приведём дроби:
   $4\tfrac{3}{4} = \frac{19}{4}$, $3,25 = \frac{13}{4}$, $1\tfrac{1}{20} = \frac{21}{20}$
   Выполняем вычитание в скобках:
   $\frac{19}{4} - \frac{13}{4} = \frac{6}{4} = \frac{3}{2}$
   Деление: $\frac{3}{2} : \frac{21}{20} = \frac{3}{2} \cdot \frac{20}{21} = \frac{60}{42} = \frac{10}{7}$
   Итог: $4 - \frac{10}{7} = \frac{28}{7} - \frac{10}{7} = \frac{18}{7} = 2\tfrac{4}{7}$
   Ответ: $2\tfrac{4}{7}$.
3. Сравним массы:
   $8я + 11г = 16я + 6г$
   Вычтем $8я + 6г$ с обеих сторон:
   $5г = 8я$ → $1г = \frac{8}{5}я$
   Вес груши больше веса яблока. Значит, яблоко легче.
   Ответ: яблоко.
4. Пусть до встречи поезд из Москвы ехал $t$ часов, тогда скорый $\left(t - \frac{2}{3}\right)$ часов. Составляем уравнение:
   $75t + 165\left(t - \frac{2}{3}\right) = 650$
   $75t + 165t - 110 = 650$
   $240t = 760$ → $t = \frac{760}{240} = 3\frac{1}{6}$ ч = 3 ч 10 мин.
   Ответ: 3 ч 10 мин.
5. Решаем пропорцию:
   $\frac{x+1}{0,8} = \frac{13}{1,2}$
   Перемножаем крест-накрест:
   $(x+1) \cdot 1,2 = 13 \cdot 0,8$
   $1,2x + 1,2 = 10,4$
   $1,2x = 9,2$ → $x = \frac{9,2}{1,2} = \frac{23}{3} = 7\frac{2}{3}$
   Ответ: $7\tfrac{2}{3}$.
6. 1. Пример разреза:
      
      Разрезать квадрат горизонтальной ступенчатой линией так, чтобы каждая половина имела по 14 единиц периметра.
   2. Пример разреза:
      
      Вырезать прямоугольник 2×4 из одного угла. Одна часть будет иметь периметр 18 (длинная L-образная), другая 12 (прямоугольник 2×4).
      Разница: $18 - 12 = 6$.
7. 1. Следующие четыре числа:
      4: $\frac{2}{3} + 1 = \frac{5}{3}$ → $\frac{3}{5}$;
      5: $\frac{3}{5} + 1 = \frac{8}{5}$ → $\frac{5}{8}$;
      6: $\frac{5}{8} + 1 = \frac{13}{8}$ → $\frac{8}{13}$;
      7: $\frac{8}{13} + 1 = \frac{21}{13}$ → $\frac{13}{21}$.
      Ответ: $\tfrac{3}{5}, \tfrac{5}{8}, \tfrac{8}{13}, \tfrac{13}{21}$.
   2. Числители и знаменатели последовательности образуют последовательность Фибоначчи: числители 1,2,3,5,8,13,…, знаменатели 1,1,2,3,5,8,…
   3. Нет. Последовательные числа Фибоначчи взаимно просты и не могут быть оба чётными.
   4. Нет. Каждый последующий элемент — обратное число к величине больше 1, значит дробь меньше 1.
   5. Нет. Дроби Фибоначчи несократимы, так как соседние числа Фибоначчи взаимно просты.