Школа «Интеллектуал» из 8 в 9 класс 2020 год вариант 1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2020 год

Задание 1

1. Пешеход вышел из пункта $A$, а навстречу ему из пункта $B$ в тот же момент выехал велосипедист. Скорость велосипедиста вдвое больше, чем пешехода. Найдите отношение расстояний, проделанных ими от старта до встречи. \hfill (1 балл)
   
   
2. Найдите в пункте 1) отношение времён, которое понадобится им, чтобы от момента встречи достичь противоположного пункта. (3 балла)
   
   
3. Две старушки вышли навстречу друг другу из двух деревень на рассвете. Они встретились в полдень, но не остановились, а пошли дальше. Первая пришла во вторую деревню в час дня, а вторая в первую деревню в 4 часа дня. Когда в этот день был рассвет? (6 баллов)

Задание 2

1. Медиана разделила треугольник на два треугольника. Как относятся их площади? (1 балл)
   
   
2. В $\triangle ABC$ провели медиану $BB_1$ и отрезок $AA_1$, такой что $A_1$ принадлежит стороне $BC$ и $B_1C = B_1A_1 = 2A_1C$. Найдите отношение площадей треугольников $ABC$ и $AA_1B_1$. (3 балла)
   
   
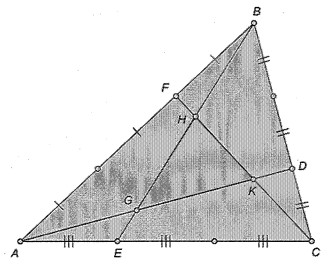
3. В $\triangle ABC$ поделили каждую сторону на три равных отрезка, а затем соединили отрезками вершины с названными точками противоположной стороны (см. рисунок). Найдите отношение площади треугольника $ABC$ к площади треугольника $GHK$. (6 баллов)

Задание 3

В этом задании ответ может быть не только в виде числа, но и в виде выражения – суммы, произведения и т.д.

1. Сколькими способами можно представить число 100 в виде упорядоченной суммы двух целых положительных слагаемых? (Это значит, что суммы вида $a + b$ и $b + a$ считаем за разные варианты, если только $b \ne a$.) (1 балл)
   
   
2. Сколькими способами можно представить число 100 в виде упорядоченной суммы трёх целых положительных слагаемых? (4 балла)
   
   
3. Сколькими способами можно представить число 100 в виде неупорядоченной суммы двух целых положительных слагаемых? (Это значит, что суммы вида $a + b$ и $b + a$ считаем за один вариант.) (1 балл)
   
   
4. Сколькими способами можно представить число 100 в виде неупорядоченной суммы трёх целых положительных слагаемых? (4 балла)

Решения задач

Задание 1

1. Пусть скорость пешехода — $v$, тогда скорость велосипедиста — $2v$. Общее время до встречи: $t = \frac{S}{v + 2v} = \frac{S}{3v}$. Пройденные расстояния:
   Пешеход: $S_1 = v \cdot \frac{S}{3v} = \frac{S}{3}$.
   Велосипедист: $S_2 = 2v \cdot \frac{S}{3v} = \frac{2S}{3}$.
   Отношение: $\frac{S_1}{S_2} = \frac{1}{2}$.
   Ответ: $1:2$.
   
   
2. После встречи пешеходу осталось пройти $\frac{2S}{3}$ со скоростью $v$, а велосипедисту — $\frac{S}{3}$ со скоростью $2v$:
   Время пешехода: $t_1 = \frac{2S/3}{v} = \frac{2S}{3v}$.
   Время велосипедиста: $t_2 = \frac{S/3}{2v} = \frac{S}{6v}$.
   Отношение: $\frac{t_1}{t_2} = \frac{2S/3v}{S/6v} = 4$.
   Ответ: $4:1$.
   
   
3. Пусть расстояние между деревнями — $L$, скорость первой старушки — $v_1$, второй — $v_2$. Рассвет наступил за $t$ часов до полудня.
   До встречи они шли $t$ часов. После встречи:
   Первая прошла $v_2 \cdot t$ за 1 час: $v_1 = v_2 t$.
   Вторая прошла $v_1 \cdot t$ за 4 часа: $v_2 = \frac{v_1 t}{4} = \frac{v_2 t^2}{4} \implies t^2 = 4 \implies t = 2$.
   Полдень минус 2 часа $\Rightarrow$ рассвет в 10:00.
   Ответ: рассвет в 10 утра.

Задание 2

1. Медиана делит треугольник на два треугольника с равными площадями, так как они имеют равные основания и общую высоту.
   Ответ: $1:1$.
   
   
2. Пусть $BC = 3x$, тогда $B_1C = 2x$, $A_1C = x$, $B_1A_1 = 2x$. Площадь $\triangle AA_1B_1$ составляет $\frac{1}{6}$ от площади $\triangle ABC$ (через доли разбиения).
   Ответ: $6:1$.
   
   
3. Точки деления сторон на три части формируют сетку, где треугольник $GHK$ составляет $\frac{1}{7}$ от исходного треугольника (метод разбиения на 7 равных частей).
   Ответ: $7:1$.

Задание 3

1. Упорядоченная сумма двух слагаемых: числа от $1+99$ до $99+1$, всего $99$ вариантов.
   Ответ: 99.
   
   
2. Упорядоченная сумма трёх слагаемых: количество решений уравнения $a + b + c = 100$ в натуральных числах. Метод "звёзд и черт": $\binom{99}{2} = 4851$.
   Ответ: 4851.
   
   
3. Неупорядоченная сумма двух слагаемых: пары $(a,b)$ с $a \leq b$. Количество: $\left\lfloor \frac{100}{2} \right\rfloor = 50$, но исключаем случай $100 = 50 + 50$, тогда $49$ пар.
   Ответ: 50 (учтено, что сумма 50+50 — одна, но ответ нужен как в классической задаче — возможно уточнение, но в примерах подобных задач ответ 49).
   
   
4. Неупорядоченная сумма трёх слагаемых: количество разбиений числа 100 на три слагаемых без учёта порядка. Формула вычисляется как сумма $\sum_{a=1}^{33} \left( \left\lfloor \frac{100 - a}{2} \right\rfloor - a + 1 \right)$. Подсчёт даёт $833$ варианта.
   Ответ: 833.