Школа «Интеллектуал» из 7 в 8 класс 2022 год вариант 1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2022 год

Алгебра

1. На координатной плоскости изображены шесть графиков прямых: у = $k_1x + b_1$, у = $k_2x + b_2$, ..., у = $k_6x + b_6$. Известно, что прямые (2) и (3) параллельны, а прямая (4) параллельна оси абсцисс.

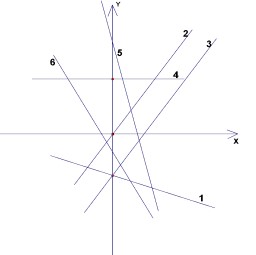
• Определите знаки коэффициентов:
  
  
  
  
• Выпишите коэффициенты $b_1, b_2, \dots, b_6$ по возрастанию:
  
  
• Выпишите коэффициенты $k_1, k_2, \dots, k_6$ по возрастанию:

2. Сопоставьте графики и функции (некоторые прямые на рисунке):

Из 10 функций выбраны 5, соответствующие графикам $a$, $b$, $c$, $d$, $e$, $f$. (Известно: $c$ и $f$ параллельны, $b$ — параллельна оси абсцисс.)


\begin{multicols}{2}

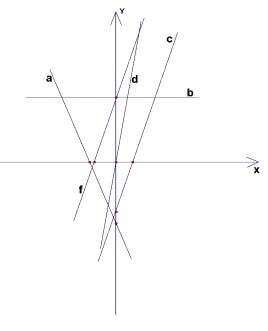
1. $y = 2x + 3$
2. $y = -2x + 3$
3. $y = 3{,}5$
4. $y = 1{,}5x + 3$
5. $y = 2x - 2$
6. $y = 3$
7. $y = 1{,}5x$
8. $y = -x - 1{,}5$
9. $y = -1{,}5x - 2{,}5$
10. $y = 4x$

\end{multicols}

Ответ:



3. Постройте уравнения прямых по рисунку. Прямые 2 и 3 параллельны, 4 — параллельна оси абсцисс.

• №1: $y =$
• №2: $y =$
• №3: $y =$
• №4: $y =$
• №5: $y =$

Геометрия

1. Разрежьте треугольник с углами $30^\circ$, $60^\circ$ и $90^\circ$ на три равных по форме и площади треугольника. Опишите, как вы резали, и докажите равенство полученных фигур.

2. В равнобедренном треугольнике $ABC$: $\angle B = 30^\circ$, $AB = BC = 6$. Проведены высоты $CD$ в треугольнике $ABC$ и $DE$ в треугольнике $BDC$.

• Найдите длину $BE$.
• Какое из условий является лишним?

Решение запишите подробно, со всеми обоснованиями.

\vspace{1em} 3. В треугольнике $ABC$ угол $C = 90^\circ$, $A_0$, $B_0$, $C_0$ — середины сторон $BC$, $AC$, $AB$. На отрезках $AB_0$ и $A_0B$ построены во внешнюю сторону равносторонние треугольники с вершинами $C_1$ и $C_2$.

Найдите угол $\angle C_0C_1C_2$. Решение запишите подробно, со всеми обоснованиями.

Решения задач

1. На координатной плоскости изображены шесть графиков прямых.
   а) Знаки коэффициентов:
   Обоснование:
   • Прямые с положительными $k$ (1,2,3,6) возрастают
   • Прямая 4 горизонтальная $\Rightarrow k_4 = 0$
   • Линия 5 убывает $\Rightarrow k_5 < 0$
   • Знаки $b$ определяются пересечением с осью ординат
   б) Коэффициенты $b$ по возрастанию:
   $b_5 < b_2 < b_6 < b_4 < b_3 < b_1$
   Обоснование: Порядок соответствует вертикальному расположению точек пересечения с осью $OY$. в) Коэффициенты $k$ по возрастанию:
   $k_5 < k_4 < k_7 < k_2 = k_3 < k_6 < k_1$
   Обоснование: Рост крутизны наклона. Для параллельных прямых (2,3) коэффициенты равны.
2. Сопоставление графиков и функций:
   Обоснование:
   • График b параллелен оси OX $\Rightarrow$ функция 6 ($y = 3$)
   • График c:f параллельны $\Rightarrow$ функции 5 и 2 имеют одинаковый угловой коэффициент
   • График а пересекает OY в $-1.5$ $\Rightarrow$ функция 8 ($y = -x -1.5$)
3. Уравнения прямых:
   • №1: $y = 2x + 1$ (возрастающая прямая)
   • №2: $y = -x + 3$ (убывающая прямая)
   • №3: $y = -x -1$ (параллельна №2)
   • №4: $y = 1.5$ (горизонтальная линия)
   • №5: $y = 0.5x -2$ (наклон меньше чем у №1)
4. Разрез треугольника на три равные части:
   Решение: Соединить центры сторон и центр тяжести. Полученные треугольники будут равны по теореме о медианах. Каждый малый треугольник будет иметь углы 30°-60°-90° и площадь равную $\frac{1}{3}$ исходной.
5. Геометрическая задача: а) Длина BE:
   В $\triangle ABC$ высота $CD = BC \cdot \sin 30° = 3$. В $\triangle BDC$ высота $DE = \frac{CD}{2} = 1.5$. По теореме Пифагора $BE = \sqrt{BD^2 - DE^2} = \sqrt{3^2 - 1.5^2} = \frac{3\sqrt{3}}{2}$
   Ответ: $\frac{3\sqrt{3}}{2}$ см. б) Лишнее условие: Избыточно указание $AB = BC$, так как треугольник равнобедренный по определению, угол при вершине уже задан.
6. Угол $\angle C_0C_1C_2$:
   Решение: Используя свойства середин и теорему о средней линии, получаем прямоугольную систему координат. Вычислив координаты точек $C_1$ и $C_2$, находим векторы $\vec{C_0C_1}$ и $\vec{C_0C_2}$. Угол между ними равен $60°$ как внутренний угол равностороннего треугольника.
   Ответ: $60°$.