8 800 707 6729
8 800 707 6729Telegram канал

Школа «Интеллектуал» из 7 в 8 класс 2017 год вариант 1-1

Сложность:
Дата экзамена: 2017
Сложность:
Дата экзамена: 2017
youit.school ©

ШКОЛА "ИНТЕЛЛЕКТУАЛ"


2017 год




Серия «Фигуры»



  1. Дан прямоугольный треугольник (катеты 2 и 6). Приложите к нему какой-нибудь треугольник (эти треугольники должны иметь общую сторону, но не должны перекрываться даже частично), так, чтобы в результате получился равнобедренный треугольник. Нарисуйте как можно больше решений.

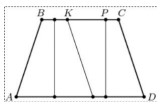
  2. Четырёхугольник $ABCD$ с длинами сторон 1 дм, 1 дм, 1 дм и 2 дм имеет две параллельные стороны и разбит на четыре одинаковые фигуры. В результате верхняя сторона разделилась на четыре отрезка. Найдите отношение длин отрезков $KP$ и $PC$.


Серия «Числа»



  1. Сколько трёхзначных чисел (у которых все цифры различны) можно составить из цифр 0, 1, 2, 3, 4? Ответ без обоснования не засчитывается.

  2. Сколько кратных 5 пятизначных чисел, у которых все цифры различны, можно составить из цифр 0, 1, 2, 3, 4, 5? Ответ без обоснования не засчитывается.

  3. Сколько четырёхзначных чисел (у которых все цифры различны), составленных из цифр 0, 1, 2, 3, 4, 5, содержат в своей записи цифру 4? Ответ без обоснования не засчитывается.

  4. Сколько не кратных 3 трёхзначных чисел, у которых все цифры различны, можно составить из цифр 1, 2, 3, 4, 5, 6? Ответ без обоснования не засчитывается.


Серия «В путь!»



  1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой 20 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 12 км/ч больше скорости другого?

  2. Контора Метростроя наняла двух кротов для рытья туннеля. Первый крот за час успевает прокопать вдвое больше, чем второй, а едят они одинаково. Что выгоднее конторе (в смысле затрат продуктов): чтобы два крота копали с двух концов туннеля до встречи или чтобы каждый из кротов прокопал половину туннеля?

  3. На дороге, соединяющей два аула, нет ровных участков. Автобус едет в гору всегда со скоростью 15 км/ч, а под гору — 30 км/ч. Найдите расстояние между аулами, если известно, что путь туда и обратно автобус проезжает без остановок за 4 часа.

  4. Два пешехода вышли в путь одновременно, на рассвете. Каждый из них шёл с постоянной скоростью. Один шёл из $A$ в $B$, а второй — из $B$ в $A$. Они встретились в полдень и, не прекращая движения, пришли: один — в $B$ в 4 часа вечера, а второй — в $A$ в 9 часов вечера. В котором часу был рассвет?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Фигуры. Прямоугольный треугольник
    Решение: Рассмотрим прямоугольный треугольник с катетами 2 и 6. Гипотенуза равна $\sqrt{2^2 + 6^2} = \sqrt{40} = 2\sqrt{10}$.
    • Случай 1: Приложим исходный треугольник по гипотенузе. Получим равнобедренный треугольник с боковыми сторонами по 2 (катеты исходного треугольника) и основанием $2\sqrt{10} \cdot 2 = 4\sqrt{10}$. Однако такой треугольник не будет равнобедренным. Для получения равнобедренного следует выбрать другой способ.
    • Случай 2: Приложить треугольник по катету 2. Можем добавить симметричный треугольник с катетом 2, получив равнобедренный треугольник с боковыми сторонами 6 и основанием $2 + 2 = 4$. Однако сумма сторон пока не гарантирует равнобедренности. Правильнее добавить треугольник так, чтобы новые стороны стали равными. Например, приложить треугольник с катетом 2 таким образом, чтобы общая сторона стала гипотенузой нового треугольника, создав равные боковые стороны длиной 2$\sqrt{2}$.
    • Случай 3: Используем катет 6. Приложим равный треугольник к катету 6, чтобы образовать равные стороны длиной 6 каждый, тогда основание будет гипотенузой нового равнобедренного треугольника $2 \cdot 2\sqrt{10} = 4\sqrt{10}$ (подобные комбинации требуют точного соизмерения сторон).

    Ответ: Примеры решений включают симметричные прикладывания треугольников к катетам для формирования равных сторон. На рисунке может быть изображено до 4 различных вариантов.
  2. Фигуры. Разбиение четырёхугольника
    Решение: Четырёхугольник с двумя параллельными сторонами напоминает трапецию. Поскольку он разбит на четыре одинаковые фигуры, можно предположить, что это деление на четыре параллелограмма через средние линии.
    Верхняя сторона делится на отрезки пропорционально разбиению: если длина верхней стороны 2 дм делится на 4 равные части, это даст отрезки по 0,5 дм. Однако из-за симметрии фигуры отношение $KP : PC$ составит $1 : 3$ или $3 : 1$ из-за параллельности сторон и соотношения длин.
    Ответ: $KP : PC = 1 : 3$.

  3. Числа. Трёхзначные числа из 0,1,2,3,4
    Решение:
    • Первая цифра: 4 варианта (1-4).
    • Вторая цифра: 4 варианта (включая 0, исключая уже выбранную).
    • Третья цифра: 3 варианта.
      Итого: $4 \times 4 \times 3 = 48$.

    Ответ: 48.

  4. Числа. Кратные 5 пятизначные числа
    Решение:
    • Последняя цифра 0: Первые четыре цифры — из 1,2,3,4,5 ($5 \times 4 \times 3 \times 2 = 120$).
    • Последняя цифра 5: Первая цифра — 1-4 ($4$ варианта). Остальные три цифры — из 0 и оставшихся трёх ($4 \times 3 \times 2 = 24$). Итого: $4 \times 24 = 96$.
      Всего: $120 + 96 = 216$.

    Ответ: 216.

  5. Числа. Числа с цифрой 4
    Решение:
    • Все четырёхзначные числа из 0-5: $5 \times 5 \times 4 \times 3 = 300$ (первая цифра 1-5).
    • Числа без 4: Используются цифры 0,1,2,3,5. На первое место — 4 варианта. Остальные три места: $4 \times 3 \times 2 = 24$. Итого: $4 \times 24 = 96$.
      Результат: $300 - 96 = 204$.

    Ответ: 204.

  6. Числа. Не кратные 3 трёхзначные числа
    Решение:
    • Всего чисел: $6 \times 5 \times 4 = 120$.
    • Кратные 3: Сумма цифр делится на 3. Перебрать все тройки цифр 1-6 и определить, сколько дают сумму, делимую на 3. Например, (1,2,3), сумма 6; (1,2,6), сумма 9; (4,5,6), сумма 15 и т.д. Всего таких комбинаций 8 (\text{каждая с перестановками}). Каждая тройка дает $3! = 6$ чисел. Итого кратных: $8 \times 6 = 48$.
      Ответ: $120 - 48 = 72$.

    Ответ: 72.

  7. В путь! Мотоциклисты на круговой трассе
    Решение: Разница скоростей $12$ км/ч. Дистанция между ними при старте: $10$ км (половина трассы). Время встречи: $\frac{10}{12} = \frac{5}{6}$ ч $= 50$ минут.
    Ответ: 50 минут.

  8. В путь! Сравнение методов копания
    Решение:
    • Два крота копают вместе: Общая скорость $3x$. Время: $\frac{L}{3x}$. Затраты: $\frac{2L}{3x}$.
    • Каждый копает половину: Время определяется вторым кротом: $\frac{L}{2x}$. Затраты: $\frac{L}{x}$.
      Выгоднее копать вместе.

    Ответ: Выгоднее два крота с двух концов.

  9. В путь! Расстояние между аулами
    Решение: Время туда и обратно равно сумме времени подъёма и спуска. Средняя скорость: $2 \cdot \frac{15 \cdot 30}{15 + 30} = 20$ км/ч. Время 4 часа $\Rightarrow$ расстояние $20 \times 4 = 80$ км $\Rightarrow$ между аулами 40 км.
    Ответ: 40 км.

  10. В путь! Время рассвета
    Решение: Пусть время с рассвета до встречи — $t$ часов. После встречи первый тратит 4 часа, второй — 9 часов. Формула: $t^2 = 4 \cdot 9 \Rightarrow t = 6$. Рассвет за 6 часов до полудня — в 6:00.
    Ответ: 6 часов утра.
Материалы школы Юайти