Школа «Интеллектуал» из 6 в 7 класс 2024 год вариант 1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2024 год

1. [1 балл] Возраст нескольких друзей составляет в сумме 62 года. Через 3 года он будет составлять 80 лет. Сколько этих друзей?
   Требуется только ответ.
   
   
2. [2 балла] Для 112 полок длиной 75 см нужны доски. В магазине есть только четырёхметровые доски. Сколько досок нужно купить?
   Требуется только ответ.
   
   
3. [3 балла] Площадь меньшего прямоугольника на рисунке — 48 см². Найдите площадь большего прямоугольника.
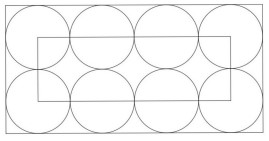   Требуется полное решение.
   
   
4. [3 балла] Прямоугольник 3×5 клеток, в центре — дырка. Найдите 5 разных способов разрезать фигуру на 2 равные части по линиям сетки.
   Требуется только ответ.
   
   
5. [2 балла] На поляне 25 гномов. 1) Каждый, кто надел колпак, был и в обуви; 2) Без колпака пришли 12 гномов; 3) Босиком — 5 гномов. Кого больше — тех, кто в обуви, но без колпака, или тех, кто в колпаке, и на сколько?
   Требуется полное решение.
   
   
6. [3 балла] Сколько пятизначных чисел содержат хотя бы одну цифру 8?
   Требуется только ответ.
   
   
7. [3 балла] Мама и Аня встретились через 30 минут после начала пути. Вернулись домой на 20 минут раньше обычного. Насколько раньше закончились танцы?
   Требуется полное решение.
   
   
8. [3 балла] Мяч брошен с крыши 16 м, отскакивает на ¾ от высоты. Сколько раз пролетит мимо гусеницы на вершине шестиметрового дерева?
   Требуется полное решение.

Решения задач

1. Возраст нескольких друзей составляет в сумме 62 года. Через 3 года он будет составлять 80 лет. Сколько этих друзей?
   Решение: Через 3 года возраст каждого друга увеличится на 3 года.
   Разница между суммарным возрастом через 3 года и текущим:
   $80 - 62 = 18$ лет.
   Количество друзей: $\frac{18}{3} = 6$.
   Ответ: 6.
   
   
2. Для 112 полок длиной 75 см нужны доски. В магазине есть только четырёхметровые доски. Сколько досок нужно купить?
   Решение: Общая необходимая длина досок:
   $112 \cdot 75 = 8400$ см = 84 м.
   Одна доска — 4 м, значит для распила:
   Каждая четырёхметровая доска позволяет получить $\left\lfloor \frac{400}{75} \right\rfloor = 5$ полок с остатком 25 см.
   Требуемое количество досок: $\left\lceil \frac{112}{5} \right\rceil = 23$.
   Ответ: 23.
   
   
3. Площадь меньшего прямоугольника на рисунке — 48 см². Найдите площадь большего прямоугольника.
   Решение: Меньший прямоугольник состоит из 3 равных квадратов площадью $48 \div 3 = 16$ см² каждый (сторона 4 см).
   Больший прямоугольник содержит $8$ таких квадратов:
   $16 \cdot 8 = 128$ см².
   Ответ: 128 см².
   
   
4. Прямоугольник 3×5 клеток, в центре — дырка. Найдите 5 разных способов разрезать фигуру на 2 равные части по линиям сетки.
   Ответ: Пять примеров симметричных разрезов:
   Критерий: 5 различных симметричных разрезов.
   
   
5. На поляне 25 гномов.
   1) В колпаке и обуви — 13 гномов (так как 25-12=13).
   2) Всего обутых — 20 гномов (25-5=20).
   Те, кто в обуви без колпака: $20 - 13 = 7$.
   Разница: $13 - 7 = 6$.
   Ответ: тех, кто в колпаке, больше на 6.
   
   
6. Сколько пятизначных чисел содержат хотя бы одну цифру 8?
   Решение: Всего пятизначных чисел — 90000 (от 10000 до 99999).
   Числ\u{a0}без цифры 8:
   Первая цифра — 8 вариантов (1-9 без 8).
   Остальные цифры — 9 вариантов каждая (0-9 без 8).
   Итого: $8 \cdot 9^4 = 52488$.
   Ответ: $90000 - 52488 = 37512$.
   
   
7. Мама и Аня встретились через 30 минут после начала пути. Вернулись домой на 20 минут раньше обычного. Насколько раньше закончились танцы?
   Решение: Экономия времени в пути составила 20 минут, что соответствует двусторонней экономии:
   На путь до встречи и обратно экономится по 10 минут в каждом направлении.
   Танцы закончились на $20 \cdot 2 = 40$ минут раньше.
   Ответ: на 40 минут раньше.
   
   
8. Мяч брошен с крыши 16 м, отскакивает на $\frac{3}{4}$ от высоты. Сколько раз пролетит мимо гусеницы на вершине шестиметрового дерева?
   Решение: Высоты отскоков:
   16 → 12 → 9 → 6.75 → 5.0625...
   Проходы мимо 6 м:
   1) Спадение с 16 м — пересечение 6 м (1 раз).
   2) Подъем до 12 м и спуск — пересечения при подъёме (2) и спуске (3).
   3) Подъем до 9 м и спуск — пересечения при подъёме (4) и спуске (5).
   4) Подъем до 6.75 м и спуск — пересечения при подъёме (6) и спуске (7).
   Далее высота меньше 6 м. Итого: 7 раз.
   Ответ: 7.