Школа «Интеллектуал» из 6 в 7 класс 2022 год вариант 1-1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2022 год

1. К числу 76 дописали по одной цифре слева и справа. Полученное четырёхзначное число делится на 15. Найдите все такие варианты. Требуется полное решение.
   
   
2. Представьте число 276 в виде суммы трёх слагаемых $a$, $b$, $c$. При этом: \[ a : b = \frac{1}{3}, \quad b : c = \frac{6}{5} \] Требуется полное решение.
   
   
3. Саша заказал пиццу диаметром 30 см, но затем сменил заказ на пиццу диаметром 40 см. Вычислите, на сколько процентов увеличилась площадь пиццы. Ответ запишите в виде обыкновенной смешанной дроби. Требуется аккуратное вычисление.
   
   
4. Разрежьте фигуру (на рисунке) на 4 равные по форме и площади части. Разрезать можно не только по линиям клеток.
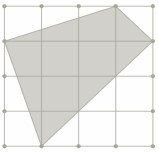   Требуется только ответ.
   
   
5. Решите уравнение: \[ |x + 2{,}5| = 1 \] Требуется аккуратное решение.
   
   
6. За 9 кг яблок заплатили столько же, сколько за $7{,}2$ кг бананов. Сколько стоит 1 кг каждого вида фруктов, если 2 кг бананов дороже 2 кг яблок на 40 рублей? Требуется полное решение.
   
   
7. Охотник со сворой собак едет в город на лошади со скоростью 12 км/ч. Каждые полчаса он отпускает одну собаку — она бежит в город со скоростью 15 км/ч. Сколько времени (в минутах) проходит между прибежавшими подряд собаками? Требуется полное решение.

Решения задач

1. К числу 76 дописали по одной цифре слева и справа. Полученное четырёхзначное число делится на 15. Найдите все такие варианты.
   Решение: Число делится на 15, если делится на 3 и на 5. Последняя цифра может быть 0 или 5. Рассмотрим оба случая:
   • Последняя цифра 0: Число имеет вид $A760$. Сумма цифр: $A + 7 + 6 + 0 = A + 13$. Для делимости на 3: $A + 13 \equiv 0 \pmod{3} \Rightarrow A \equiv 2 \pmod{3}$. Возможные значения: 2, 5, 8. Получаем числа: 2760, 5760, 8760.
   • Последняя цифра 5: Число имеет вид $A765$. Сумма цифр: $A + 7 + 6 + 5 = A + 18$. Для делимости на 3: $A + 18 \equiv 0 \pmod{3} \Rightarrow A \equiv 0 \pmod{3}$. Возможные значения: 3, 6, 9. Получаем числа: 3765, 6765, 9765.
   Ответ: 2760, 5760, 8760, 3765, 6765, 9765.
2. Представьте число 276 в виде суммы трёх слагаемых $a$, $b$, $c$, где $a : b = \frac{1}{3}$, $b : c = \frac{6}{5}$.
   Решение: Из условий: \[ a = \frac{1}{3}b, \quad c = \frac{5}{6}b \] Сумма: \[ \frac{1}{3}b + b + \frac{5}{6}b = \frac{13}{6}b = 276 \Rightarrow b = \frac{276 \cdot 6}{13} = \frac{1656}{13} = 127\frac{5}{13} \] Тогда: \[ a = \frac{1}{3} \cdot 127\frac{5}{13} = 42\frac{6}{13}, \quad c = \frac{5}{6} \cdot 127\frac{5}{13} = 106\frac{2}{13} \] Ответ: $a = 42\frac{6}{13}$, $b = 127\frac{5}{13}$, $c = 106\frac{2}{13}$.
3. Саша заказал пиццу диаметром 30 см, затем сменил заказ на пиццу диаметром 40 см. На сколько процентов увеличилась площадь пиццы?
   Решение: Площадь пиццы диаметром 30 см: \[ S_1 = \pi \left(\frac{30}{2}\right)^2 = 225\pi \text{ см}^2 \] Площадь пиццы диаметром 40 см: \[ S_2 = \pi \left(\frac{40}{2}\right)^2 = 400\pi \text{ см}^2 \] Увеличение площади: \[ \frac{400\pi - 225\pi}{225\pi} \cdot 100% = \frac{175}{225} \cdot 100% = \frac{700}{9}% = 77\frac{7}{9}\% \] Ответ: На $77\frac{7}{9}\%$.
4. Разрежьте фигуру на 4 равные по форме и площади части. Ответ: Разрезать фигуру на четыре одинаковые части, симметричные относительно центра (например, двумя перпендикулярными разрезами через центр).
5. Решите уравнение: $|x + 2{,}5| = 1$.
   Решение: \[ x + 2{,}5 = 1 \Rightarrow x = -1{,}5 \] или \[ x + 2{,}5 = -1 \Rightarrow x = -3{,}5 \] Ответ: $-1{,}5$; $-3{,}5$.
6. За 9 кг яблок заплатили столько же, сколько за $7{,}2$ кг бананов. Сколько стоит 1 кг каждого вида фруктов, если 2 кг бананов дороже 2 кг яблок на 40 рублей?
   Решение: Пусть цена яблок — $x$ руб/кг, бананов — $y$ руб/кг. Система: \[ \begin{cases} 9x = 7{,}2y \\ 2y - 2x = 40 \end{cases} \] Из первого уравнения: $x = 0{,}8y$. Подставим во второе: \[ 2y - 2 \cdot 0{,}8y = 40 \Rightarrow 0{,}4y = 40 \Rightarrow y = 100 \Rightarrow x = 80 \] Ответ: Яблоки — 80 руб/кг, бананы — 100 руб/кг.
7. Охотник со сворой собак едет в город на лошади со скоростью 12 км/ч. Каждые полчаса он отпускает одну собаку — она бежит в город со скоростью 15 км/ч. Сколько времени (в минутах) проходит между прибежавшими подряд собаками?
   Решение: Разница в расстоянии между последовательными собаками: \[ 12 \cdot 0{,}5 = 6 \text{ км} \] Время сокращения расстояния собакой: \[ \frac{6}{15 - 12} = 2 \text{ часа} = 120 \text{ минут} \] Но каждая следующая собака стартует через 30 минут. Разница во времени прибытия: \[ 30 - \frac{6}{15} \cdot 60 = 30 - 24 = 6 \text{ минут} \] Ответ: 6 минут.