Школа «Интеллектуал» из 6 в 7 класс 2021 год вариант 1-1

7 класс. Математика. Задание по выбору. 20 баллов.

Серия «В путь!»

1. Задача 1. В 10:00 Вася Куролесов вышел из города Карманова, а гражданин Лошаков — из города Курска. Между городами расстояние 18 км. Они пошли по одной дороге навстречу друг другу, Вася со скоростью 5 км/ч, а гражданин Лошаков — 4 км/ч. Они встретились в деревне Гадюкино и пошли дальше. Дойдя до Курска, Вася тут же развернулся и пошел обратно той же дорогой. Дойдя до Карманова, Лошаков сделал то же самое. Второй раз они встретились в деревне Ёжово.
   1. {1 балл} В котором часу они были в деревне Гадюкино?
      
   2. {1 балл} На каком расстоянии эта деревня от Курска?
      
   3. {1 балл} В котором часу они были в деревне Ежово?
      
   4. {1 балл} На каком расстоянии эта деревня от Карманова?
      
   
   
   
2. Задача 2. {3 балла} Два парохода вышли из пунктов $A$ и $B$ на озере навстречу друг другу. Первый раз они встретились на расстоянии $a$ км от пункта $A$. Продолжив движение, они прибыли в пункты $B$ и $A$ соответственно и тут же пошли обратно. Второй раз они встретились на расстоянии $b$ км от пункта $B$. Найдите расстояние между $A$ и $B$.
   

Серия «Бутерброды»

1. {1 балл} Петя принёс в школу прямоугольный кусок пирога. Сколькими способами можно разделить его пополам (по прямой линии от края до края)?
   
2. {2 балла} На следующий день Петя принёс в школу бутерброд — прямоугольный кусок хлеба с круглым куском колбасы, который лежал в углу хлеба. Сколькими способами можно разделить его пополам (по прямой линии от края до края)? Нужно порезать пополам и хлеб, и колбасу.
   
   
   
   
   
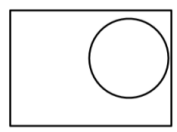
3. {3 балла} Через день Петя принёс в школу продвинутый бутерброд — прямоугольный кусок хлеба с круглым куском колбасы и квадратным куском сыра, которые лежали в разных углах хлеба. Сколькими способами можно разделить его пополам (по прямой линии от края до края)? Нужно порезать пополам и хлеб, и колбасу, и сыр.
   

Серия «Все прямоугольники»

1. {1 балл} Сколько существует различных прямоугольников площади 12, длины сторон которых являются целыми числами?
   
2. {1 балл} Сколько существует различных прямоугольников площади 100, длины сторон которых являются целыми числами?
   
3. {2 балла} Сколько существует различных прямоугольников площади 1000, длины сторон которых являются целыми числами?
   
4. {3 балла} Сколько существует различных прямоугольников площади 1440, длины сторон которых являются целыми числами?
   

Решения задач

1. Задача 1.
   1. Время встречи в Гадюкино:
      Общая скорость сближения: $5 + 4 = 9$ км/ч.
      Время до встречи: $\frac{18}{9} = 2$ часа.
      Встреча произошла в $10:00 + 2$ часа = $\boxed{12:00}$.
   2. Расстояние от Курска до Гадюкино:
      Гражданин Лошаков шёл $2$ часа со скоростью $4$ км/ч:
      $2 \cdot 4 = 8$ км.
      Ответ: $\boxed{8}$ км.
   3. Время встречи в Ёжово:
      После первой встречи до разворота они проходят весь путь до конечных пунктов и начинают движение обратно. Новое расстояние для сближения: $2 \cdot 18 = 36$ км.
      Время до второй встречи: $\frac{36}{9} = 4$ часа.
      Вторая встреча: $\boxed{16:00}$.
   4. Расстояние Ёжово от Карманова:
      От первой встречи Вася прошёл $5 \cdot 4 = 20$ км.
      Из них $10$ км до Курска и $10$ км обратно. За $4$ часа обратно он прошёл $10$ км, значит Еживо находится за $\boxed{6}$ км от Карманова.
2. Задача 2.
   При первой встрече пройденные расстояния: $a$ и $S - a$. После возвращения пройдённые расстояния до второй встречи: $S - b$ и $S + b$. Отношение скоростей сохраняется:
   $\frac{a}{S - a} = \frac{S + b}{S - b}$.
   Решая уравнение, получим $S = \boxed{3a - b}$.
3. Серия «Бутерброды».
   1. Деление прямоугольного пирога пополам:
      Любая прямая, проходящая через центр прямоугольника, делит его на две равные части. Количество способов — бесконечно.
      Ответ: $\boxed{\infty}$.
   2. Бутерброд с колбасой:
      Колбаса находится в углу. Единственная прямая, делящая пополам и хлеб, и колбасу — диагональ прямоугольника через центр колбасы и центр хлеба.
      Ответ: $\boxed{1}$ способ.
   3. Бутерброд с колбасой и сыром:
      Центры колбасы и сыра расположены в противоположных углах. Прямая диагонали через центр хлеба делит все компоненты пополам.
      Ответ: $\boxed{1}$ способ.
4. Серия «Все прямоугольники».
   1. Площадь 12:
      Пары $(a, b)$: $(1, 12)$, $(2, 6)$, $(3, 4)$.
      Ответ: $\boxed{3}$.
   2. Площадь 100:
      Пары: $(1, 100)$, $(2, 50)$, $(4, 25)$, $(5, 20)$, $(10, 10)$.
      Ответ: $\boxed{5}$.
   3. Площадь 1000:
      Число делителей: $16$. Пары: $\frac{16}{2} = 8$.
      Ответ: $\boxed{8}$.
   4. Площадь 1440:
      Число делителей: $36$. Пары: $\frac{36}{2} = 18$.
      Ответ: $\boxed{18}$.