Школа «Интеллектуал» из 6 в 7 класс 2015 год вариант 1-1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2015 год

Задача 1. Разрезания

Двумя прямолинейными разрезами разрежьте фигуру на наибольшее количество частей. Части между разрезами перекладывать запрещается. Части пронумеруйте. Ответ обведите в кружок. Рассматриваются три фигуры:

• Проволочная фигура
• Цельная фигура
• Цельная фигура с двумя круглыми дырками

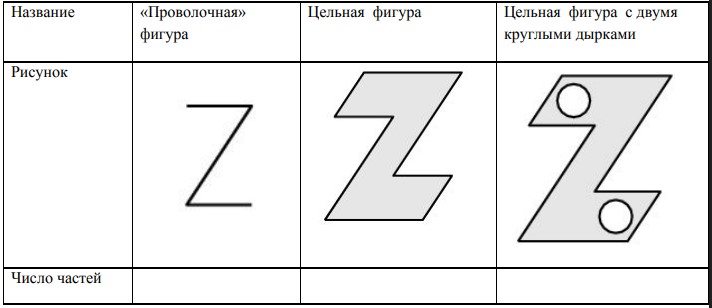
Число частей:

Задача 2. Таблица $3 \times 4$

1. Можно ли числа 1, 2, 3, ..., 12 расставить в таблицу из 3 строк и 4 столбцов так, чтобы сумма чисел в каждой из трёх строк была одинаковой?
   Если можно – покажите как. Если нельзя – объясните почему.
   
   
   
2. Можно ли те же числа расставить так, чтобы сумма чисел в каждом из 4 столбцов была одинаковой?
   Если можно – покажите как. Если нельзя – объясните почему.
   
   
   
3. Можно ли подобрать другие последовательные натуральные числа и расставить их в таблицу $3 \times 4$ так, чтобы суммы в столбцах были одинаковыми?
   Если можно – покажите как. Если нельзя – объясните почему.
   

Задача 3. Равенства

Даны равенства (на изображении — визуальный шаблон):

\[ 1 + 2 + 3 + 4 + 5 = 5 \cdot 3 \] \[ 2 + 3 + 4 + 5 + 6 = 5 \cdot 4 \] \[ 3 + 4 + 5 + 6 + 7 = 5 \cdot 5 \]

1. Напишите следующее равенство:
   
   
2. Напишите правило, по которому получаются равенства:
   
   
   
3. Объясните, почему это правило работает.
   Подсказка: воспользуйтесь формулой суммы арифметической прогрессии.
   

Решения задач

1. Разрезания
   
   Для каждой фигуры максимальное количество частей двумя разрезами:
   • Проволочная фигура (рамка): 7 частей. Пример разрезов: один разрез пересекает три стороны рамки, второй в другом направлении — аналогично.
   • Цельная фигура (квадрат): 4 части. Два пересекающихся разреза.
   • Фигура с дырками: 6 частей. Разрезы проходят через обе дырки, увеличивая количество деталей.
   
   
   Ответ: Проволочная — 7; Цельная — 4; С дырками — 6.
   
   
2. Таблица \(3 \times 4\)
   1. Да, можно. Пример расстановки: \[ \begin{array}{cccc} 12 & 1 & 2 & 11 \\ 10 & 3 & 4 & 9 \\ 8 & 5 & 6 & 7 \\ \end{array} \] Сумма каждой строки: 26.
      
      
   2. Нет. Общая сумма чисел от 1 до 12 равна 78. Для равных столбцов сумма каждого должна быть \(78/4 = 19,5\), что невозможно.
      
      
   3. Нет. Сумма \(n\) последовательных чисел равна \(S = \frac{(a_1 + a_n) \cdot n}{2}\). Для таблицы \(3 \times 4\) сумма 12 чисел должна делиться на 4. Но \(S = 12a_1 + 66\), и \(12a_1 + 66 \equiv 2 \mod 4\) для любого целого \(a_1\), что не делится на 4.
3. Равенства
   1. [А)] \(4 + 5 + 6 + 7 + 8 = 5 \cdot 6 = 30\)
      
      
   2. [Б)] Сумма пяти последовательных натуральных чисел равна \(5 \cdot \text{среднего числа}\) ряда.
      
      
   3. [В)] Формула суммы арифметической прогрессии: \(S = \frac{(a_1 + a_n) \cdot n}{2}\). Для пяти членов с разностью 1: \(a_n = a_1 + 4\). Средний член — \(a_3 = a_1 + 2\), тогда: \[ S = \frac{(a_1 + (a_1 + 4)) \cdot 5}{2} = \frac{(2a_1 + 4) \cdot 5}{2} = (a_1 + 2) \cdot 5 \] Таким образом, сумма действительно равна \(5 \cdot \) среднему члену.