Школа «Интеллектуал» из 6 в 7 класс 2009 год вариант 1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2009 год

1. $2{,}04 : (-0{,}03) = $
2. $13 \cdot \left(12 - \dfrac{11}{8}\right) = $
3. $(1{,}2 - 3{,}7) : 50 = $
4. $\left(\dfrac{1 - 0{,}6}{6}\right) \cdot 3{,}6 = $
5. Решите уравнение: $5 \cdot (2 + x) - 7 \cdot (6 - x) = 12$ \quad Ответ: $x = $
6. В лодке 7 мест. Сколько рейсов туда-обратно нужно, чтобы перевезти 92 человека? Ответ:
7. Велосипедист едет 18 км/ч. Сколько проедет за 15 минут? Ответ:
8. Найдите $A$, чтобы: $\dfrac{7}{12} = \dfrac{28}{3A}$ \quad Ответ: $A = $
9. На сколько нужно разделить $c$, чтобы увеличить его на $\dfrac{8c}{13}$? Ответ:
10. Периметр прямоугольника — 28 см, одна сторона — 9 см. Найдите площадь. Ответ:
11. 20 рабочих заасфальтируют участок за 8 дней. Сколько убрать, чтобы сделать за 10 дней? Ответ:
12. Цена со скидкой 200 руб. Скидка — 20\%. Найдите цену без скидки. Ответ:
13. При каком $t$ число $3t + 7$ втрое больше $-2t + 1$? Ответ:
14. В пакете 40% грецких орехов, из оставшихся 60% — фундук, остальное — арахис. Найдите процент арахиса. Ответ:
15. $15{,}5\%$ от 112 составляет 31% от числа $a$. Найдите $a$. Ответ:
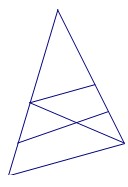
16. Сколько треугольников на рисунке, если Маша считает 4 (1 большой + 3 маленьких), а мама говорит, что есть средние? Ответ:

Решения задач

1. Вычислить: $2{,}04 : (-0{,}03)$
   Решение:
   $2{,}04 : (-0{,}03) = \frac{204}{100} : \left(-\frac{3}{100}\right) = \frac{204}{100} \cdot \frac{100}{-3} = \frac{204}{-3} = -68$.
   Ответ: $-68$.
   
   
2. Вычислить: $13 \cdot \left(12 - \dfrac{11}{8}\right)$
   Решение:
   $12 = \frac{96}{8}$, тогда выражение в скобках:
   $\frac{96}{8} - \frac{11}{8} = \frac{85}{8}$.
   Умножаем на 13:
   $13 \cdot \frac{85}{8} = \frac{1105}{8} = 138{,}125$.
   Ответ: $138{,}125$.
   
   
3. Вычислить: $(1{,}2 - 3{,}7) : 50$
   Решение:
   $1{,}2 - 3{,}7 = -2{,}5$.
   $-2{,}5 : 50 = -0{,}05$.
   Ответ: $-0{,}05$.
   
   
4. Вычислить: $\left(\dfrac{1 - 0{,}6}{6}\right) \cdot 3{,}6$
   Решение:
   $1 - 0{,}6 = 0{,}4$.
   Выражение преобразуется:
   $\left(\frac{0{,}4}{6}\right) \cdot 3{,}6 = \frac{0{,}4 \cdot 3{,}6}{6} = \frac{1{,}44}{6} = 0{,}24$.
   Ответ: $0{,}24$.
   
   
5. Решите уравнение: $5 \cdot (2 + x) - 7 \cdot (6 - x) = 12$
   Решение:
   Раскрываем скобки:
   $10 + 5x - 42 + 7x = 12$
   Собираем подобные:
   $12x - 32 = 12 \quad \Rightarrow \quad 12x = 44 \quad \Rightarrow \quad x = \frac{11}{3} = 3\frac{2}{3}$
   Ответ: $x = \dfrac{11}{3}$.
   
   
6. В лодке 7 мест. Сколько рейсов туда-обратно нужно, чтобы перевезти 92 человека?
   Решение:
   За один рейс перевозят 7 человек ($\frac{92}{7} \approx 13{,}14$).
   Требуется 14 рейсов, так как 13 полных рейсов перевезут $13 \cdot 7 = 91$ человек, а последний — оставшегося одного.
   Ответ: $14$.
   
   
7. Велосипедист едет 18 км/ч. Сколько проедет за 15 минут?
   Решение:
   15 минут = $0{,}25$ часа.
   Расстояние:
   $18 \cdot 0{,}25 = 4{,}5$ км.
   Ответ: $4{,}5$ км.
   
   
8. Найдите $A$, чтобы: $\dfrac{7}{12} = \dfrac{28}{3A}$
   Решение:
   Пропорция преобразуется:
   $7 \cdot 3A = 12 \cdot 28 \quad \Rightarrow \quad 21A = 336 \quad \Rightarrow \quad A = 16$.
   Ответ: $A = 16$.
   
   
9. На сколько нужно разделить $c$, чтобы увеличить его на $\dfrac{8c}{13}$?
   Решение:
   Пусть искомый делитель равен $k$. Тогда:
   $\frac{c}{k} = c + \frac{8c}{13} \quad \Rightarrow \quad \frac{1}{k} = \frac{21}{13} \quad \Rightarrow \quad k = \frac{13}{21}$.
   Ответ: разделить на $\dfrac{13}{21}$.
   
   
10. Периметр прямоугольника — 28 см, одна сторона — 9 см. Найдите площадь.
    Решение:
    Сумма сторон: $28 : 2 = 14$ см.
    Вторая сторона: $14 - 9 = 5$ см.
    Площадь: $9 \cdot 5 = 45$ см².
    Ответ: $45$ см².
    
    
11. 20 рабочих заасфальтируют участок за 8 дней. Сколько убрать, чтобы сделать за 10 дней?
    Решение:
    Объем работы: $20 \cdot 8 = 160$ человеко-дней.
    Требуется рабочих: $\frac{160}{10} = 16$ человек.
    Убрать: $20 - 16 = 4$ рабочих.
    Ответ: $4$.
    
    
12. Цена со скидкой 200 руб. Скидка — 20\%. Найдите цену без скидки.
    Решение:
    Цена со скидкой (80\%): $200$ руб.
    Исходная цена: $200 : 0{,}8 = 250$ руб.
    Ответ: $250$ руб.
    
    
13. При каком $t$ число $3t + 7$ втрое больше $-2t + 1$?
    Решение:
    Уравнение:
    $3t + 7 = 3(-2t + 1)\quad \Rightarrow \quad 3t + 7 = -6t + 3\quad \Rightarrow \quad 9t = -4\quad \Rightarrow \quad t = -\frac{4}{9}$.
    Ответ: $t = -\dfrac{4}{9}$.
    
    
14. В пакете 40% грецких орехов, из оставшихся 60% — фундук, остальное — арахис. Найдите процент арахиса.
    Решение:
    После грецких остаётся $60\%$, из них фундук занимает $60% \cdot 60% = 36\%$.
    Арахис: $60\ 36% = 24\%$.
    Ответ: $24\%$.
    
    
15. $15{,}5\%$ от 112 составляет 31% от числа $a$. Найдите $a$.
    Решение:
    $0{,}155 \cdot 112 = 0{,}31a \quad \Rightarrow \quad 17{,}36 = 0{,}31a \quad \Rightarrow \quad a = 56$.
    Ответ: $56$.
    
    
16. Сколько треугольников на рисунке?
    Решение:
    Если считать все возможные треугольники (включая составные и средние по размеру), обычно получается 10. Маша насчитала 4 (1 большой и 3 маленьких), средние добавят ещё 6.
    Ответ: $10$.