Школа «Интеллектуал» из 4 в 5 класс 2022 год вариант 1-1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2022 год

1. Сколько существует трёхзначных чисел, сумма цифр которых равна 3?
   Ответ:
   
   
2. Вася плывёт по реке. От деревни Васенки до деревни Березово, которые стоят на реке, он проплывает за 3 часа, а в обратную сторону — за 1 час. Известно, что расстояние между деревнями 6 км. Определите скорость течения реки и собственную скорость Васи в км/ч, считая, что эти скорости постоянны.
   Ответ:
   
   
3. В классе проводился зачёт. Сначала Маша взяла половину билетов, которые лежали на столе. Оля взяла половину оставшихся билетов. Аня взяла треть от того, что ещё лежало на столе. Для Саши осталось лишь 2 билета. Сколько билетов для зачёта лежало на столе изначально?
   Ответ:
   
   
4. Пираты играли в игру: складывали очень тонкий канат вдвое. После того как они сложили канат вдвое, они сложили его вдвое ещё раз, а потом ещё раз. Потом пришёл капитан, который разрубил канат поперёк одним ударом сабли. Оказалось, что канат распался на куски, длина двух из которых — 4 метра и 9 метров. Какая могла быть наименьшая длина первоначального каната? Ответ укажите в метрах.
   Ответ:
   
   
5. В метро на маленькой кольцевой линии работают три поезда, которые едут с одинаковой скоростью на одинаковом расстоянии друг от друга. Интервал прибытия поездов — 8 минут. С каким интервалом будут ходить поезда, если их станет 4?
   Ответ:
   
   
6. У Пети были фигуры конструктора, изображённые в первой строке. Он взял несколько из них и собрал новую фигуру. Укажите, какие фигуры из второй строки у него могли получиться.
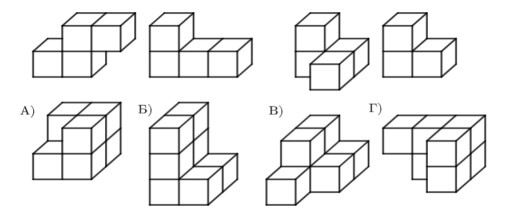   Ответ:

Решения задач

1. Сколько существует трёхзначных чисел, сумма цифр которых равна 3?
   Решение: Сумма цифр трёхзначного числа равна 3. Найдём все возможные комбинации цифр (с учётом порядка):
   • Комбинация 3,0,0: Единственное число — 300.
   • Комбинация 2,1,0: Числа 210, 201, 120, 102.
   • Комбинация 1,1,1: Число 111.
   Итого: $1 + 4 + 1 = 6$ трёхзначных чисел.
   Ответ: 6.
   
   
2. Определите скорость течения реки и собственную скорость Васи, если расстояние между деревнями 6 км, скорость по течению — 3 часа, против течения — 1 час.
   Решение: Пусть собственная скорость Васи $v$ (км/ч), скорость течения $u$ (км/ч). \begin{align} \begin{cases} v + u = \frac{6}{1} = 6 &\text{(по течению)}, \\ v - u = \frac{6}{3} = 2 &\text{(против течения)}. \end{cases} \end{align} Сложив уравнения: $2v = 8 \Rightarrow v = 4$ км/ч, тогда $u = 6 - 4 = 2$ км/ч.
   Ответ: скорость течения 2 км/ч, скорость Васи 4 км/ч.
   
   
3. Сколько билетов было изначально, если после Маши, Оли и Ани осталось 2 билета?
   Решение: Пусть изначально было $x$ билетов. \begin{align} &\text{Маша: } x \rightarrow \frac{x}{2} \quad \text{(остаток)}, \\ &\text{Оля: } \frac{x}{2} \rightarrow \frac{x}{4} \quad \text{(остаток)}, \\ &\text{Аня: } \frac{x}{4} \rightarrow \frac{x}{4} - \frac{x}{12} = \frac{x}{6} \quad \text{(остаток)}. \end{align} По условию $\frac{x}{6} = 2 \Rightarrow x = 12$.
   Ответ: 12.
   
   
4. Наименьшая длина первоначального каната при трёх сложениях вдвое.
   Решение: После трёх сложений канат имеет 8 слоёв. При разрезании его распадается на куски длиной $8x$ и $8y$, где $x + y = \frac{L}{8}$. Из условия $8x = 4$ и $8y = 9$ (или наоборот) минимальная длина:
   $ L = 4 + 9 = 13 \text{ метров}. $
   Ответ: 13.
   
   
5. Интервал движения поездов при увеличении их количества с трёх до четырёх.
   Решение: При трёх поездах интервал $T = 8$ мин. Время полного круга: $3T = 24$ мин. Для четырёх поездов интервал: $$ \frac{24}{4} = 6 \text{ минут}. $$
   Ответ: 6 минут.
   
   
6. Фигуры, которые можно собрать из исходных элементов.
   Ответ: А, Б, Г.