Школа «Интеллектуал» из 4 в 5 класс 2020 год вариант 1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2020 год

1. Автомат делит чётное число пополам, а к нечётному прибавляет 5. Известно, что за три шага автомат получил из натурального нечётного числа $N$ число 5.
   
   Найдите сумму цифр числа $N$.
   
   Ответ:
   
   
2. Чему равно выражение $10000 \cdot \text{AROO} - 10000 \cdot \text{KANG} + \text{KANGAROO}$, если разные буквы обозначают разные цифры? Обведите правильный ответ:
   1. AROOAROO
   2. AROOKANG
   3. KANGKANG
   4. KANGAROO
   5. ARKANGOO
   
   
   
3. Пять джентльменов: A, B, C, D и E встретились в клубе. Некоторые из них приветствовали друг друга рукопожатиями. При этом A и B пожали руку по одному разу, а C, D и E — по два раза. Известно, что A пожал руку E. Какого рукопожатия наверняка не было? Обведите правильный ответ.
   
   
   1. C – D
   2. C – E
   3. B – E
   4. B – D
   5. B – C
   
   
   
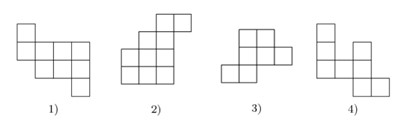
4. Из листа клетчатой бумаги вырезали два кусочка. В результате образовалась дыра, изображённая на рисунке. Найдите вырезанные кусочки среди фигур 1) — 4).
   а) Нарисуйте, как они располагались в дыре, заштриховав их так, чтобы кусочки отличались.
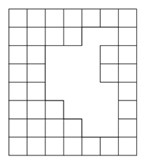   б) Укажите номера нужных кусочков.
   Ответ:
   
   
5. а) Незнайка выстроил из 63 кубиков шесть башенок в ряд, причём количество кубиков в каждых двух соседних башенках отличается на один. Прав ли он?
   
   Если да, расскажите, какие башенки он построил.
   [2ex] Если нет, объясните, почему вы так думаете.
   [2ex]
   
   
6. б) Из 63 кубиков Шпунтик построил восемь башенок в ряд, причём он утверждает, что и в его постройке количество кубиков в каждых двух соседних башенках отличается на один. Прав ли он?
   
   Если да, расскажите, какие башенки он построил.
   [2ex] Если нет, объясните, почему вы так думаете.
   [2ex]

Решения задач

1. Автомат делит чётное число пополам, а к нечётному прибавляет 5. Известно, что за три шага автомат получил из натурального нечётного числа $N$ число 5. Найдите сумму цифр числа $N$.
   Решение: Работаем «обратным ходом». Последний шаг дал число 5. Чтобы получить 5 в третьем шаге, предыдущее число должно быть чётным — делением на 2: $5 \cdot 2 = 10$.
   На втором шаге получили 10. Возможные варианты предыдущего числа:
   • $10 \cdot 2 = 20$ (чётное)
   • $10 - 5 = 5$ (нечётное, но переначальное число натуральное)
   Проверяем первый вариант: исходное число 20 ⇒ число перед третьим шагом 10. Тогда на первом шаге было $20$ (чётное) ⇒ до шага 1: $20 \cdot 2 = 40$ (чётное, противоречит нечётному $N$). Не подходит. Второй вариант: перед третьим шагом число $5$ не подходит, так как для нечётного числа шаг — прибавление 5, $5 - 5 = 0$ (не натуральное). Возвращаемся ко второму шагу. Если вторым шагом получено 10 из предыдущего действия автомата, то до второго шага могло быть $5$ (нечётное +5). Тогда до второго шага: $5$, что получено из $N$:
   • Если число перед вторым шагом — чётное ⇒ $5 = N / 2 ⇒ N = 10$ (чётное, не подходит).
   • Если число нечётное ⇒ $5 = N + 5 ⇒ N = 0$ (невозможно).
   Следовательно, единственная корректная траектория:
   Шаг 1: $15 + 5 = 20$
   Шаг 2: $20 / 2 = 10$
   Шаг 3: $10 / 2 = 5$
   Исходное число $N = 15$, сумма цифр: $1 + 5 = 6$.
   Ответ: 6.
2. Чему равно выражение $10000 \cdot \text{AROO} - 10000 \cdot \text{KANG} + \text{KANGAROO}$, если разные буквы обозначают разные цифры?
   Решение: Заметим, что $\text{KANGAROO} = 10000 \cdot \text{KANG} + \text{AROO}$. Подставив это в выражение: \[ 10000 \cdot \text{AROO} - 10000 \cdot \text{KANG} + (10000 \cdot \text{KANG} + \text{AROO}) = 10000 \cdot \text{AROO} + \text{AROO} = \text{AROO} \times 10001. \] Учитывая, что $\text{AROO}$ — четырёхзначное число, умножение на $10001$ даёт число $\text{AROOAROO}$. Это соответствует варианту а).
   Ответ: $\boxed{а)}$.
3. Пять джентльменов A, B, C, D, E встретились в клубе. A и B пожали руку по одному разу, C, D, E — по два раза. Известно, что A пожал руку E. Какое рукопожатие наверняка не произошло?
   Решение: Общее количество рукопожатий: $\frac{1 + 1 + 2 + 2 + 2}{2} = 4$. A участвовал в одном рукопожатии (c E). E должен пожать ещё одну руку (например, C или D). B может пожать руку только одному — но если B пожмёт E, то E станет обладателем трёх рукопожатий (противоречие). Аналогично: если B пожмёт C или D, это приведёт к превышению допустимого количества рукопожатий C/D. Единственная возможность без противоречий — B пожал руку D или C, но в любом случае рукопожатие B–C невозможно, так как C должен пожать дважды.
   Ответ: $\boxed{е)}$.
4. Из листа клетчатой бумаги вырезали два кусочка. Найдите вырезанные кусочки среди фигур 1) — 4).
   Решение: a) Проанализировав отверстие, можно заметить, что её форма соответствует комбинации фигур 2) и 3). Их расположение: фигура 2) расположена слева горизонтально, фигура 3) — справа вертикально.
   б) Номера вырезанных кусков: 2) и 3).
   Ответ: $\boxed{2}$ и $\boxed{3}$.
5. a) Незнайка выстроил из 63 кубиков шесть башенок в ряд, причём количество кубиков в каждых двух соседних башенках отличается на один. Прав ли он?
   Решение: Пусть первая башенка содержит $a$ кубиков. Тогда ряд можно представить как $a, a+1, a+2, a+3, a+4, a+5$. Сумма: \[ 6a + (0 + 1 + 2 + 3 + 4 + 5) = 6a + 15 = 63 \⇒ 6a = 48 \⇒ a = 8. \] Последовательность: $8, 9, 10, 11, 12, 13$. Сумма: $8 + 9 + 10 + 11 + 12 + 13 = 63$.
   Ответ: Да, последовательность: 8, 9, 10, 11, 12, 13.
6. б) Шпунтик построил восемь башенок в ряд из 63 кубиков, утверждая, что количество кубиков в соседних башенках отличается на один. Прав ли он?
   Решение: Предположим последовательность вида $a, a+1, a-1, a, a+1, a-1, \ldots$. Сумма произвольной последовательности такого вида будет кратно нечётному числу кубиков в мере. Для восьми членов сумма обязательно чётная, так как количество чётных и нечётных элементов чередуется. Сумма 63 нечётна ⇒ построить невозможно.
   Ответ: Нет, суммативн кусoбражаетоё общества.