8 800 707 6729
8 800 707 6729Telegram канал

Школа «Интеллектуал» из 4 в 5 класс 2019 год вариант 1

Сложность:
Дата экзамена: 2019
Сложность:
Дата экзамена: 2019
youit.school ©

ШКОЛА "ИНТЕЛЛЕКТУАЛ"


2019 год




  1. Автомат делит чётное число пополам, а к нечётному прибавляет 5. Известно, что за три шага автомат получил из натурального нечётного числа $N$ число 5.
    Найдите сумму цифр числа $N$.
    Ответ:

  2. Чему равно выражение $10000 \cdot \text{AROO} - 10000 \cdot \text{KANG} + \text{KANGAROO}$, если разные буквы обозначают разные цифры? Обведите правильный ответ:
    1. AROOAROO
    2. AROOKANG
    3. KANGKANG
    4. KANGAROO
    5. ARKANGOO


  3. Пять джентльменов: A, B, C, D и E встретились в клубе. Некоторые из них приветствовали друг друга рукопожатиями. При этом A и B пожали руку по одному разу, а C, D и E — по два. Известно, что A пожал руку E. Какого рукопожатия точно не было? Обведите правильный ответ:
    1. C – D
    2. C – E
    3. B – E
    4. B – D
    5. B – C


  4. Целые числа от 1 до 7 вписывают по одному в кружки на рисунке так, чтобы суммы чисел в каждой тройке кружков, расположенных на прямой линии, были одинаковыми, а цифры в кружках не повторялись. Запишите все возможные цифры, которые могут стоять в центральном кружке.
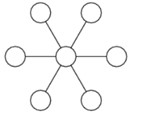    Ответ:

  5. В прямоугольнике размером $300 \times 200$ клеток, нарисованном на клетчатой бумаге, проведена диагональ. Сколько клеточек она разрезала?
    Ответ:

  6. Один из нарисованных кубиков не может иметь развёртки, изображённой на левом рисунке. Какой? Укажите соответствующую букву.
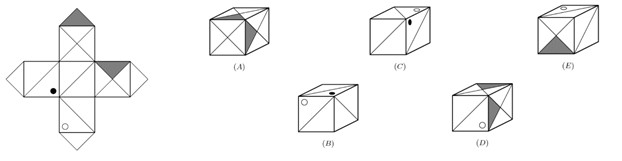    Ответ:

  7. В одном австралийском городе на площади стоит памятник Кенгуру. К этой площади ведут шесть улиц. По четырём из них разрешено двустороннее движение, а по двум — одностороннее, по направлению к площади. Турист на автомобиле собирается приехать на площадь, посмотреть памятник, а затем покинуть её. Сколько различных маршрутов он может для этого построить?
    Ответ:

  8. Из листа клетчатой бумаги вырезали два кусочка. В результате образовалась дыра, изображённая на рисунке. Найдите вырезанные кусочки среди фигур 1) — 4).
    а) Нарисуйте, как они располагались в дыре, заштриховав их так, чтобы кусочки отличались.
    б) Укажите номера нужных кусочков.
    Ответ:

  9. На столе лежит длинная полоска бумаги, разделённая на 2000 одинаковых равносторонних треугольников. Правый край полоски закреплён. Полоску складывают по линиям, «наматывая» на треугольник $ABC$: сначала по $BC$, затем по $CD$ и т.д.
    В каком положении окажутся точки $A$, $B$ и $C$ после 1999 шагов? Обведите правильный ответ.
    Ответ:

  10. Король хочет построить шесть крепостей и соединить каждую пару крепостей дорогой (всего 15 дорог), не проходящих через другие крепости.
    Нарисуйте такую схему расположения крепостей и дорог, чтобы на ней было только три перекрёстка, и на каждом из них пересекались ровно две дороги.
    Ответом является нарисованная схема.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Автомат делит чётное число пополам, а к нечётному прибавляет 5. Известно, что за три шага автомат получил из натурального нечётного числа $N$ число 5. Найдите сумму цифр числа $N$.
    Решение: Разберём действия автомата в обратном порядке:
    • Шаг 3: Чтобы получить 5, предыдущее число должно быть 10 ($10/2 = 5$, т.к. 5 чётно).
    • Шаг 2: Число 10 могло получиться из 20 ($20/2 = 10$) или из 5 ($5 + 5 = 10$). Последнее исключено, так как 0 не натуральное.
    • Шаг 1: Число 20 получается только из $N + 5 = 20$ (деление пополам цепочек достаточно). Тогда $N = 15$.
    Сумма цифр числа 15: $1 + 5 = 6$.
    Ответ: 6.

  2. Чему равно выражение $10000 \cdot \text{AROO} - 10000 \cdot \text{KANG} + \text{KANGAROO}$, если разные буквы обозначают разные цифры?
    Решение: Разберём указанную структуру: \begin{align*} &\text{KANGAROO} = \text{KANG} \cdot 10000 + \text{AROO}, \\ &\text{Выражение} = \text{AROO} \cdot 10000 - \text{KANG} \cdot 10000 + \text{KANGAROO} = \text{KANGAROO}. \end{align*} Ответ: (d) KANGAROO.

  3. Пять джентльменов: A, B, C, D и E встретились в клубе. A и B пожали руку по одному разу, а C, D и E — по два. A пожал руку E. Какого рукопожатия точно не было?
    Решение:
    • Всего рукопожатий: $(1+1+2+2+2)/2 = 4$ (каждое рукопожатие учтено дважды).
    • A имеет рукопожатия: E и ещё кому-то (?). Чтобы сумма рукопожатий B была равна 1, B не может иметь рукопожатий с C, D или E без превышения.
    Ответ: (e) B – C.

  4. Целые числа от 1 до 7 вписывают в кружки так, чтобы суммы чисел в каждой тройке были одинаковыми. Центральное число:
    Решение: Сумма всех чисел в кругах: $1+2+...+7=28$. Каждая тройка учитывает центральное число трижды. Пусть сумма тройки $S$, тогда центральное число $4$:
    $28 + 2x = 4S$ → $\frac{28 + 2x}{4} = S$, где $x$ — центральное число. Возможные значения $x$ — 4.
    Ответ: 4.

  5. В прямоугольнике $300 \times 200$ клеток проведена диагональ. Сколько клеток она разрезала?
    Решение: По формуле пересечения диагональю клеток: $N = 300 + 200 - \text{НОД}(300,200) = 500 - 100 = 400$.
    Ответ: 400.

  6. Какой кубик не соответствует развёртке? Анализ сеток показывает несопоставимые грани для куба B.
    Ответ: B.

  7. Турист может выбрать 4 двусторонние и 2 односторонние улицы:
    • Въезд: $4 \times 2 = 8$ вариантов (по двусторонним + односторонние),
    • Выезд: аналогично,
    • Итого: $8 \times 8 = 64$ маршрута.
    Ответ: 64.

  8. а) Вырезанные кусочки 1 и 3 образуют дыру. б) Номера 1 и 3.
    Ответ: б) 1, 3.

  9. Складывание полоски по треугольника приводит к циклическому вращению через 6 шагов. Остаток $1999 \mod 6 = 1$. После первого шага C перемещается вверх → положение аналогично начальному с поворотом.
    Ответ: Все точки вернутся в исходное положение.

  10. Пример схемы с тремя перекрёстками:
    (Схема приводится в виде рисунка, демонстрирующего крепости и дороги с тремя пересечениями).
Материалы школы Юайти