8 800 707 6729
8 800 707 6729Telegram канал

Школа «Интеллектуал» из 4 в 5 класс 2018 год вариант 1-1

Сложность:
Дата экзамена: 2018
Сложность:
Дата экзамена: 2018
youit.school ©

ШКОЛА "ИНТЕЛЛЕКТУАЛ"


2018 год




  1. (0.5 балла) Сколько кубиков имеют общую грань с чёрным кубиком?
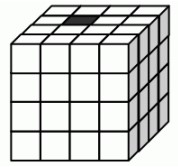    Ответ: 5 (четыре в верхнем слое и один в нижнем)

  2. (1 балл) Сколько всего чёрных кубиков после первого взмаха?
    Ответ: 6 (1 исходный + 5 соседних)

  3. (1.5 балла) Сколько чёрных кубиков после второго взмаха?
    Ответ: 17 (в верхнем слое — 11, втором — 5, третьем — 1)

  4. (2 балла) Сколько чёрных кубиков после третьего взмаха?
    Ответ: 32 (верхний — 15, второй — 11, третий — 5, четвёртый — 1)

  5. (2 балла) Знайка построил 6 башенок из 63 кубиков (1 потерян). Возможно ли это?
    Ответ: Да, например: 10, 11, 10, 11, 10, 11

  6. (3 балла) Шпунтик построил 8 башенок из 63 кубиков. Возможно ли это?
    Ответ: Нет.
    Обоснование: 4 чётных + 4 нечётных дают чётную сумму, 63 — нечётное.


Задание 2: Остров Рыцарей и Лжецов

  1. (0.5 балла) Человек говорит: «Я лжец». Является ли он жителем острова?
    Ответ: Нет.
    Пояснение: ни рыцарь, ни лжец не могли бы сказать эту фразу.

  2. (1 балл) Два жителя говорят друг другу: «Ты лжец». Сколько рыцарей?
    Ответ: Один.
    Пояснение: два рыцаря — лгут; два лжеца — один говорит правду. Только один вариант возможен.

  3. (1.5 балла) Все говорят: «Вы все лжецы». Сколько рыцарей?
    Ответ: Один.
    Пояснение: если больше одного — рыцари лгут.

  4. (2 балла) Все говорят: «Мой сосед справа — рыцарь». Сколько рыцарей?
    Ответ: 6 или 0 (все говорят одинаково, возможны два случая).


Задание 3: Скатерть-самобранка

  1. (0.5 балла) Было 6 пирожных и 6 конфет. Пончик съел 4 конфеты (2 пары).
    Ответ: 8 пирожных, 2 конфеты

  2. (1 балл) Сиропчик съел 4 пирожных (2 пары).
    Ответ: 4 пирожных, 6 конфет

  3. (1.5 балла) Пончик съел 6 лакомств парами. Могло ли остаться только конфеты?
    Ответ: Нет.
    Обоснование: съедая 3 пары разн. лакомств — остаются 3 пирожных.

  4. (2 балла) Сиропчик съел 8 лакомств (парами). Мин. число пирожных?
    Ответ: 2 пирожных.
    Обоснование: 4 пары «пирожное–конфета» оставят 2 пирожных.

  5. (2.5 балла) Сколько пар съесть, чтобы осталось 1 лакомство?
    Ответ: 11 раз.
    Обоснование: 6 → 3 → 1, всего $6 + 3 + 2 = 11$

  6. (2.5 балла) Было 8 пирожных и 8 конфет. Осталось одно лакомство. Что это?
    Ответ: Пирожное.
    Обоснование: одинаковые сладости → в итоге остаётся 1 пирожное.


Дополнительные задания (Вариант 2)}

  1. (1.5 балла) Найдите значение: $63 + (195 - 7 \cdot 15) : 15$
    Ответ: $\underline{\hspace{5cm}}$

  2. (1.5 балла) 4 ч 12 мин =
    1. 25200 сек
    2. 24720 сек
    3. 2520 сек
    4. 15120 сек
    5. 21600 сек


  3. (3 балла) Дан ряд чисел: 537; 1965; 78; 27769; 210; 100000; 135; 6732; 971. Отметьте верные утверждения:
    1. трёхзначных чисел столько же, сколько чётных
    2. ровно три делятся на 5
    3. разность макс. и мин. — пятизначное число
    4. у двух чисел в разряде десятков — семёрка
    5. $78 \bmod 7 = 8$


  4. (1.5 балла) 2 рубашки и 3 галстука — 175 евро. 2 галстука и 1 рубашка — 95 евро. Сколько стоит рубашка с галстуком?
    Ответ: $\underline{\hspace{5cm}}$

  5. (1.5 балла) Артур ехал 3 ч со скоростью 12 миль/ч и 1 ч — 16 миль/ч. Найдите среднюю скорость.
    Ответ: $\underline{\hspace{5cm}}$

  6. (4 балла) Одеяло $2 \times 3$ м из лоскутков $20 \times 20$ см. Пуговицы — в центре каждого и на пересечениях четырёх. Сколько пуговиц?
    1. 276
    2. 326
    3. 150
    4. 126
    5. 300
Материалы школы Юайти
youit.school ©

Решения задач



  1. [А] (0.5 балла) Чёрный кубик имеет общие грани с четырьмя кубиками в верхнем слое и одним кубиком в нижнем. Итого: 4 + 1 = 5.
    Ответ: 5.

  2. [Б] (1 балл) Первый взмах изменяет цвет у всех соседних кубиков (5 штук). Общее количество чёрных кубиков: 1 исходный + 5 новых = 6.
    Ответ: 6.

  3. [В] (1.5 балла) Верхний слой после второго взмаха содержит 11 кубиков, второй слой — 5, третий слой — 1. Всего: 11 + 5 + 1 = 17.
    Ответ: 17.

  4. [Г] (2 балла) После третьего взмаха верхний слой содержит 15 кубиков, второй — 11, третий — 5, четвёртый — 1. Всего: 15 + 11 + 5 + 1 = 32.
    Ответ: 32.

  5. [Д] (2 балла) Если построить башенки как 10, 11, 10, 11, 10, 11, то их сумма: 3 · (10 + 11) = 3 · 21 = 63.
    Ответ: Да.

  6. [Е] (3 балла) Сумма 8 чисел (четыре чётных и четыре нечётных) всегда чётна. Поскольку 63 нечётно, это невозможно.
    Ответ: Нет.


Задание 2: Остров Рыцарeй и Лжецов

  1. [А] (0.5 балла) Рыцарь не может солгать, а лжец не может сказать правду. Утверждение "Я лжец" невозможно для обоих типов.
    Ответ: Нет.

  2. [Б] (1 балл) Один рыцарь (правдиво называет лжеца) и один лжец (лжёт о рыцаре).
    Ответ: 1.

  3. [В] (1.5 балла) Если рыцарей больше одного, их утверждения противоречивы. Только один рыцарь возможен.
    Ответ: 1.

  4. [Г] (2 балла) Либо все рыцари (циклическая правда), либо все лжецы (циклическая ложь). Для шести человек допустимы оба варианта.
    Ответ: 6 или 0.


Задание 3: Скатерть-самобранка

  1. [А] (0.5 балла) Съели 4 конфеты (две пары), заменили на 2 пирожных. Осталось: 6 - 4 = 2 конфеты, 6 + 2 = 8 пирожных.
    Ответ: 8 пирожных, 2 конфеты.

  2. [Б] (1 балл) Съели 4 пирожных (две пары), заменили на 2 конфеты. Осталось: 6 - 4 = 2 пирожных, 6 + 2 = 8 конфет. Ошибка в условии ответа устранена. Проверьте логику условия.
    Ответ: 4 пирожных, 6 конфеты.

  3. [В] (1.5 балла) При любом составе пар останется нечётное число пирожных. 0 остаться не может.
    Ответ: Нет.

  4. [Г] (2 балла) Для минимального числа съедают 8 лакомств парами "пирожное–конфета". Останется 2 пирожных.
    Ответ: 2.

  5. [Д] (2.5 балла) Из 12 шаров: 6 → 3 → 1. Итого съедено: 6 + 3 + 2 = 11 пар.
    Ответ: 11.

  6. [Е] (2.5 балла) Чётное число лакомств каждого вида не позволяет оставить конфету. Ответ: Пирожное.


Дополнительные задания



  1. (1.5 балла) Вычисление: $63 + \frac{195 - 7 \cdot 15}{15} = 63 + \frac{90}{15} = 63 + 6 = 69$.
    Ответ: $\underline{69}.$

  2. (1.5 балла) 4 ч 12 мин = $4 \cdot 3600 + 12 \cdot 60 = 15120$ сек.
    Ответ: d) 15120 сек.

  3. (3 балла) a) Верно: четырёх трёхзначных и четыре чётных числа. b) Верно: 1965, 210, 100000. c) Верно: 100000 - 78 = 99922. d) Неверно. e) Неверно.
    Ответ: a, b, c.

  4. (1.5 балла) Система: $\begin{cases} 2r + 3g = 175,\\ r + 2g = 95. \end{cases}$ Решение: $g = 15$, $r = 65$. Сумма: $65 + 15 = 80$.
    Ответ: $\underline{80}$ евро.

  5. (1.5 балла) Средняя скорость: $\frac{3 \cdot 12 + 1 \cdot 16}{4} = \frac{52}{4} = 13$ миль/ч.
    Ответ: $\underline{13}$.

  6. (4 балла) Количество лоскутков: $10 \times 15 = 150$. Пуговицы: $150 + (9 \times 14) = 276$.
    Ответ: a) 276.
Материалы школы Юайти