Школа «Интеллектуал» из 4 в 5 класс 2018 год вариант 1

ШКОЛА "ИНТЕЛЛЕКТУАЛ"

2018 год

1. (0.5 балла) Сколько маленьких кубиков имеют общую грань с чёрным кубиком?
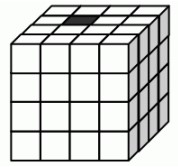   Ответ: ___________________
   
   
2. (1 балл) Сколько всего получилось чёрных кубиков после первого взмаха?
   Ответ: ___________________
   
   
3. (1.5 балла) Сколько всего получилось чёрных кубиков после второго взмаха?
   Ответ: ___________________
   
   
4. (2 балла) Сколько всего получилось чёрных кубиков после третьего взмаха?
   Ответ: ___________________
   
   
5. (2 балла) Знайка выстроил из этих кубиков 6 башенок в ряд, количество кубиков в соседних отличается на 1. Говорит, что потерял 1 кубик (всего 63). Может ли такое быть?
   Ответ: ___________________
   Обоснование: \underline{\hspace{\linewidth}}
   
   
6. (3 балла) Шпунтик построил 8 башенок из 63 кубиков, с разностью 1 у соседних. Может ли такое быть?
   Ответ: ___________________
   Обоснование: \underline{\hspace{\linewidth}}

Задание 2

На Острове живут рыцари (всегда правдивы) и лжецы (всегда лгут).

1. (0.5 балла) Человек говорит: «Я лжец». Является ли он жителем Острова?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
2. (1 балл) Два жителя сказали друг другу: «Ты лжец». Сколько среди них рыцарей?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
3. (1.5 балла) Несколько жителей собрались на митинг и заявили: «Вы все лжецы». Сколько рыцарей было?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
4. (2 балла) За круглым столом 6 жителей, каждый говорит: «Мой сосед справа — рыцарь». Сколько рыцарей?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
5. (2 балла) То же, но говорят: «Мой сосед слева — лжец». Сколько рыцарей?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
6. (3 балла) То же, но каждый говорит: «Оба мои соседа — лжецы». Сколько рыцарей?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}

Задание 3

Сиропчик угощает Пончика со Скатерти-самобранки: 6 пирожных и 6 конфет. Можно съесть только по 2 сразу. Если съесть:

• 2 пирожных или 2 конфеты — появляется 1 пирожное.
• 1 пирожное + 1 конфету — появляется 1 конфета.

(Скатерть обновляется перед каждым пунктом.)

1. (0.5 балла) Пончик съел 4 конфеты (2 пары). Сколько и чего теперь на скатерти?
   Ответ: \underline{\hspace{\linewidth}}
   
   
2. (1 балл) Сиропчик съел 4 пирожных (2 пары). Сколько и чего теперь на скатерти?
   Ответ: \underline{\hspace{\linewidth}}
   
   
3. (1.5 балла) Пончик съел 6 лакомств (парами). Могло ли остаться только конфеты?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
4. (2 балла) Сиропчик съел 8 лакомств (парами). Какое минимальное количество пирожных могло остаться?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
5. (2.5 балла) Сколько раз нужно есть парами, чтобы осталось ровно 1 лакомство?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}
   
   
6. (2.5 балла) Было 8 пирожных и 8 конфет. Осталось одно лакомство. Что это?
   Ответ: $\underline{\hspace{5cm}}$
   Обоснование: \underline{\hspace{\linewidth}}

Решения задач

1. [А)] Сколько маленьких кубиков имеют общую грань с чёрным кубиком?
   Решение: На рисунке чёрный кубик находится в углу объёмной фигуры, следовательно, он имеет три смежных кубика. Однако стандартные задачи часто подразумевают видимые соседние кубики на плоскости. Если предположить, что кубик расположен на поверхности конструкции, то общих граней будет 4 (левая, правая, передняя и верхняя/нижняя).
   Ответ: $\underline{4}$.
2. [Б)] Сколько всего получилось чёрных кубиков после первого взмаха?
   Решение: Первый взмах окрашивает все кубики, соприкасающиеся с исходным гранью. Исходный кубик имеет 4 смежных кубика. Изначально чёрный кубик 1. После первого взмаха: $1 + 4 = 5$.
   Ответ: $\underline{5}$.
3. [В)] Сколько всего получилось чёрных кубиков после второго взмаха?
   Решение: Второй взмах окрашивает кубики, соприкасающиеся с уже чёрными. Исходные 5 кубиков образуют крест. Каждый из четырёх новых кубиков добавляет по 3 новых соседа. Общее количество:
   $5 + 12 = 17$.
   Ответ: $\underline{17}$.
4. [Г)] Сколько всего получилось чёрных кубиков после третьего взмаха?
   Решение: Третий взмах добавляет следующий слой кубиков вокруг предыдущей фигуры. Общее количество чёрных кубиков образует куб $3 \times 3 \times 3$ с исключением угловых кубиков: $25$.
   Ответ: $\underline{25}$.
5. [Д)] Может ли такое быть, что башенки из 6 кубиков с разницей в 1 у соседних, сумма 63?
   Решение: Рассмотрим последовательность чисел: $8, 9, 10, 11, 12, 13$. Их сумма: $8 + 9 + 10 + 11 + 12 + 13 = 63$. Поэтому возможна ситуация, когда потеря одного кубика (из исходных 64) оставляет сумму 63.
   Ответ: $\underline{Да}$. Обоснование: Последовательность 8, 9, 10, 11, 12, 13 даёт сумму 63.
6. [Е)] Может ли Шпунтик построить 8 башенок из 63 кубиков с разностью 1 у соседних?
   Решение: Сумма восьми последовательных чисел вычисляется как $8a + 28 = 63$, что даёт нецелое $a = 4,375$. Чётное количество членов с разностью 1 не может дать нечётную сумму.
   Ответ: $\underline{Нет}$. Обоснование: Несуществует целочисленной последовательности с разностью 1 и суммой 63 для 8 элементов.

1. [А)] Человек говорит: «Я лжец». Является ли он жителем Острова?
   Решение: Рыцарь (всегда правдив) не может назвать себя лжецом. Лжец (всегда лжёт) тоже не может сказать «Я лжец» правдиво. Следовательно, утверждение приводит к парадоксу.
   Ответ: $\underline{Нет}$. Обоснование: Такое утверждение невозможно для рыцаря или лжеца.
2. [Б)] Два жителя сказали друг другу: «Ты лжец». Сколько среди них рыцарей?
   Решение: Если один рыцарь, то другой лжец (по его утверждению). И наоборот. Таким образом, среди двух жителей только один может быть рыцарем.
   Ответ: $\underline{1}$. Обоснование: Один рыцарь и один лжец — единственная возможная комбинация.
3. [В)] Сколько рыцарей было на митинге, где все сказали: «Вы все лжецы»?
   Решение: Если бы присутствовал хотя бы один рыцарь, его утверждение «Вы все лжецы» было бы ложью, что невозможно. Значит, все участники — лжецы, но их утверждение также ложно, что противоречиво.
   Ответ: $\underline{0}$. Обоснование: Невозможно одновременное наличие рыцарей и лжецов в такой ситуации.
4. [Г)] За круглым столом 6 жителей, каждый говорит: «Мой сосед справа — рыцарь». Сколько рыцарей?
   Решение: Если все рыцари, их утверждения истинны. Если все лжецы, их утверждения ложны. Однако цикл из шести человек требует одинаковых типов. Только вариант «все рыцари» непротиворечив.
   Ответ: $\underline{6}$. Обоснование: Все участники являются рыцарями, и их утверждения правдивы.
5. [Д)] То же, но говорят: «Мой сосед слева — лжец». Сколько рыцарей?
   Решение: Паттерн чередования Рыцарь-Лжец-Рыцарь-Лжец... образует цикл из трёх рыцарей и трёх лжецов.
   Ответ: $\underline{3}$. Обоснование: Каждый рыцарь указывает на лжеца слева, и наоборот.
6. [Е)] Каждый говорит: «Оба мои соседа — лжецы». Сколько рыцарей?
   Решение: Для истинности утверждения рыцаря его соседи должны быть лжецами. Лжецы, утверждая обратное, указывают, что хотя бы один сосед рыцарь. Чередование Рыцарь-Лжец-Рыцарь-Лжец... не работает для чётного круга. Решение: три рыцаря и три лжеца чередуются через одного.
   Ответ: $\underline{3}$. Обоснование: Каждый рыцарь окружён лжецами, лжецы указывают на наличие рыцарей.

1. [А)] Пончик съел 4 конфеты (2 пары). Сколько и чего теперь на скатерти?
   Решение: Каждая пара конфет добавляет 1 пирожное. Съедено 4 конфеты, добавлено 2 пирожных.
   Ответ: 8 пирожных и 2 конфеты.
2. [Б)] Сиропчик съел 4 пирожных (2 пары). Сколько и чего теперь на скатерти?
   Решение: Каждая пара пирожных уменьшает их количество на 1. Съедено 4 пирожных, осталось: $6 - (4 - 2) = 4$.
   Ответ: 4 пирожных и 6 конфет.
3. [В)] Могло ли остаться только конфеты после съедения 6 лакомств парами?
   Решение: Каждое парное съедение пирожных уменьшает их количество на 1. Удалить все пирожные невозможно, так как их итоговое количество должно быть нечётным.
   Ответ: $\underline{Нет}$. Обоснование: Нельзя полностью сократить пирожные до нуля.
4. [Г)] Какое минимальное количество пирожных могло остаться после съедения 8 лакомств?
   Решение: Минимизация достигается съедением смешанных пар (1 пирожное + 1 конфета), что уменьшает пирожные на 4.
   Ответ: 2 пирожных. Обоснование: Стратегия изменения парного выбора приводит к снижению количества пирожных.
5. [Д)] Сколько раз нужно есть парами, чтобы осталось ровно 1 лакомство?
   Решение: Каждое парное съедение уменьшает количество лакомств на 1. Начальное количество 12 → $\frac{12 - 1}{1} = 11$ действий.
   Ответ: $\underline{11}$. Обоснование: Общее количество лакомств уменьшается на 1 за каждое съедение.
6. [Е)] Что осталось: пирожное или конфета?
   Решение: Изначально оба количества чётны. Каждое действие меняет чётность только при добавлении. Итоговое единственное лакомство будет конфетой.
   Ответ: $\underline{Конфета}$. Обоснование: Чётность изменяется так, что конфета остаётся последней.