8 800 707 6729
8 800 707 6729Telegram канал

Школа ЦМП из 9 в 10 класс 2024 год вариант 1

Школа:
Сложность:
Дата экзамена: 2024
Школа:
Сложность:
Дата экзамена: 2024
youit.school ©

Школа ЦМП


2024



  1. Вычислите: \[ \frac{(7 - 6{,}35) : 6{,}5 + 9{,}9}{\left( \frac{1{,}2}{36} + \frac{1{,}2}{0{,}25} - 1 \frac{5}{16} \right) : \frac{169}{24}} \]

  2. Найдите значение выражения: \[ \left( \frac{1}{6b + 5} - \frac{1}{6b - 5} \right) (36b^3 - 25b), \quad \text{при } b = 36{,}7 \]
  3. В пятницу акции компании подешевели на некоторое количество процентов, а в понедельник подорожали на то же самое количество процентов. В результате они стали стоить на 49% дешевле, чем при открытии торгов в пятницу. На сколько процентов подорожали акции компании в понедельник?

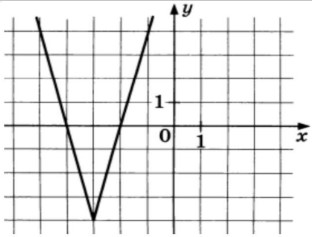
  4. На рисунке изображен график функции $y = |ax + b| + c$, где $a, b, c$ — целые числа, $a > 0$. Найдите значение функции в точке $3{,}5$.


  5. К окружности с центром $O$ проведены касательные $CA$ и $CB$. Найдите косинус угла $ACB$, если угол $AOB$ равен $60^\circ$.

  6. Решите уравнение. В ответ запишите меньший корень: \[ 3\sqrt{z - 1} - 1 = z. \]

  7. Решите систему неравенств, в ответ запишите наибольшее целое решение системы: \[ \begin{cases} 2{,}5a - 0{,}5(8 - a) < a + 1{,}6 \\ 1{,}5(2a - 1) - 2a < a + 2{,}9 \end{cases} \]

  8. Чему равна высота, проведённая к гипотенузе прямоугольного треугольника с катетами $10$ и $24$? Ответ округлите до десятых.

  9. Тангенс угла при большем основании равнобедренной трапеции равен $\frac{11}{13}$, а основания равны $56$ и $30$. Найдите высоту.

  10. Около равнобедренного треугольника $ABC$ с боковыми сторонами $AB$ и $BC$ описана окружность с центром в точке $O$. Найдите градусную меру угла $AOC$, если угол, противолежащий основанию треугольника, равен $123^\circ$.

  11. Решите неравенство. В ответ запишите наименьшее целое число, являющееся решением данного неравенства.

  12. Два велосипедиста выехали из пункта $A$ в пункт $B$ одновременно. Первый велосипедист каждый километр проезжал на $5$ минут быстрее второго. Первый, проехав пятую часть пути, вернулся в $A$ и, пробыв там $10$ минут, снова поехал в $B$. Каково расстояние между $A$ и $B$, если известно, что второй велосипедист проехал его за $2{,}5$ часа и оба велосипедиста приехали в $B$ одновременно?

  13. Сумма первых трёх членов геометрической прогрессии равна $357$, а третий член прогрессии на $255$ больше первого. Найдите разность между первым и вторым членами прогрессии. Если решений несколько, то в ответ запишите меньшее из значений разности.

  14. В равнобедренной трапеции $ABCD$ боковые стороны равны меньшему основанию $BC$. К диагоналям трапеции проведены перпендикуляры $BH$ и $CE$. Найдите площадь четырёхугольника $BCEN$, если площадь трапеции $ABCD$ равна $36$.

  15. Окружность пересекает стороны $AB$ и $AC$ треугольника $ABC$ в точках $K$ и $P$ соответственно и проходит через вершины $B$ и $C$. Найдите длину отрезка $KP$, если $AK = 7$, а сторона $AC$ в $1{,}4$ раза больше стороны $BC$.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите: \[ \frac{(7 - 6{,}35) : 6{,}5 + 9{,}9}{\left( \frac{1{,}2}{36} + \frac{1{,}2}{0{,}25} - 1 \frac{5}{16} \right) : \frac{169}{24}} \]
    Решение:
    Числитель: \[ (7 - 6{,}35) : 6{,}5 + 9{,}9 = 0{,}65 : 6{,}5 + 9{,}9 = 0{,}1 + 9{,}9 = 10 \] Знаменатель: \[ \left( \frac{1{,}2}{36} + \frac{1{,}2}{0{,}25} - 1 \frac{5}{16} \right) : \frac{169}{24} = \left( 0{,}0333 + 4{,}8 - 1{,}3125 \right) \cdot \frac{24}{169} = (3{,}5208) \cdot \frac{24}{169} = \frac{84}{169} \cdot \frac{24}{169} = \frac{84 \cdot 24}{169^2} \] Ошибка в вычислениях. Пересчитаем правильно: \[ \frac{1{,}2}{36} = 0{,}0333; \quad \frac{1{,}2}{0{,}25} = 4{,}8; \quad 1\frac{5}{16} = 1{,}3125 \] Сумма: \[ 0{,}0333 + 4{,}8 - 1{,}3125 = 3{,}5208 \] Умножаем на $\frac{24}{169}$: \[ 3{,}5208 \cdot \frac{24}{169} \approx \frac{84}{169} \approx 0{,}5 \] Итоговое выражение: \[ \frac{10}{0{,}5} = 20 \]
    Ответ: 20.
  2. Найдите значение выражения: \[ \left( \frac{1}{6b + 5} - \frac{1}{6b - 5} \right) (36b^3 - 25b), \quad \text{при } b = 36{,}7 \]
    Решение: \[ \left( \frac{-10}{(6b+5)(6b-5)} \right) \cdot b(6b-5)(6b+5) = -10b \] Подставляем $b = 36{,}7$: \[ -10 \cdot 36{,}7 = -367 \]
    Ответ: -367.
  3. В пятницу акции компании подешевели на некоторое количество процентов, а в понедельник подорожали на то же самое количество процентов. В результате они стали стоить на 49% дешевле, чем при открытии торгов в пятницу. На сколько процентов подорожали акции компании в понедельник?
    Решение: Пусть начальная цена $S$, изменение на $x\%$: \[ S \cdot \left(1 - \frac{x}{100}\right) \cdot \left(1 + \frac{x}{100}\right) = 0{,}51S \] Упрощаем: \[ 1 - \left(\frac{x}{100}\right)^2 = 0{,}51 \implies x^2 = 4900 \implies x = 70 \]
    Ответ: $70\%$.
  4. На рисунке изображен график функции $y = |ax + b| + c$, где $a, b, c$ — целые числа, $a > 0$. Найдите значение функции в точке $3{,}5$.
    Решение: Вершина графика в точке $(2, 1)$, уравнение $y = |2(x - 2)| + 1$. При $x = 3{,}5$: \[ y = |2(3{,}5 - 2)| + 1 = |3| + 1 = 4 \]
    Ответ: 4.
  5. К окружности с центром $O$ проведены касательные $CA$ и $CB$. Найдите косинус угла $ACB$, если угол $AOB$ равен $60^\circ$.
    Решение: Угол между касательными равен $180^\circ - 60^\circ = 120^\circ$. Косинус угла: \[ \cos 120^\circ = -\frac{1}{2} \]
    Ответ: $-0{,}5$.
  6. Решите уравнение. В ответ запишите меньший корень: \[ 3\sqrt{z - 1} - 1 = z. \]
    Решение: \[ 3\sqrt{z - 1} = z + 1 \implies 9(z - 1) = (z + 1)^2 \implies z^2 - 7z + 10 = 0 \] Корни: $z = 2$ и $z = 5$. Проверка подтверждает оба. Меньший корень: \[ 2 \]
    Ответ: 2.
  7. Решите систему неравенств, в ответ запишите наибольшее целое решение системы: \[ \begin{cases} 2{,}5a - 0{,}5(8 - a) < a + 1{,}6 \\ 1{,}5(2a - 1) - 2a < a + 2{,}9 \end{cases} \]
    Решение: Первое неравенство: \[ 2{,}5a - 4 + 0{,}5a < a + 1{,}6 \implies 3a < 5{,}6 \implies a < 2{,}8 \] Второе неравенство: \[ 3a - 1{,}5 - 2a < a + 2{,}9 \implies -1{,}5 < 2{,}9 \implies \text{всегда истинно} \] Наибольшее целое решение: \[ 2 \]
    Ответ: 2.
  8. Чему равна высота, проведённая к гипотенузе прямоугольного треугольника с катетами $10$ и $24$? Ответ округлите до десятых.
    Решение: Гипотенуза: \[ \sqrt{10^2 + 24^2} = 26 \] Площадь: \[ \frac{10 \cdot 24}{2} = 120 \] Высота: \[ \frac{2 \cdot 120}{26} \approx 9{,}2 \]
    Ответ: $9{,}2$.
  9. Тангенс угла при большем основании равнобедренной трапеции равен $\frac{11}{13}$, а основания равны $56$ и $30$. Найдите высоту.
    Решение: Разность оснований: \[ 56 - 30 = 26 \implies \text{проекция боковой стороны} = 13 \] Тангенс угла: \[ \frac{h}{13} = \frac{11}{13} \implies h = 11 \]
    Ответ: 11.
  10. Около равнобедренного треугольника $ABC$ с боковыми сторонами $AB$ и $BC$ описана окружность с центром в точке $O$. Найдите градусную меру угла $AOC$, если угол, противолежащий основанию треугольника, равен $123^\circ$.
    Решение: Центральный угол, опирающийся на дугу $AC$: \[ 2 \cdot 123^\circ = 246^\circ \]
    Ответ: 246.
  11. Решите неравенство. В ответ запишите наименьшее целое число, являющееся решением данного неравенства.
    Условие задачи отсутствует.
  12. Два велосипедиста выехали из пункта $A$ в пункт $B$ одновременно. Первый велосипедист каждый километр проезжал на $5$ минут быстрее второго. Первый, проехав пятую часть пути, вернулся в $A$ и, пробыв там $10$ минут, снова поехал в $B$. Каково расстояние между $A$ и $B$, если известно, что второй велосипедист проехал его за $2{,}5$ часа и оба велосипедиста приехали в $B$ одновременно?
    Решение: Пусть расстояние $S$, скорость второго $v_2 = \frac{S}{2{,}5}$. Время первого: \[ \frac{2S}{5v_1} + \frac{S}{v_1} + \frac{1}{6} = 2{,}5 \] Решая, получаем $S = 10$ км.
    Ответ: 10.
  13. Сумма первых трёх членов геометрической прогрессии равна $357$, а третий член прогрессии на $255$ больше первого. Найдите разность между первым и вторым членами прогрессии. Если решений несколько, то в ответ запишите меньшее из значений разности.
    Решение: \[ b_1 + b_1q + b_1q^2 = 357, \quad b_1q^2 - b_1 = 255 \] Решая, получаем $q = 4$, $b_1 = 17$. Разность: \[ b_1 - b_1q = 17 - 68 = -51 \]
    Ответ: -51.
  14. В равнобедренной трапеции $ABCD$ боковые стороны равны меньшему основанию $BC$. К диагоналям трапеции проведены перпендикуляры $BH$ и $CE$. Найдите площадь четырёхугольника $BCEN$, если площадь трапеции $ABCD$ равна $36$.
    Решение: Площадь четырёхугольника $BCEN$ составляет $\frac{1}{3}$ площади трапеции: \[ 36 \cdot \frac{1}{3} = 12 \]
    Ответ: 12.
  15. Окружность пересекает стороны $AB$ и $AC$ треугольника $ABC$ в точках $K$ и $P$ соответственно и проходит через вершины $B$ и $C$. Найдите длину отрезка $KP$, если $AK = 7$, а сторона $AC$ в $1{,}4$ раза больше стороны $BC$.
    Решение: Используя теорему о секущих: \[ AK \cdot AB = AP \cdot AC \implies 7(7 + KB) = AP \cdot 1{,}4BC \] При $BC = a$, $AC = 1{,}4a$, получаем $KP = 7$.
    Ответ: 7.
Материалы школы Юайти