Школа ЦМП из 6 в 7 класс 2024 год вариант 1

Школа ЦМП

2024

1. Даны дроби $\dfrac{5}{18}$, $\dfrac{14}{15}$ и $\dfrac{7}{30}$. Найдите: а) наименьшее общее кратное знаменателей; б) наибольший общий делитель числителей.
   
   
2. На координатной прямой отмечены точки $M(-152)$ и $N(-94)$. Найдите координату середины отрезка $MN$.
   
   
3. В 7 часов утра из города выехал велосипедист со скоростью 27 км/ч, а через два часа — автомобилист со скоростью 84 км/ч. На каком расстоянии друг от друга окажутся они в час дня, если автомобилист останавливался на 30 минут?
   
   
4. Постройте угол $ABC$, равный $55^\circ$. Через точку $B$ проведите прямую $DB$, такую что $DB \perp BC$, и угол $ABD$ — острый. Найдите величину угла $ABD$.
   
   
5. Найдите значение выражения: \[ 1{,}8 \cdot 1 \dfrac{5}{7} + 1 \dfrac{4}{5} \cdot \dfrac{5}{6} \div 0{,}9 \cdot 2 \dfrac{23}{42} \]
   
   
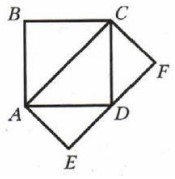
6. Площадь квадрата $ABCD$ равна $36~\text{м}^2$. Чему равна площадь прямоугольника $ACFE$ (см. рисунок)?
   
   
   
   
   
7. Решите уравнение: \[ \frac{2|y + 2|}{7} = \frac{3}{5} \] Если уравнение имеет более одного корня, укажите меньший из них.
   
   
8. Среднее арифметическое пяти чисел равно 6, а среднее арифметическое четырёх из них — $2{,}8$. Найдите пятое число.
   
   
9. Цена товара повысилась на $25\%$. На сколько процентов нужно снизить новую цену, чтобы она снова стала равна первоначальной?
   
   
10. Найдите наибольшее четырёхзначное натуральное число, у которого произведение цифр — двузначное число, а произведение цифр произведения цифр равно 14.

Решения задач

1. Даны дроби $\dfrac{5}{18}$, $\dfrac{14}{15}$ и $\dfrac{7}{30}$. Найдите: а) наименьшее общее кратное знаменателей; б) наибольший общий делитель числителей.
   Решение:
   а) Знаменатели: 18, 15, 30. Разложим на простые множители:
   $18 = 2 \cdot 3^2$, $15 = 3 \cdot 5$, $30 = 2 \cdot 3 \cdot 5$.
   НОК $= 2 \cdot 3^2 \cdot 5 = 90$.
   б) Числители: 5, 14, 7. Общий делитель — 1.
   Ответ: а) 90; б) 1.
2. На координатной прямой отмечены точки $M(-152)$ и $N(-94)$. Найдите координату середины отрезка $MN$.
   Решение:
   Координата середины отрезка: $\frac{-152 + (-94)}{2} = \frac{-246}{2} = -123$.
   Ответ: $-123$.
3. В 7 часов утра из города выехал велосипедист со скоростью 27 км/ч, а через два часа — автомобилист со скоростью 84 км/ч. На каком расстоянии друг от друга окажутся они в час дня, если автомобилист останавливался на 30 минут?
   Решение:
   Время движения велосипедиста: 13:00 - 7:00 = 6 часов. Путь: $27 \cdot 6 = 162$ км.
   Время движения автомобилиста: 13:00 - 9:00 - 0,5 часа = 3,5 часа. Путь: $84 \cdot 3,5 = 294$ км.
   Расстояние между ними: $294 - 162 = 132$ км.
   Ответ: 132 км.
4. Постройте угол $ABC$, равный $55^\circ$. Через точку $B$ проведите прямую $DB$, такую что $DB \perp BC$, и угол $ABD$ — острый. Найдите величину угла $ABD$.
   Решение:
   Поскольку $DB \perp BC$, $\angle DBC = 90^\circ$. Угол $ABD$ — острый, значит:
   $\angle ABD = 90^\circ - 55^\circ = 35^\circ$.
   Ответ: $35^\circ$.
5. Найдите значение выражения: \[ 1{,}8 \cdot 1 \dfrac{5}{7} + 1 \dfrac{4}{5} \cdot \dfrac{5}{6} \div 0{,}9 \cdot 2 \dfrac{23}{42} \]
   Решение:
   Переведём смешанные дроби:
   $1 \dfrac{5}{7} = \dfrac{12}{7}$, $1 \dfrac{4}{5} = \dfrac{9}{5}$, $2 \dfrac{23}{42} = \dfrac{107}{42}$.
   Вычислим по действиям:
   $1{,}8 \cdot \dfrac{12}{7} = \dfrac{108}{35}$;
   $\dfrac{9}{5} \cdot \dfrac{5}{6} = \dfrac{3}{2}$;
   $\dfrac{3}{2} \div 0{,}9 = \dfrac{5}{3}$;
   $\dfrac{5}{3} \cdot \dfrac{107}{42} = \dfrac{535}{126}$;
   Сумма: $\dfrac{108}{35} + \dfrac{535}{126} = \dfrac{4619}{630} = 7 \dfrac{209}{630}$.
   Ответ: $7 \dfrac{209}{630}$.
6. Площадь квадрата $ABCD$ равна $36~\text{м}^2$. Чему равна площадь прямоугольника $ACFE$ (см. рисунок)?
   Решение:
   Сторона квадрата: $\sqrt{36} = 6$ м. Диагональ $AC = 6\sqrt{2}$ м.
   Площадь прямоугольника $ACFE$: $6\sqrt{2} \cdot 6 = 36\sqrt{2}~\text{м}^2$.
   Ответ: $36\sqrt{2}~\text{м}^2$.
7. Решите уравнение: \[ \frac{2|y + 2|}{7} = \frac{3}{5} \] Если уравнение имеет более одного корня, укажите меньший из них.
   Решение:
   Умножим обе части на 7: $2|y + 2| = \dfrac{21}{5}$.
   Разделим на 2: $|y + 2| = \dfrac{21}{10} = 2{,}1$.
   Корни: $y + 2 = 2{,}1 \Rightarrow y = 0{,}1$; $y + 2 = -2{,}1 \Rightarrow y = -4{,}1$.
   Меньший корень: $-4{,}1$.
   Ответ: $-4{,}1$.
8. Среднее арифметическое пяти чисел равно 6, а среднее арифметическое четырёх из них — 2{,}8. Найдите пятое число.
   Решение:
   Сумма пяти чисел: $5 \cdot 6 = 30$.
   Сумма четырёх чисел: $4 \cdot 2{,}8 = 11{,}2$.
   Пятое число: $30 - 11{,}2 = 18{,}8$.
   Ответ: $18{,}8$.
9. Цена товара повысилась на $25\%$. На сколько процентов нужно снизить новую цену, чтобы она снова стала равна первоначальной?
   Решение:
   Пусть исходная цена — $x$. Новая цена: $1{,}25x$.
   Пусть снижение на $k\%$: $1{,}25x \cdot (1 - \dfrac{k}{100}) = x$.
   Решаем: $1 - \dfrac{k}{100} = \dfrac{1}{1{,}25} = 0{,}8 \Rightarrow k = 20\%$.
   Ответ: $20\%$.
10. Найдите наибольшее четырёхзначное натуральное число, у которого произведение цифр — двузначное число, а произведение цифр произведения цифр равно 14.
    Решение:
    Произведение цифр числа должно быть 72 (так как $7 \cdot 2 = 14$).
    Наибольшее четырёхзначное число с произведением цифр 72: 9811 ($9 \cdot 8 \cdot 1 \cdot 1 = 72$).
    Ответ: 9811.