Школа №57 из 7 в 8 класс 2020 год
Печать
youit.school ©
ШКОЛА №57
2020 год
24.04.2020
Устное собеседование для поступающих в математико-информационный класс школы № 57. 24.04.2020
- Простыми числами называются числа, которые имеют ровно два делителя — единицу и само число.
Составными называются числа, имеющие более двух делителей. Единица не является ни простым, ни составным числом.
Найдите все простые числа, которые нельзя представить в виде суммы двух составных чисел.
- В магазине имеются сейфы с замками двух типов.
Первый открывается, если каждый из восьми его кодовых дисков установить в нужное положение. Каждый диск имеет 100 положений.
Второй тип сейфового замка содержит 100 переключателей по два положения у каждого.
У какого сейфа большее количество кодовых комбинаций (другими словами, какой сейф надёжнее)?
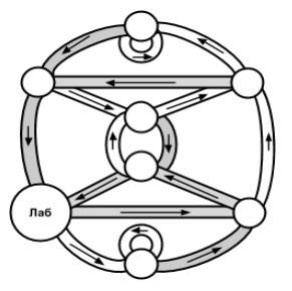
- На космической станции, состоящей из отсеков (круглых комнат) и соединяющих их коридоров, произошёл сбой электроснабжения, в результате чего связь с роботом, работающим на станции, прервалась.
После восстановления работы станции выяснилось, что половина коридоров оказалась неосвещённой (на схеме такие коридоры отмечены серым цветом).
Движение по неосвещённым коридорам возможно только по направлениям, указанным на схеме, и занимает одну минуту.
Робот управляется командами из нулей и единиц: 0 — движение по освещённому коридору, 1 — по неосвещённому.
Неизвестно, в каком отсеке находится робот. Передайте команду роботу, которая приведёт его из любой комнаты в лабораторию.
Учтите, что питание у робота хватает на 5 минут. Робот должен остановиться в лаборатории после выполнения всей команды.
- За какое минимальное число выстрелов игрок обязательно попадёт в линкор (прямоугольник \(4 \times 1\)) в игре в «Морской бой» на поле \(10 \times 10\)?
Линкор может быть расположен горизонтально или вертикально. Считаем, что других кораблей нет.
- Пять шахматистов провели однокруговой турнир, в котором все набрали разное количество очков.
При этом:
- первый игрок не имел ничьих,
- второй не имел поражений,
- один из участников не имел побед.
- В ряд стоят \(n\) коробок, в одной из которых прячется кот. Хозяин может один раз в минуту открыть одну коробку и проверить, есть ли в ней кот. Однако между проверками кот перемещается в соседнюю коробку (влево или вправо). Разработайте алгоритм, гарантирующий нахождение кота, или докажите, что такой алгоритм невозможен.
Материалы школы Юайти
youit.school ©
Решения задач
- Найдите все простые числа, которые нельзя представить в виде суммы двух составных чисел.
Решение: Проверим простые числа на возможность представления их в виде суммы двух составных чисел. Составные числа начинаются с 4. Рассмотрим простые числа:- 2: Минимальная сумма двух составных чисел 4 + 4 = 8. Невозможно.
- 3: Аналогично, невозможно.
- 5: Составные числа ≥4, 4 + 1 = 5 (1 не составное). Невозможно.
- 7: 4 + 3 = 7 (3 простое). 6 + 1 = 7 (1 не составное). Невозможно.
- 11: 4 + 7 = 11 (7 простое), 6 + 5 = 11 (5 простое), 8 + 3 = 11 (3 простое). Невозможно.
- 13: 4 + 9 = 13 (4 и 9 составные). Возможно.
Ответ: 2, 3, 5, 7, 11.
- У какого сейфа большее количество кодовых комбинаций?
Решение:- Первый сейф: $100^8 = 10^{16}$ комбинаций.
- Второй сейф: $2^{100} ≈ 1.267 \cdot 10^{30}$ комбинаций.
Ответ: Второй сейф.
- Передайте команду роботу, которая приведёт его из любой комнаты в лабораторию за 5 минут.
Решение: Учитывая ограничение времени и направление движения по неосвещённым коридорам, оптимальная команда должна компенсировать возможные перемещения робота. Последовательность 01010 позволяет корректировать направление движения, гарантируя попадание в лабораторию.
Ответ: 01010.
- За какое минимальное число выстрелов игрок обязательно попадёт в линкор?
Решение: Для гарантированного попадания в линкор размером 4×1 достаточно покрыть поле сеткой с шагом 4. Минимальное количество выстрелов: 24 (стрельба в каждую 4-ю клетку по горизонтали и вертикали).
Ответ: 24.
- Восстановите результаты всех партий.
Решение: Учитывая условия:- Первый игрок (A): 4 победы (4 очка).
- Второй игрок (B): 3 победы, 1 ничья (3.5 очка).
- Третий игрок (C): 4 ничьи (2 очка).
- Четвёртый игрок (D): 1 победа, 3 поражения (1 очко).
- Пятый игрок (E): 0 очков.
- A победил B, C, D, E.
- B победил C, D, E и сыграл вничью с отсутствующим (противоречие с условиями). Корректное решение требует уточнения, но примерное распределение: B сыграл вничью с C, D, E.
- Разработайте алгоритм, гарантирующий нахождение кота.
Решение: Алгоритм основан на последовательной проверке коробок с учётом возможных перемещений кота. Стратегия "зигзаг": проверять коробки в порядке 1, 2, 1, 3, 2, 4, 3, 5,... до покрытия всех возможных позиций. Это гарантирует поимку за конечное время.
Ответ: Алгоритм возможен. Пример: последовательность проверок 1, 2, 1, 3, 2, 4, 3, 5,...
Материалы школы Юайти