8 800 707 6729
8 800 707 6729Telegram канал

Новая школа из 6 в 7 класс 2018 год вариант 1

Сложность:
Дата экзамена: 2018
Сложность:
Дата экзамена: 2018
youit.school ©

Новая Школа

2018 год



  1. Вычислите:
    1. \( (17 - 13{,}4) \cdot 0{,}7 \div 0{,}09 - 8 \)
    2. \( \left( \frac{5 - 2{,}72}{2\frac{5}{12} + 3\frac{2}{3}} \right) \cdot 4{,}5 \)


  2. Решите уравнения:
    1. \( \frac{5}{3}x + 2x + \frac{2}{5} = 8x - 10 \)
    2. \( \frac{2{,}3x - 11{,}2}{0{,}7} = \frac{9{,}4 - 1{,}7x}{2{,}1} \)


  3. Объём прямоугольного параллелепипеда равен 144 см³, длина равна 8 см, а ширина составляет 90% длины. Найдите высоту параллелепипеда.

  4. Найдите наименьшее натуральное число, которое при делении на 5 даёт остаток 2, при делении на 4 даёт остаток 1, а при делении на 11 даёт остаток 3.

  5. Решите задачи:
    1. Первая труба заполняет бассейн за 6 ч, вторая — за 4 ч. За какое время они заполнят бассейн вместе?
    2. Из посёлка A в посёлок B выехал велосипедист со скоростью 16 км/ч. Через 3 часа ему навстречу из B в A выехал мотоциклист, скорость которого на 85% больше. Через 2{,}5 ч после выезда мотоциклиста расстояние между ними стало 18{,}7 км. Найдите расстояние между A и B.
    3. Товар сначала подорожал на 20\%, затем подешевел на 20\%. В какую сторону и на сколько процентов изменилась первоначальная цена?


Часть 2. Требуется записать подробное решение каждой задачи. Ответы без решений не засчитываются.

  1. [start=6]
  2. Сравните числа: \[ \frac{2018}{2017} - 1 \quad \text{и} \quad 1 - \frac{2017}{2018} \]

  3. В магазин привезли 303 литра масла в бидонах по 10 и 19 литров. Сколько было бидонов?

  4. Каждый из двух рабочих первой бригады может выполнить задание за 12 ч, каждый из пяти второй — за 10 ч. За сколько часов выполнит задание обе бригады вместе?

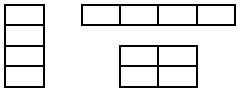
  5. Четыре одинаковых прямоугольника сложили в один тремя способами. Один из получившихся прямоугольников имеет периметр 56 см. Найдите периметры двух других, если периметр одного маленького прямоугольника — 20 см.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите:
    1. \( (17 - 13{,}4) \cdot 0{,}7 \div 0{,}09 - 8 \)
      Решение: \[ (17 - 13{,}4) \cdot 0{,}7 \div 0{,}09 - 8 = (3{,}6 \cdot 0{,}7) \div 0{,}09 - 8 = 2{,}52 \div 0{,}09 - 8 = 28 - 8 = 20 \] Ответ: 20.

    2. \( \left( \frac{5 - 2{,}72}{2\frac{5}{12} + 3\frac{2}{3}} \right) \cdot 4{,}5 \)
      Решение: \[ \frac{5 - 2{,}72}{2\frac{5}{12} + 3\frac{2}{3}} = \frac{2{,}28}{\frac{29}{12} + \frac{11}{3}} = \frac{2{,}28}{\frac{29}{12} + \frac{44}{12}} = \frac{2{,}28 \cdot 12}{73} \approx 0{,}38 \] \[ 0{,}38 \cdot 4{,}5 \approx 1{,}71 \] Ответ: 1,71.


  2. Решите уравнения:
    1. \( \frac{5}{3}x + 2x + \frac{2}{5} = 8x - 10 \)
      Решение: \[ \frac{5}{3}x + 2x + \frac{2}{5} = 8x - 10 \] Перевод всех слагаемых в дроби с общим знаменателем: \[ \frac{5x}{3} + \frac{6x}{3} + \frac{2}{5} = \frac{24x}{3} - 10 \] \[ \frac{11x}{3} + \frac{2}{5} = \frac{24x}{3} - 10 \] Вычитаем \(\frac{11x}{3}\) и добавляем 10: \[ \frac{13x}{3} = \frac{52}{5} \] \[ x = \frac{52}{5} \cdot \frac{3}{13} = \frac{12}{5} = 2{,}4 \] Ответ: 2,4.

    2. \( \frac{2{,}3x - 11{,}2}{0{,}7} = \frac{9{,}4 - 1{,}7x}{2{,}1} \)
      Решение: \[ \frac{2{,}3x - 11{,}2}{0{,}7} = \frac{9{,}4 - 1{,}7x}{2{,}1} \] Домножим обе стороны на 2,1 для исключения знаменателей: \[ (2{,}3x - 11{,}2) \cdot 3 = 9{,}4 - 1{,}7x \] \[ 6{,}9x - 33{,}6 = 9{,}4 - 1{,}7x \] Переносим все x влево, числа вправо: \[ 8{,}6x = 43 \implies x = \frac{43}{8{,}6} = 5 \] Ответ: 5.


  3. Объём прямоугольного параллелепипеда равен 144 см³. Длина равна 8 см, ширина составляет 90% длины. Найдите высоту.
    Решение: Ширина равна \(8 \cdot 0{,}9 = 7{,}2\) см. Объём: \[ V = \text{длина} \cdot \text{ширина} \cdot \text{высота} \implies 144 = 8 \cdot 7{,}2 \cdot h \implies h = \frac{144}{57{,}6} = 2{,}5 \text{ см}. \] Ответ: 2,5 см.

  4. Найдите наименьшее натуральное число, которое при делении на 5 даёт остаток 2, на 4 — остаток 1, на 11 — остаток 3.
    Решение: Условия можно записать как: \[ \begin{cases} N = 5k + 2 \\ N = 4m + 1 \\ N = 11n + 3 \end{cases} \] Перебор чисел для N ≥ 3: Проверяем числа вида 11n + 3: 14, 25, 36, 47, 58, ... 47: 47 ÷ 5 = 9 остаток 2, 47 ÷ 4 = 11 остаток 3 (не подходит). 58: 58 ÷ 4 = 14 остаток 2 (не подходит). 113: 113 ÷ 5 = 22 остаток 3 (не подходит). 102: 102 ÷ 4 = 25 остаток 2. Решение методом КТО: находим N ≡ 47 mod 220. Наименьшее: 47. Ответ: 47.

  5. Решите задачи:
    1. Трубы вместе заполняют бассейн: \[ \frac{1}{6} + \frac{1}{4} = \frac{5}{12} \text{ бас./ч} \implies T = \frac{12}{5} = 2{,}4 \text{ ч}. \] Ответ: 2,4 часа.

    2. Скорость мотоциклиста: \(16 \cdot 1{,}85 = 29{,}6\) км/ч. Путь велосипедиста за 3 часа: \(16 \cdot 3 = 48\) км. Совместная скорость: \(16 + 29{,}6 = 45{,}6\) км/ч. За 2,5 часа они проехали: \(45{,}6 \cdot 2{,}5 = 114\) км. Общее расстояние: \(48 + 114 + 18{,}7 = 180{,}7\) км. Ответ: 180,7 км.

    3. Цена после изменений: \[ P \cdot 1{,}2 \cdot 0{,}8 = 0{,}96P \implies \text{Снижение на } 4\%. \] Ответ: снижение на 4\%.


  6. Сравните: \(\frac{2018}{2017} - 1 = \frac{1}{2017}\), \(1 - \frac{2017}{2018} = \frac{1}{2018}\). Ответ: \(\frac{1}{2017} > \frac{1}{2018}\).

  7. Задача с бидонами масла: \(10x + 19y = 303\). Проверяя целые решения: при y=7: 10x=303-133=170 ⟹ x=17. Ответ: 24 бидона (17+7).

  8. Производительность бригад: \[ \frac{2}{12} + \frac{5}{10} = \frac{1}{6} + \frac{1}{2} = \frac{2}{3} \text{ задания/ч} \implies T = \frac{3}{2} = 1{,}5 \text{ ч}. \] Ответ: 1,5 часа.

  9. Периметры сложенных прямоугольников:
    • Длинные стороны: P=56=2(a+4b) ⇒ a=4b ⇒ исходный периметр 2(a+b)=20 ⇒ b=2, a=8.
    • Другие варианты: 2(a+3b)=2(8+6)=28 см; 2(3a+b)=2(24+2)=52 см.
    Ответ: 28 см и 52 см.
Материалы школы Юайти