8 800 707 6729
8 800 707 6729Telegram канал

Новая школа из 5 в 6 класс 2018 год вариант 1

Сложность:
Дата экзамена: 2018
Сложность:
Дата экзамена: 2018
youit.school ©

Новая Школа

2018 год



  1. Вычислите, в ответ запишите результат:
    1. \(53 \cdot 182\)
    2. \(6539 \div 13\)
    3. \(5{,}71 + 32{,}9 - 0{,}187\)
    4. \(\frac{5}{7} + \frac{6}{7}\)
    5. \(\frac{100}{111} - \frac{13}{111}\)
    6. \(135 - 75 \div (359 - 344) + 8 \cdot 17\)


  2. Решите уравнения, запишите корень:
    1. \(6 \cdot 15 + \frac{4200}{6x - 10} = 300\)
    2. \(4(2x + 2{,}1) - 4 = 12{,}4\)
    3. \((x + 6)x + x(4 - x) = 2(3x + (9 - x))\)


  3. У Пети было несколько яблок, он сорвал ещё 21 яблоко. Затем он поделил все яблоки на четыре равные части и забрал себе одну. В результате у Пети стало столько же яблок, сколько было в начале. Сколько яблок у Пети?

  4. На экзамен в Новую школу пришли 94 ученика. Их рассадили в три помещения. В первом писало экзамен в 4 раза меньше, чем в третьем, а в третьем — на 5 человек больше, чем во втором. Сколько человек было в каждом помещении?

  5. Обведите правильный ответ: Ширину прямоугольника уменьшили на \(a\) см. На сколько сантиметров уменьшится его периметр?
    • \(a\)
    • \(a \cdot 2\)
    • \(a \div 2\)
    • не хватает данных


  6. Сравните дроби (поставьте знак между числами):
    1. \(\frac{65}{76} \ \rule{1cm}{0.4pt} \ \frac{56}{76}\)
    2. \(\frac{18}{17} \ \rule{1cm}{0.4pt} \ \frac{13}{18}\)
    3. \(\frac{18}{21} \ \rule{1cm}{0.4pt} \ \frac{15}{18}\)


Часть 2. Запишите подробное решение. Ответы без решения не засчитываются.

  1. [start=7]
  2. Среди дробей \(\frac{a}{7}, \frac{7}{a}, \frac{a}{a}\) выберите наименьшую, если \(a > 7\). Объясните свой выбор.

  3. Спички складывают в виде квадратов:
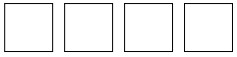
    1. Сколько нужно спичек, чтобы выложить 80 таких квадратов?
    2. Сколько квадратов можно выложить из 80 спичек?


  4. Теперь спички выкладываются иначе (рядом общими сторонами):
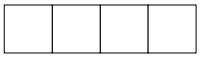
    1. Сколько нужно спичек, чтобы выложить 70 таких квадратов?
    2. Сколько квадратов можно выложить из 70 спичек?


  5. Гриша узнал, что для выкладки 50 одинаковых элементов нужно 251 спичка. Его расчёт: \(1 + 5 \cdot 50 = 251\) Найди, как устроены эти узоры. Объясни ответ.


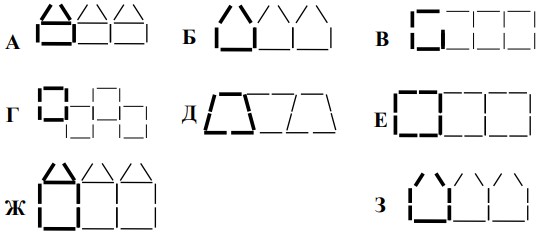
  6. Ученик-кондитер работал 2 часа. Потом к нему присоединился мастер, который делает на 40 плюшек в час больше. Через 5 часов мастер обогнал ученика на 120 плюшек. Сколько плюшек в час делает ученик?
Материалы школы Юайти
youit.school ©

Решения задач



    1. Вычислить: \(53 \cdot 182\)
      Решение:
      \(53 \cdot 182 = 53 \cdot (180 + 2) = 53 \cdot 180 + 53 \cdot 2 = 9540 + 106 = 9646\)
      Ответ: \(9646\).

    2. Вычислить: \(6539 \div 13\)
      Решение:
      \(6539 \div 13 = 503\) (проверка: \(13 \cdot 503 = 6539\))
      Ответ: \(503\).

    3. Вычислить: \(5{,}71 + 32{,}9 - 0{,}187\)
      Решение:
      \(5{,}71 + 32{,}9 = 38{,}61\); \(38{,}61 - 0{,}187 = 38{,}423\)
      Ответ: \(38{,}423\).

    4. Вычислить: \(\frac{5}{7} + \frac{6}{7}\)
      Решение:
      \(\frac{5}{7} + \frac{6}{7} = \frac{11}{7} = 1 \frac{4}{7}\)
      Ответ: \(\frac{11}{7}\) или \(1 \frac{4}{7}\).

    5. Вычислить: \(\frac{100}{111} - \frac{13}{111}\)
      Решение:
      \(\frac{100}{111} - \frac{13}{111} = \frac{87}{111} = \frac{29}{37}\) (после сокращения)
      Ответ: \(\frac{29}{37}\).

    6. Вычислить: \(135 - 75 \div (359 - 344) + 8 \cdot 17\)
      Решение:
      \(359 - 344 = 15\); \(75 \div 15 = 5\); \(8 \cdot 17 = 136\)
      \(135 - 5 + 136 = 266\)
      Ответ: \(266\).


    1. Решить уравнение: \(6 \cdot 15 + \frac{4200}{6x - 10} = 300\)
      Решение:
      \(90 + \frac{4200}{6x - 10} = 300\) \(\frac{4200}{6x - 10} = 210\) \(6x - 10 = 20\) \(6x = 30\) \(x = 5\) Ответ: \(5\).

    2. Решить уравнение: \(4(2x + 2{,}1) - 4 = 12{,}4\)
      Решение:
      \(8x + 8{,}4 - 4 = 12{,}4\) \(8x + 4{,}4 = 12{,}4\) \(8x = 8\) \(x = 1\) Ответ: \(1\).

    3. Решить уравнение: \((x + 6)x + x(4 - x) = 2(3x + (9 - x))\)
      Решение:
      \(x^2 + 6x + 4x - x^2 = 2(2x + 9)\) \(10x = 4x + 18\) \(6x = 18\) \(x = 3\) Ответ: \(3\).


  3. У Пети было несколько яблок.
    Решение:
    Пусть у Пети было \(x\) яблок. После сбора: \(x + 21\). После деления на 4 части: \(\frac{x + 21}{4}\). Уравнение:
    \(\frac{x + 21}{4} = x\) \(x + 21 = 4x\) \(3x = 21\) \(x = 7\) Ответ: \(7\).
  4. Распределение учеников на экзамене.
    Решение:
    Пусть во втором помещении \(y\) человек, тогда в третьем \(y + 5\), в первом \(\frac{y + 5}{4}\). Общее уравнение:
    \(\frac{y + 5}{4} + y + y + 5 = 94\) \(\frac{9y + 25}{4} = 94\) \(9y + 25 = 376\) \(9y = 351\) \(y = 39\) Второе помещение: \(39\), третье: \(44\), первое: \(11\). Ответ: \(11\), \(39\), \(44\).
  5. Выбор ответа: уменьшение периметра. Ответ: Периметр уменьшится на \(2a\), вариант \(2)\).
    1. \(\frac{65}{76} > \frac{56}{76}\) (одинаковые знаменатели).
    2. \(\frac{18}{17} > \frac{13}{18}\) (\(\frac{18}{17} > 1\), \(\frac{13}{18} < 1\)).
    3. \(\frac{18}{21} = \frac{6}{7} \approx 0{,}857\); \(\frac{15}{18} = \frac{5}{6} \approx 0{,}833\) \(\Rightarrow\) \(\frac{18}{21} > \frac{15}{18}\).
  7. Наименьшая дробь при \(a > 7\): \(\frac{7}{a} < \frac{a}{a} = 1 < \frac{a}{7}\). Ответ: \(\frac{7}{a}\).
    1. Спички для 80 квадратов (цепочка): Формула \(4 + 3(n - 1)\), для \(n=80\): \(4 + 3 \cdot 79 = 241\). Ответ: \(241\).
    2. Квадратов из 80 спичек: \(3n + 1 \leq 80\) \(\Rightarrow n \leq \frac{79}{3} \approx 26\). Ответ: \(26\).
    1. Спички для 70 квадратов: Формула аналогично задаче 8: \(4 + 3 \cdot 69 = 211\). Ответ: \(211\).
    2. Квадратов из 70 спичек: \(3n + 1 \leq 70\) \(\Rightarrow n \leq 23\). Ответ: \(23\).
  10. Узор из элементов: Первый элемент требует 1 спичку, каждый следующий добавляет 5. Ответ: элементы соединены последовательно, первый уникальный, остальные требуют 5 спичек каждый (пример: звезда).
  11. Производительность ученика. Решение:
    Пусть ученик делает \(x\) плюшек в час. Тогда: Ученик за 7 часов: \(7x\), мастер за 5 часов: \(5(x + 40)\). Уравнение: \(5(x + 40) - 7x = 120\) \(5x + 200 - 7x = 120\) \(-2x = -80\) \(x = 40\) Ответ: \(40\) плюшек в час.
Материалы школы Юайти