8 800 707 6729
8 800 707 6729Telegram канал

Могилёвский Лицей №1 из 9 в 10 класс 2016 год вариант 2

Сложность:
Дата экзамена: 2016
Печать
youit.school ©

МОГИЛЁВСКИЙ ЛИЦЕЙ №1


2016 год


Вариант 2



  1. Известно, что \[ a^3 > a^4. \] Тогда число \(a\) может быть равно \[ -3,\;-\tfrac{1}{3},\;3,\;\sqrt{3},\;\tfrac{1}{3}. \]
  2. На какой угол повернётся минутная стрелка за 5 минут?

  3. Найдите величину угла \(x\), если \(O\) — центр окружности (см. рисунок).


    \medskip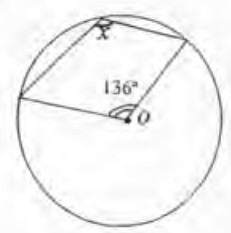

  4. Решите систему неравенств \[ \begin{cases} 2 - x > 0,\\ x + 3 > 0. \end{cases} \]

  5. В равнобедренную трапецию с боковой стороной \(8\) см и площадью \(48\) см\(^2\) вписана окружность. Найдите радиус этой окружности.

  6. Постройте график функции \[ y = x^2 - 6x + 5. \] По графику определите:
    1. при каких значениях \(x\) \(y > 0\);
    2. на каком промежутке функция убывает;
    3. уравнение оси симметрии параболы.


  7. Некоторое двузначное число на 18 больше суммы его цифр, а квадрат этого числа на 680 больше квадрата цифры единиц. Найдите это число.

  8. В треугольнике \(ABC\) площадь равна \(30\) см\(^2\). На стороне \(BC\) взята точка \(E\) так, что \(BE:EC = 2:3\), на стороне \(AC\) взята точка \(P\) так, что \(AP:PC = 1:2\). Найдите площадь четырёхугольника \(ABEP\).

  9. До просушки влажность зерна была 23%, а после просушки — 12%. На сколько процентов уменьшилась масса зерна после просушки?

  10. Упростите выражение \[ \sqrt{x + 2\sqrt{x - 1}} \;+\; \sqrt{x - 2\sqrt{x - 1}} \quad\text{при }1 \le x \le 2. \]
Материалы школы Юайти
youit.school ©

Решения задач



  1. Известно, что \[ a^3 > a^4. \] Тогда число \(a\) может быть равно \[ -3,\;-\tfrac{1}{3},\;3,\;\sqrt{3},\;\tfrac{1}{3}. \]
    Решение: Проверим каждое значение:
    \(a = \frac{1}{3}\): \(\left(\frac{1}{3}\right)^3 = \frac{1}{27}\), \(\left(\frac{1}{3}\right)^4 = \frac{1}{81}\).
    \(\frac{1}{27} > \frac{1}{81}\). Подходит.
    Остальные значения не удовлетворяют неравенству.
    Ответ: \(\frac{1}{3}\).
  2. На какой угол повернётся минутная стрелка за 5 минут?
    Решение: За 60 минут стрелка поворачивается на \(360^{\circ}\), значит за 1 минуту: \(360^{\circ} : 60 = 6^{\circ}\).
    За 5 минут: \(5 \cdot 6^{\circ} = 30^{\circ}\).
    Ответ: \(30^{\circ}\).
  3. Найдите величину угла \(x\), если \(O\) — центр окружности (см. рисунок).

    Решение: Угол, опирающийся на дугу \(120^{\circ}\), равен её половине:
    \(x = \frac{120^{\circ}}{2} = 60^{\circ}\).
    Ответ: \(60^{\circ}\).
  4. Решите систему неравенств \[ \begin{cases} 2 - x > 0,\\ x + 3 > 0. \end{cases} \] Решение:
    \( \begin{cases} x -3. \end{cases} \)
    Общее решение: \(-3 < x < 2\).
    Ответ: \(x \in (-3; 2)\).
  5. В равнобедренную трапецию с боковой стороной \(8\) см и площадью \(48\) см\(^2\) вписана окружность. Найдите радиус этой окружности.
    Решение: В трапецию можно вписать окружность, если суммы оснований равны сумме боковых сторон.
    Сумма оснований: \(8 + 8 = 16\) см. Площадь трапеции:
    \(\frac{16}{2} \cdot h = 48\) \(\Rightarrow\) \(h = 6\) см.
    Радиус окружности: \(\frac{h}{2} = 3\) см.
    Ответ: 3 см.
  6. Постройте график функции \[ y = x^2 - 6x + 5. \] По графику определите:
    1. При каких значениях \(x\) \(y > 0\):
      Решение: Корни уравнения \(x^2 -6x +5 =0\): \(x=1\) и \(x=5\). Парабола направлена вверх. \(y > 0\) при \(x 5\).
      Ответ: \(x \in (-\infty;1) \cup (5;+\infty)\).
    2. На каком промежутке функция убывает:
      Решение: Вершина параболы в точке \(x = \frac{6}{2} = 3\). Функция убывает при \(x \leq 3\).
      Ответ: \((-\infty;3]\).
    3. Уравнение оси симметрии параболы:
      Решение: Ось симметрии: \(x = 3\).
      Ответ: \(x = 3\).
  7. Некоторое двузначное число на 18 больше суммы его цифр, а квадрат этого числа на 680 больше квадрата цифры единиц. Найдите это число.
    Решение: Пусть число \(\overline{ab} = 10a + b\).
    Условия: \(10a + b = a + b + 18 \Rightarrow 9a = 18 \Rightarrow a = 2\).
    Второе условие: \((10a + b)^2 - b^2 = 680 \Rightarrow (20 + b)^2 - b^2 = 680\).
    Раскрываем: \(400 +40b = 680 \Rightarrow 40b = 280 \Rightarrow b =7\).
    Ответ: 27.
  8. В треугольнике \(ABC\) площадь равна \(30\) см\(^2\). На стороне \(BC\) взята точка \(E\) так, что \(BE:EC = 2:3\), на стороне \(AC\) взята точка \(P\) так, что \(AP:PC = 1:2\). Найдите площадь четырёхугольника \(ABEP\).
    Решение: Используем метод масс.
    Площадь треугольника \(ABE\): \(\frac{2}{5} \cdot 30 = 12\) см\(^2\).
    Площадь треугольника \(APB\): \(\frac{1}{3} \cdot 12 =4\) см\(^2\).
    Площадь \(ABEP = 12 - 4 =8\) см\(^2\).
    Ответ: 8 см\(^2\).
  9. До просушки влажность зерна была 23%, а после просушки — 12%. На сколько процентов уменьшилась масса зерна после просушки?
    Решение: Пусть исходная масса \(m\). Сухое вещество: \(0,77m\).
    После сушки масса стала \(M\): \(0,88M = 0,77m \Rightarrow M = \frac{77}{88}m = 0,875m\).
    Уменьшение массы: \(1 - 0,875 =0,125 =12,5\%\).
    Ответ: На 12,5%.
  10. Упростите выражение \[ \sqrt{x + 2\sqrt{x - 1}} \;+\; \sqrt{x - 2\sqrt{x - 1}} \quad\text{при }1 \le x \le 2. \] Решение: Заметим, что выражение можно записать как:
    \(\sqrt{(\sqrt{x-1} +1)^2} + \sqrt{(\sqrt{x-1} -1)^2}\).
    При \(1 \leq x \leq2\): \(\sqrt{x-1} -1 \leq0\), поэтому:
    \(\sqrt{x-1} +1 + (1 - \sqrt{x-1}) =2\).
    Ответ: 2.
Материалы школы Юайти