Могилёвский Лицей №1 из 9 в 10 класс 2014 год вариант 1
Печать
youit.school ©
МОГИЛЁВСКИЙ ЛИЦЕЙ №1
2014 год
Вариант 1
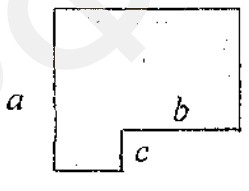
- От квадрата со стороной \(a\) отрезан прямоугольник со сторонами \(b\) и \(c\). Площадь полученной фигуры можно найти по формуле:
 \[
\text{1) }ab - bc;\quad
\text{2) }a^2 - bc;\quad
\text{3) }a^2 + bc;\quad
\text{4) }4a - 2(b + c).
\]
\[
\text{1) }ab - bc;\quad
\text{2) }a^2 - bc;\quad
\text{3) }a^2 + bc;\quad
\text{4) }4a - 2(b + c).
\]
- Из чисел \(3;\;2;\;\tfrac17;\;3{,}5;\;-6;\;5\) выберите числа, входящие в область определения выражения \[ \frac{1}{\sqrt{2x - 6}}. \]
- Переменные \(y\) и \(x\) обратно пропорциональны. Известно, что \(y = -6\) при \(x = 9\). Найдите значение \(y\) при \(x = -18\).
- Сумма гипотенузы и катета, лежащего в данном треугольнике против угла в \(30^\circ\), равна \(24\) см. Найдите гипотенузу.
- Решите уравнение \[ \frac{x - 4}{x} = \frac{2x + 10}{x + 4}. \]
- Окружность касается сторон \(AB\), \(BC\) и \(CD\) параллелограмма \(ABCD\). Касательная к окружности проходит через точку \(D\) и пересекает сторону \(AB\) в точке \(P\). Известно, что радиус окружности равен \(4\) см и площадь четырёхугольника \(DPBC\) равна \(40\) см\(^2\). Вычислите длину боковой стороны равнобедренной трапеции \(DPBC\).
- Решите систему неравенств: \[ \begin{cases} |2x + 3| \le 1,\\ x^2 + 4x + 3 \ge 0. \end{cases} \]
- Найдите биссектрису прямоугольного треугольника с катетами \(21\) см и \(28\) см, опущенную на гипотенузу.
- На сколько процентов изменится число, если его увеличили на \(20\%\), затем новое число уменьшили на \(25\%\) и полученное число увеличили на \(10\%\)?
- Найдите, при каких значениях переменной \(a\) уравнение \[ x^2 - 6\lvert x\rvert + 5 = a \] имеет ровно три различных корня.
Материалы школы Юайти
youit.school ©
Решения задач
- От квадрата со стороной \(a\) отрезан прямоугольник со сторонами \(b\) и \(c\). Площадь полученной фигуры равна разности площади квадрата и площади отрезанного прямоугольника: \[ a^2 - bc \] Ответ: $\boxed{2}.$
- Область определения выражения \(\frac{1}{\sqrt{2x - 6}}\) определяется неравенством \(2x - 6 > 0\) \(\Rightarrow x > 3\). Из предложенных чисел подходят \(3{,}5\) и \(5\).
Ответ: \(3{,}5;\ 5\). - Переменные \(y\) и \(x\) обратно пропорциональны: \(y = \frac{k}{x}\). Подставим \(x = 9\) и \(y = -6\): \[ -6 = \frac{k}{9} \Rightarrow k = -54 \] При \(x = -18\): \[ y = \frac{-54}{-18} = 3 \] Ответ: $\boxed{3}.$
- Гипотенуза \(c\) и катет \(c/2\) (лежащий напротив угла в \(30^\circ\)) дают сумму: \[ c + \frac{c}{2} = 24 \Rightarrow \frac{3c}{2} = 24 \Rightarrow c = 16\ \text{см} \] Ответ: $\boxed{16}.$
- Решаем уравнение:
\[
\frac{x - 4}{x} = \frac{2x + 10}{x + 4}
\]
После преобразований получим:
\[
x^2 + 10x + 16 = 0 \Rightarrow x_1 = -2,\ x_2 = -8
\]
Оба корня удовлетворяют ОДЗ.
Ответ: \(-2;\ -8\). - Трапеция \(DPBC\) имеет площадь \(40\ \text{см}^2\). Средняя линия трапеции равна \(5\ \text{см}\) (высота \(8\ \text{см}\), радиус окружности \(4\ \text{см}\)). Боковая сторона трапеции равна: \[ \sqrt{8^2 + \left(\frac{24 - 8}{2}\right)^2} = \sqrt{64 + 64} = \sqrt{128} = 8\sqrt{2}\ \text{см} \] Ответ: $\boxed{8\sqrt{2}}.$
- Решаем систему неравенств:
\[
\begin{cases}
|2x + 3| \le 1 \Rightarrow -2 \le x \le -1,\\
x^2 + 4x + 3 \ge 0 \Rightarrow x \le -3\ \text{или}\ x \ge -1.
\end{cases}
\]
Единственное решение: \(x = -1\).
Ответ: $\boxed{-1}.$ - Биссектриса прямоугольного треугольника с катетами \(21\) и \(28\ \text{см}\), опущенная на гипотенузу, находится по формуле: \[ l = \frac{2ab}{a + b} \cdot \cos\left(\frac{\pi}{4}\right) = \frac{2 \cdot 21 \cdot 28}{21 + 28} \cdot \frac{\sqrt{2}}{2} = 12\sqrt{2}\ \text{см} \] Ответ: $\boxed{12\sqrt{2}}.$
- Пусть исходное число \(N\). После изменений:
\[
N \rightarrow 1{,}2N \rightarrow 0{,}9N \rightarrow 0{,}99N
\]
Число уменьшилось на \(1\%\).
Ответ: $\boxed{1\%}.$ - Уравнение \(x^2 - 6|x| + 5 = a\) имеет три корня при значении параметра \(a = 5\). График функции пересекается прямой \(y = 5\) в трёх точках.
Ответ: $\boxed{5}.$
Материалы школы Юайти