Могилёвский Лицей №1 из 7 в 8 класс 2013 год вариант 1

МОГИЛЁВСКИЙ ЛИЦЕЙ №1

2013 год

Вариант 1

1. Выпишите натуральные числа: $7 ; 0 ; 1,7 ;-5 ; 3,5 ; 19 .$
2. Раскройте скобки и приведите подобные слагаемые: $a-(-(-5 a))$.
3. Какую цифру нужно поставить вместо * в числе $23 * 5$, чтобы полученное число делилось на 9? Ответ поясните.
4. Прямые $a$ и $b$ параллельны (см. рис.). Найдите углы 6 и 7, если $\angle 1=40^{\circ}$:
   
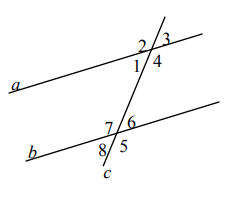
5. Решите уравнение: $\frac{x-1}{2}=\frac{4+2 x}{3}$.
6. Упростите: $\frac{\left(a^{3}\right)^{-2} \cdot\left(a^{-7}\right)^{-1}}{a^{-3}}$.
7. Периметр равнобедренного треугольника равен 32 см. Биссектриса, проведённая из его вершины, делит его на два треугольника, периметр каждого из которых равен 24 см. Найдите длину этой биссектрисы.
8. Упростите выражение: $\left(\frac{a}{a^{2}-25}-\frac{a-8}{a^{2}-10 a+25}\right): \frac{a-20}{(a-5)^{2}}$.
9. Ребята были в туристическом походе три дня. В первый день они прошли $40 \%$ всего маршрута, во второй день $-\frac{5}{8}$ оставшегося пути, a в третий день - последние 13,5 км. Найдите расстояние, пройденное ребятами за три дня.
10. Вычислите: $\frac{7}{1 \cdot 8}+\frac{7}{8 \cdot 15}+\frac{7}{15 \cdot 22}+\ldots+\frac{7}{57 \cdot 64}$.

Решения задач

1. Выпишите натуральные числа: $7 ; 0 ; 1,7 ;-5 ; 3,5 ; 19 .$
   Решение: Натуральные числа — целые положительные. Из предложенных подходят: 7; 19.
   Ответ: 7;19.
2. Раскройте скобки и приведите подобные слагаемые: $a-(-(-5 a))$.
   Решение: Последовательно раскрываем скобки:
   $a - (-(-5a)) = a - (5a) = a - 5a = -4a$.
   Ответ: $-4a$.
3. Какую цифру нужно поставить вместо * в числе $23 * 5$, чтобы полученное число делилось на 9? Ответ поясните.
   Решение: Для делимости на 9 сумма цифр должна делиться на 9. Сумма известных цифр: $2 + 3 + 5 = 10$. Тогда $10 + *$ должно делиться на 9. Ближайшее кратное 9 — 18. Значит, $* = 8$.
   Ответ: 8.
4. Прямые $a$ и $b$ параллельны (см. рис.). Найдите углы 6 и 7, если $\angle 1=40^{\circ}$:
   
   Решение: $\angle 6$ соответствует $\angle 1$ как накрест лежащий при параллельных прямых, поэтому $\angle 6 = 40^{\circ}$. $\angle 7$ смежен с $\angle 6$, значит $\angle 7 = 180^{\circ} - 40^{\circ} = 140^{\circ}$.
   Ответ: $40^{\circ}$; $140^{\circ}$.
5. Решите уравнение: $\frac{x-1}{2}=\frac{4+2 x}{3}$.
   Решение: Умножим обе части на 6:
   $3(x - 1) = 2(4 + 2x)$
   $3x - 3 = 8 + 4x$
   $-x = 11$
   $x = -11$.
   Ответ: $-11$.
6. Упростите: $\frac{\left(a^{3}\right)^{-2} \cdot\left(a^{-7}\right)^{-1}}{a^{-3}}$.
   Решение: Упростим степени:
   $\frac{a^{-6} \cdot a^{7}}{a^{-3}} = \frac{a^{1}}{a^{-3}} = a^{1 + 3} = a^{4}$.
   Ответ: $a^{4}$.
7. Периметр равнобедренного треугольника равен 32 см. Биссектриса, проведённая из его вершины, делит его на два треугольника, периметр каждого из которых равен 24 см. Найдите длину этой биссектрисы.
   Решение: Пусть треугольник $ABC$ с основанием $AC$, $AB = BC = x$, $AC = y$. Тогда:
   $2x + y = 32$ (1)
   Периметры треугольников $ABD$ и $CBD$ (где $BD$ — биссектриса):
   $x + BD + \frac{y}{2} = 24$ (2)
   Сложим уравнения для обоих треугольников:
   $2x + 2BD + y = 48$
   Из (1) подставим $2x + y = 32$:
   $32 + 2BD = 48 \Rightarrow BD = 8$ см.
   Ответ: 8 см.
8. Упростите выражение: $\left(\frac{a}{a^{2}-25}-\frac{a-8}{a^{2}-10 a+25}\right): \frac{a-20}{(a-5)^{2}}$.
   Решение: Разложим знаменатели:
   $\left(\frac{a}{(a-5)(a+5)} - \frac{a-8}{(a-5)^2}\right) \cdot \frac{(a-5)^2}{a-20}$
   Приведем к общему знаменателю:
   $\frac{a(a-5) - (a-8)(a+5)}{(a-5)^2(a+5)} \cdot \frac{(a-5)^2}{a-20} = \frac{-2a + 40}{(a+5)(a-20)} = -\frac{2}{a+5}$.
   Ответ: $-\frac{2}{a+5}$.
9. Ребята были в туристическом походе три дня. В первый день они прошли $40 \%$ всего маршрута, во второй день $-\frac{5}{8}$ оставшегося пути, a в третий день - последние 13,5 км. Найдите расстояние, пройденное ребятами за три дня.
   Решение: Пусть весь путь $x$ км. После первого дня осталось $0,6x$ км. Во второй день прошли $\frac{5}{8} \cdot 0,6x = 0,375x$ км. Остаток:
   $0,6x - 0,375x = 0,225x = 13,5$ км
   $x = \frac{13,5}{0,225} = 60$ км.
   Ответ: 60 км.
10. Вычислите: $\frac{7}{1 \cdot 8}+\frac{7}{8 \cdot 15}+\frac{7}{15 \cdot 22}+\ldots+\frac{7}{57 \cdot 64}$.
    Решение: Представим каждое слагаемое как разность:
    $\frac{7}{n(n+7)} = \frac{1}{n} - \frac{1}{n+7}$
    Сумма примет вид:
    $\left(1 - \frac{1}{8}\right) + \left(\frac{1}{8} - \frac{1}{15}\right) + \ldots + \left(\frac{1}{57} - \frac{1}{64}\right) = 1 - \frac{1}{64} = \frac{63}{64}$.
    Ответ: $\frac{63}{64}$.