Могилёвский Лицей №1 из 6 в 7 класс 2014 год вариант 1

МОГИЛЁВСКИЙ ЛИЦЕЙ №1

2014 год

Вариант 1

1. Вычислите значение выражения $\frac{2014 \cdot 2,014}{201,4 \cdot 20,14}$ :
   1) 0,01 ; 2) 0,1 ; 3) 1 ; 4) 10 ; 5) 100 .
2. Шесть одинаковых кругов вписаны в прямоугольник так, как показано на рисунке. Вершины меньшего прямоугольника находятся в центрах двух левых и двух правых кругов (см. рис.). Периметр меньшего прямоугольника равен 60 см. Найдите периметр прямоугольника.
   
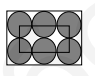
   1) $160 \mathrm{~cm}$; 2) $140 \mathrm{~cm}$; 3) $120 \mathrm{~cm}$; 4) $100 \mathrm{~cm}$; 5) $80 \mathrm{~cm}$
3. Пусть на координатной плоскости отмечены точки $A(2014,2015)$, $B(2015,2014)$, $C(-2014,-2015)$, $D(2014,-2015)$ и $E(2015,-2014) .$ Тогда горизонтальным (параллельным оси $O x$ ) является отрезок:
   1) $A D$; 2) $B E$; 3) $B C$; 4) $C D$; 5) $A B$.
4. Пятизначное число 24X8Y делится на 4, 5 и 9. Чему равна сумма цифр X и Y?
   1) 13 ; 2) 10 ; 3) 9; 4) 5 ; 5) $4 .$
5. Чтобы получить $8^{8}$ нужно $4^{4}$ возвести в степень:
   1) 2 ; 2) 3; 3) 4 ; 4) 6 ; 5) 8 .
6. При каком значении $c$ уравнение $\left(c^{2}-1\right) x=c-1$:
   1) имеет единственное решение; 2) имеет бесконечное множество решений; 3) не имеет решений.
   Ответ поясните.
7. Три прямые пересекаются в одной точке (см. рис.). Найдите $\angle A O B$, если $\angle A O C=108^{\circ}$, $\angle C O E=124^{\circ}$.
   
   
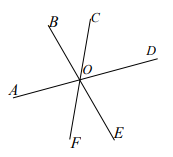
8. Докажите, что при всех действительных значениях $x$ и $y$ выражение $x^{2}+y^{2}-16 x+14 y+137$ принимает положительное значение.
9. Докажите тождество $\frac{a^{2}-a c^{2}+2 c^{2}-4}{a^{2}+2 a+2 c^{2}-c^{4}}-\frac{a^{2}-4 a+4}{a^{2}+a c^{2}-2 a-2 c^{2}}=0$.
10. Найдите все целые значения $n$, при которых дробь $\frac{7 n^{2}+3 n-10}{n}$ принимает натуральные значения.

Решения задач

1. Вычислите значение выражения $\frac{2014 \cdot 2,014}{201,4 \cdot 20,14}$.
   Решение: Упростим выражение:
   $\frac{2014 \cdot 2,014}{201,4 \cdot 20,14} = \frac{2014}{201,4} \cdot \frac{2,014}{20,14} = 10 \cdot 0,1 = 1$.
   Ответ: 3) 1.
   
   
2. Найдите периметр прямоугольника, если периметр меньшего прямоугольника равен 60 см.
   Решение: Пусть радиус круга $r$. Меньший прямоугольник имеет стороны $4r$ и $2r$, его периметр:
   $2(4r + 2r) = 12r = 60 \Rightarrow r = 5$ см.
   Больший прямоугольник имеет стороны $6r$ и $4r$, его периметр:
   $2(6r + 4r) = 20r = 20 \cdot 5 = 100$ см.
   Ответ: 4) $100 \mathrm{~cm}$.
   
   
3. Определите горизонтальный отрезок.
   Решение: Горизонтальный отрезок имеет одинаковые $y$-координаты. Для точек $C(-2014,-2015)$ и $D(2014,-2015)$ $y = -2015$.
   Ответ: 4) $C D$.
   
   
4. Найдите сумму цифр $X$ и $Y$ для числа $24X8Y$, делящегося на 4, 5 и 9.
   Решение:
   • Делимость на 5: $Y = 0$ или $5$.
   • Делимость на 4: $80$ делится на 4 $\Rightarrow Y = 0$.
   • Делимость на 9: $2 + 4 + X + 8 + 0 = 14 + X \equiv 0 \pmod{9} \Rightarrow X = 4$.
   Сумма: $X + Y = 4 + 0 = 4$.
   Ответ: 5) 4.
   
   
5. Определите степень для выражения $4^{4}$.
   Решение: $8^{8} = (2^{3})^{8} = 2^{24}$; $4^{4} = (2^{2})^{4} = 2^{8}$.
   $(2^{8})^{3} = 2^{24} \Rightarrow$ степень: 3.
   Ответ: 2) 3.
   
   
6. Исследуйте уравнение $\left(c^{2}-1\right) x=c-1$.
   Решение:
   • При $c \neq \pm1$: единственное решение $x = \frac{1}{c+1}$.
   • При $c = 1$: бесконечно много решений.
   • При $c = -1$: нет решений.
   Ответ: 1) $c \neq \pm1$; 2) $c = 1$; 3) $c = -1$.
   
   
7. Найдите $\angle A O B$.
   Решение: Сумма углов вокруг точки $O$ равна $360^{\circ}$. Учитывая $\angle A O C = 108^{\circ}$ и $\angle C O E = 124^{\circ}$, угол $\angle A O B$ равен:
   $360^{\circ} - 108^{\circ} - 124^{\circ} - 124^{\circ} = 52^{\circ}$ (вертикальные углы).
   Ответ: $52^{\circ}$.
   
   
8. Докажите положительность выражения $x^{2}+y^{2}-16x+14y+137$.
   Решение: Выделим полные квадраты:
   $(x-8)^{2} + (y+7)^{2} + 24 \geq 24 > 0$.
   Ответ: Выражение всегда положительно.
   
   
9. Докажите тождество.
   Решение: Упростим дроби:
   $\frac{(a-2)(a+2 -c^{2})}{(a +c^{2})(a +2 -c^{2})} - \frac{(a-2)^{2}}{(a-2)(a +c^{2})} = \frac{a-2}{a +c^{2}} - \frac{a-2}{a +c^{2}} = 0$.
   Тождество доказано.
   
   
10. Найдите целые $n$ для дроби $\frac{7n^{2}+3n-10}{n}$.
    Решение: Условие делимости $10$ на $n$ дает $n = \pm1, \pm2, \pm5, \pm10$. Проверка натуральности:
    $n = -1, 2, 5, 10$ (значения $6, 6, 36, 72$ соответственно).
    Ответ: $-1; 2; 5; 10$.