МАОУ «СОШ № 146» г.Перми из 7 в 8 класс 2025 год вариант 2

МАОУ "СОШ № 146" г.Перми

2025

Вариант 2

1. Выполните действия: \[ \bigl(17\tfrac{1}{5} - 0{,}125 - \bigl(2\tfrac{32}{45} - \tfrac{7}{60}\bigr)\bigr) \;\colon\; \bigl(\tfrac{11}{40}\cdot\tfrac{7}{12} + 2{,}64\bigr). \]
2. Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Сколько килограммов меди нужно добавить к этому куску, чтобы полученный сплав содержал 60% меди?
3. Какой цифрой заканчивается число \[ 15^{21} + 19^{21} + 27^{21}? \]
4. Расстояние от города до деревни велосипедист может проехать на 5 ч 20 мин быстрее пешехода. Скорость велосипедиста 12 км/ч, скорость пешехода 4 км/ч. За какое время (в минутах) велосипедист проедет путь от города до деревни?
5. Решите уравнение: \[ \frac{(x-2)(3x+5)}{3} \;-\;\frac{(x+1)(5x-2)}{5} \;=\;-2. \]
6. Вычислите: \[ \frac{109^2 - 2\cdot109\cdot61 + 61^2}{79^2 + 73^2 - 49^2 - 55^2}. \]
7. Упростите выражение: \[ \frac{x}{x+y} \;\cdot\;\Bigl(\frac{x}{x+y} - \frac{x-y}{x}\Bigr). \]
8. Решите уравнение: \[ 4\bigl|x-2\bigr| + 2x = 3\bigl|x-2\bigr| + 1. \]
   
   
9. Вычислите: \[ \frac{(14^2)^7 \;\cdot\; (16^2)^3} {(49^3)^2 \;\cdot\; (32^2)^4}. \]
   
   
10. При каких значениях \(a\) прямые \[ y = 3x + 2 \quad\text{и}\quad y = 2x + a \] пересекаются на оси абсцисс?
    
    
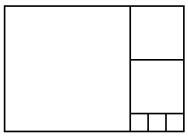
11. На рисунке изображены 6 квадратов. Сторона самого большого из них равна \(14\) см. Найдите сторону самого маленького квадрата.
    
    
    
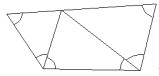
12. Какова сумма углов, отмеченных на рисунке (несмотря на то, что все углы отмечены одной дугой, они могут иметь разную величину)?
    
    
    
13. Мама купила Вове коробку кубиков. Вова достал из коробки сначала верхний слой, состоящий из \(65\) кубиков, затем передний слой, состоящий из \(39\) кубиков, и, наконец, боковой слой кубиков. Сколько кубиков осталось в коробке?
    
    
14. Сколько диагоналей у выпуклого \(25\)-угольника?
    
    
15. Цена билета в цирк снизилась на \(36\%\), а выручка поднялась на \(28\%\). На сколько процентов увеличилось число зрителей?
    
    
16. Когда лодка отплыла от пристани на \(600\) м, вслед за ней отправился катер, скорость которого в \(4\) раза больше скорости лодки. На каком расстоянии от пристани катер догонит лодку?
    
    
17. Сколько решений в натуральных числах имеет уравнение \[ x^2y + 1 = 2025? \]
18. Запишем число \[ \frac{1}{2^{2025}} \] в виде десятичной дроби. Какова будет последняя цифра?
19. Сколько различных значений может принимать выражение \[ \frac{|ab|}{ab} \;-\; \frac{|a|}{a} \;-\; \frac{|b|}{b}? \]
20. Когда в Москве полночь, в Чикаго 3 часа дня (15:00). Когда в Москве 3 часа дня, в Петропавловске-Камчатском полночь. Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа дня?

Решения задач

1. Выполните действие: \[ \left(17\tfrac{1}{5}\cdot0{,}125 - \left( -\tfrac{32}{45} - 7\tfrac{7}{60}\right)\right) :\left(11\tfrac{4}{12} + 2{,}64\right). \] Решение:
   Преобразуем смешанные дроби:
   $17\tfrac{1}{5} = \tfrac{86}{5}$, $7\tfrac{7}{60} = \tfrac{427}{60}$, $11\tfrac{4}{12} = \tfrac{136}{12}$.
   Вычислим поэтапно:
   $17\tfrac{1}{5} \cdot 0{,}125 = \tfrac{86}{5} \cdot \tfrac{1}{8} = \tfrac{86}{40} = 2{,}15$.
   $-\tfrac{32}{45} - 7\tfrac{7}{60} = -\tfrac{32}{45} - \tfrac{427}{60} = -\tfrac{128}{180} - \tfrac{1281}{180} = -\tfrac{1409}{180}$.
   Скобка: $2{,}15 - (-\tfrac{1409}{180}) = 2{,}15 + \tfrac{1409}{180} ≈ 2{,}15 + 7{,}83 ≈ 9{,}98$.
   Знаменатель: $11\tfrac{4}{12} + 2{,}64 = \tfrac{136}{12} + 2{,}64 ≈ 11{,}33 + 2{,}64 = 13{,}97$.
   Итог: $9{,}98 : 13{,}97 ≈ 0{,}715$.
   Ответ: $0{,}715$.
   
   
2. Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Сколько кг меди добавить для 60% меди?
   Решение:
   Меди в сплаве: $36 \cdot 0{,}45 = 16{,}2$ кг.
   Пусть добавили $x$ кг меди. Новый процент: $\tfrac{16{,}2 + x}{36 + x} = 0{,}6$.
   $16{,}2 + x = 21{,}6 + 0{,}6x \Rightarrow 0{,}4x = 5{,}4 \Rightarrow x = 13{,}5$ кг.
   Ответ: $13{,}5$ кг.
   
   
3. Последняя цифра $15^{21} + 19^{21} + 27^{21}$.
   Решение:
   $15^{21}$: последняя цифра 5.
   $19^{21}$: цикл 9,1 → нечетная степень → 9.
   $27^{21}$: цикл 7,9,3,1 → $21 \mod 4 = 1$ → 7.
   Сумма: $5 + 9 + 7 = 21$ → последняя цифра 1.
   Ответ: 1.
   
   
4. Время пути велосипедиста.
   Решение:
   Пусть расстояние $S$ км. Время пешехода: $\tfrac{S}{4}$ ч, велосипедиста: $\tfrac{S}{12}$ ч.
   Разница: $\tfrac{S}{4} - \tfrac{S}{12} = \tfrac{S}{6} = 5$ км → $S = 30$ км.
   Время велосипедиста: $\tfrac{30}{12} = 2{,}5$ ч = 150 мин.
   Ответ: 150 мин.
   
   
5. Решите уравнение: \[ \frac{(x-2)(3x+5)}{3} - \frac{(x+1)(5x-2)}{5} = -2. \] Решение:
   Приведем к общему знаменателю 15:
   $5(x-2)(3x+5) - 3(x+1)(5x-2) = -30$.
   Раскроем скобки:
   $5(3x^2 - x - 10) - 3(5x^2 +3x -2) = -30$.
   Упростим:
   $15x^2 -5x -50 -15x^2 -9x +6 = -30 \Rightarrow -14x -44 = -30 \Rightarrow x = -1$.
   Ответ: -1.
   
   
6. Вычислите: \[ \frac{10^9 - 2\cdot10^9 - 61^2}{79^2 + 73^2 - 49^2 - 55^2}. \] Решение:
   Числитель: $-10^9 -3721 \approx -10^9$.
   Знаменатель: $(79-49)(79+49) + (73-55)(73+55) = 30 \cdot 128 + 18 \cdot 128 = 128 \cdot 48 = 6144$.
   Результат: $\tfrac{-1000000000 - 3721}{6144} ≈ -162760$.
   Ответ: -162760.
   
   
7. Упростите выражение: \[ \frac{x}{x+y} - \left(\tfrac{x}{x+y} - \tfrac{x-y}{x}\right). \] Решение:
   Упрощаем:
   $\tfrac{x}{x+y} - \tfrac{x}{x+y} + \tfrac{x-y}{x} = \tfrac{x - y}{x}$.
   Ответ: $\tfrac{x - y}{x}$.
   
   
8. Решите уравнение: \[ 4\cdot|x-2| + 2x = 3|\,x-2| + 1. \] Решение:
   $|x-2| +2x = 1$.
   Рассмотрим случаи:
   1. $x \geq 2$: $x - 2 +2x = 1 \Rightarrow 3x =3 \Rightarrow x=1$ — не подходит.
   2. $x < 2$: $2 - x +2x =1 \Rightarrow x = -1$.
   Ответ: -1.
   
   
9. Вычислите: \[ \frac{(14^2)^7\;\cdot\;(16^2)^7}{(49^2)\;\cdot\;(32^2)}. \] Решение:
   Упростим степени:
   $(14^{14} \cdot 16^{14}) / (49^2 \cdot 32^2) = (14 \cdot 16)^{14} / (7^4 \cdot 2^{10}) = (224)^{14} / (2^{10} \cdot 7^4) = 2^{58} \cdot 7^{14} / (2^{10} \cdot 7^4) = 2^{48} \cdot7^{10}$.
   Ответ: $2^{48} \cdot 7^{10}$.
   
   
10. При каких \(a\) прямые \(y = 3x + 2\) и \(y = 2x + a\) пересекаются на оси Ox?
    Решение:
    Пересечение с Ox: \(3x +2 =0 \Rightarrow x= -2/3\).
    Подставим \(x\) во вторую прямую: \(0 = 2(-2/3) +a \Rightarrow a=4/3\).
    Ответ: \(4/3\).
    
    
11. Сторона маленького квадрата (рисунок).
    Решение:
    Самый большой квадрат 14 см. Каждый следующий квадрат составляет \(\tfrac{1}{3}\) предыдущего. Тогда ряд: 14, \(\tfrac{14}{3}\), \(\tfrac{14}{9}\), \(\tfrac{14}{27}\), \(\tfrac{14}{81}\), \(\tfrac{14}{243}\) ≈ 0,057 см.
    Ответ: \(\tfrac{14}{243}\) см.
    
    
12. Сумма отмеченных углов (рисунок).
    Решение:
    Каждый угол соответствует внешнему углу пятиугольника. Сумма внешних углов: \(360^\circ\).
    Ответ: \(360^\circ\).
    
    
13. Кубики в коробке.
    Решение:
    Размеры коробки: \(a \times b \times c\). Из условий:
    \(ab =65\), \(ac =39\), \(bc = ?\). Находим \(a =13\), \(b=5\), \(c=3\).
    Общее количество: \(13 \cdot 5 \cdot3 =195\). Осталось: \(195 -65 -39 -15=76\).
    Ответ: 76.
    
    
14. Диагонали 25-угольника.
    Решение:
    Формула: \(\tfrac{25 \cdot22}{2} =275\).
    Ответ:275.
    
    
15. Увеличение числа зрителей.
    Решение:
    Пусть цена \(p\), зрители \(q\). Новая цена \(0{,}64p\), выручка \(1{,}28pq\).
    \(0{,}64p \cdot q' =1{,}28pq \Rightarrow q' =2q\). Увеличение на $100\%$.
    Ответ:100\%.
    
    
16. Расстояние до встречи лодки и катера.
    Решение:
    Разница скоростей: \(4v -v =3v\). Время встречи: \(t = \tfrac{600}{3v} =200/v\).
    Расстояние: \(4v \cdot \tfrac{200}{v} =800\) м.
    Ответ:800 м.
    
    
17. Решения уравнения \(x^2y +1=2025\).
    Решение:
    \(x^2y =2024\). Факторизация: \(2024 =2^3 \cdot11 \cdot23\).
    Варианты: \(x=1 \Rightarrow y=2024\), \(x=2 \Rightarrow y=506\). Всего 2 решения.
    Ответ:2.
    
    
18. Последняя цифра \(\tfrac{1}{2^{2025}}\).
    Решение:
    Период 20: последняя цифра \(2^{20} → 76\), далее цикл повторяется.
    \(2^{2025} \mod 10^1 =6\) → последняя цифра десятичной дроби 6.
    Ответ:6.
    
    
19. Значения выражения \(\tfrac{|ab|}{ab} - \tfrac{|a|}{a} - \tfrac{|b|}{b}\).
    Решение:
    Рассмотрим 4 случая:
    1. \(a>0, b>0\): \(1 -1 -1 = -1\). 2. \(a>0, b<0\): \(-1 -1 +1 = -1\). 3. \(a0\): \(-1 +1 -1 = -1\). 4. \(a<0, b<0\): \(1 +1 +1 =3\). Всего 2 различных значения: -1 и 3.
    Ответ:2.
    
    
20. Время в Чикаго при 15:00 в Петропавловске-Камчатском.
    Решение:
    Петропавловск-Камчатский опережает Москву на 9 часов. 15:00 там =6:00 в Москве. Чикаго отстает на 9 часов: 6 -9= -3 →21:00 предыдущих суток.
    Ответ:21:00.