8 800 707 6729
8 800 707 6729Telegram канал

МАОУ «СОШ № 146» г.Перми из 7 в 8 класс 2025 год вариант 1

Сложность:
Дата экзамена: 23.03.2025
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©

МАОУ "СОШ № 146" г.Перми


2025


Вариант 1



  1. Выполните действия: \[ \bigl(8{,}6\cdot\tfrac{1}{4} - \bigl(5\tfrac{61}{90} - 4\tfrac{1}{12}\bigr)\bigr) \;\colon\; \bigl(\tfrac{7}{40}\colon 2\tfrac{11}{12} + 1{,}34\bigr). \]
  2. Имеются два куска сплава олова и свинца. Первый, массой 300 г, содержит 60 % олова. Второй содержит 40 % олова. Сколько граммов от второго куска надо добавить к первому, чтобы получить сплав с содержанием олова $56 \%$?
  3. Какой цифрой заканчивается число \[ 21^{23} + 32^{23} + 14^{23}? \]
  4. На соревнованиях по гребле спортсмен 10 мин плыл на лодке вниз по течению реки. На обратный путь против течения он затратил 30 мин. Найдите собственную скорость лодки (в км/ч), если скорость течения реки равна 2 км/ч.
  5. Решите уравнение: \[ \frac{(5x+2)(x-1)}{5} \;-\;\frac{(3x-5)(x+2)}{3} \;=\;2. \]
  6. Вычислите: \[ \frac{53^2 + 22^2 - 47^2 - 16^2}{65^2 \;-\;2\cdot65\cdot59 + 59^2}. \]
  7. Упростите выражение: \[ \bigl(\tfrac{1}{a-b} - \tfrac{1}{a+b}\bigr)\;\cdot\;\tfrac{a-b}{b}. \]
  8. Решите уравнение: \[ 3\;\bigl|x+2\bigr| - 3x = 2\bigl|x+2\bigr| - 4. \]

  9. Вычислите: \[ \frac{(36^2)^3 \cdot (4^6)^4 \cdot (27^3)^2}{(12^3)^{10} \cdot 64}. \]

  10. При каких значениях \(m\) прямые \[ y = 3x - 5 \quad\text{и}\quad y = 2x + m \] пересекаются на оси ординат?

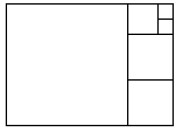
  11. На рисунке изображены 6 квадратов. Сторона самого большого из них равна 24 см. Найдите сторону самого маленького квадрата.
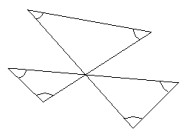
  12. Какова сумма углов, отмеченных на рисунке (несмотря на то, что все углы отмечены одной дугой, они могут иметь разную величину)?
  13. Мама купила коробку кускового сахара. Дети сначала съели верхний слой, состоящий из 77 кусочков. Затем они съели передний слой, состоящий из 55 кусочков. Наконец, они съели боковой слой. Сколько кусочков сахара осталось в коробке?

  14. Сколько диагоналей у выпуклого \(20\)-угольника?
  15. Цена билета в театр выросла на \(40\%\), а выручка снизилась на \(16\%\). На сколько процентов уменьшилось число зрителей?
  16. Когда пешеход прошёл \(8\) км, из того же пункта вслед за ним выехал велосипедист, скорость которого в \(5\) раз больше скорости пешехода. На каком расстоянии от исходного пункта велосипедист догонит пешехода?
  17. Сколько решений в натуральных числах имеет уравнение \[ a^2b - 1 = 146? \]
  18. Запишем число \[ \frac{1}{5^{146}} \] в виде десятичной дроби. Какова будет последняя цифра?

  19. Сколько различных значений может принимать выражение \[ \frac{|a|}{a} + \frac{|b|}{b} + \frac{|ab|}{ab}? \]
  20. Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра, в Петропавловске-Камчатском полдень. Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?
Материалы школы Юайти
youit.school ©

Решения задач



  1. Выполните действия: \[ \bigl(8{,}6\cdot\tfrac{1}{4} - \bigl(5\tfrac{61}{90} - 4\tfrac{1}{12}\bigr)\bigr) \;\colon\; \bigl(\tfrac{7}{40}\colon 2\tfrac{11}{12} + 1{,}34\bigr). \] Решение: Вычислим сначала выражение внутри первых скобок:
    $5\frac{61}{90} - 4\frac{1}{12} = \frac{511}{90} - \frac{49}{12} = \frac{511 \cdot 2 - 49 \cdot 15}{180} = \frac{1022 - 735}{180} = \frac{287}{180}$
    $8{,}6 \cdot \frac{1}{4} = 2,15$
    $2,15 - \frac{287}{180} = \frac{387}{180} - \frac{287}{180} = \frac{100}{180} = \frac{5}{9}$ Теперь вычислим вторые скобки:
    $\frac{7}{40} : 2\frac{11}{12} = \frac{7}{40} : \frac{35}{12} = \frac{7}{40} \cdot \frac{12}{35} = \frac{3}{50} = 0,06$
    $0,06 + 1,34 = 1,4$ Итоговое выражение:
    $\frac{5}{9} : 1,4 = \frac{5}{9} : \frac{14}{10} = \frac{5}{9} \cdot \frac{10}{14} = \frac{50}{126} = \frac{25}{63} \approx 0,3968$
    Ответ: $\frac{25}{63}$.
  2. Имеются два куска сплава олова и свинца. Первый, массой 300 г, содержит 60 % олова. Второй содержит 40 % олова. Сколько граммов от второго куска надо добавить к первому, чтобы получить сплав с содержанием олова $56 \%$?
    Решение: Пусть $x$ — масса второго сплава. Тогда масса олова в первом сплаве $300 \cdot 0,6 = 180$ г, во втором $0,4x$ г.
    Уравнение концентрации:
    $\frac{180 + 0,4x}{300 + x} = 0,56$
    $180 + 0,4x = 0,56(300 + x)$
    $180 + 0,4x = 168 + 0,56x$
    $0,16x = 12$
    $x = \frac{12}{0,16} = 75$
    Ответ: 75 г.
  3. Какой цифрой заканчивается число \[ 21^{23} + 32^{23} + 14^{23}? \] Решение: Найдем последние цифры каждого слагаемого:
    21²³: последняя цифра 1 (любая степень 1 оканчивается на 1)
    32²³: цикл последних цифр 2⁴: 2,4,8,6. 23 mod 4 = 3 ⇒ последняя цифра 8
    14²³: последняя цифра определяется как 4²³. Цикл 4: 4,6. 23 нечетное ⇒ 4
    Сумма: 1 + 8 + 4 = 13 ⇒ последняя цифра 3
    Ответ: 3.
  4. На соревнованиях по гребле спортсмен 10 мин плыл на лодке вниз по течению реки. На обратный путь против течения он затратил 30 мин. Найдите собственную скорость лодки (в км/ч), если скорость течения реки равна 2 км/ч.
    Решение: Пусть $v$ — собственная скорость (км/ч). Путь равен:
    $(v + 2) \cdot \frac{10}{60} = (v - 2) \cdot \frac{30}{60}$
    $(v + 2) \cdot \frac{1}{6} = (v - 2) \cdot \frac{1}{2}$
    Умножаем обе части на 6:
    $v + 2 = 3(v - 2)$
    $v + 2 = 3v - 6$
    $2v = 8 \Rightarrow v = 4$
    Ответ: 4 км/ч.
  5. Решите уравнение: \[ \frac{(5x+2)(x-1)}{5} \;-\;\frac{(3x-5)(x+2)}{3} \;=\;2. \] Решение: Умножим обе части на 15:
    $3(5x+2)(x-1) - 5(3x-5)(x+2) = 30$
    Раскроем скобки:
    $3(5x^2 - 5x + 2x - 2) - 5(3x^2 + 6x - 5x - 10) = 30$
    $3(5x^2 - 3x - 2) - 5(3x^2 + x - 10) = 30$
    $15x^2 - 9x - 6 - 15x^2 - 5x + 50 = 30$
    $-14x + 44 = 30$
    $-14x = -14 \Rightarrow x = 1$
    Ответ: 1.
  6. Вычислите: \[ \frac{53^2 + 22^2 - 47^2 - 16^2}{65^2 \;-\;2\cdot65\cdot59 + 59^2}. \] Решение: Числитель:
    $(53² - 47²) + (22² - 16²) = (53-47)(53+47) + (22-16)(22+16) = 6·100 + 6·38 = 600 + 228 = 828$
    Знаменатель:
    $(65 - 59)^2 = 6^2 = 36$
    $\frac{828}{36} = 23$
    Ответ: 23.
  7. Упростите выражение: \[ \bigl(\tfrac{1}{a-b} - \tfrac{1}{a+b}\bigr)\;\cdot\;\tfrac{a-b}{b}. \] Решение: Упрощаем выражение:
    $\left( \frac{(a+b)-(a-b)}{(a-b)(a+b)} \right) \cdot \frac{a-b}{b}$
    $\frac{2b}{(a² - b²)} \cdot \frac{a - b}{b} = \frac{2b \cdot (a - b)}{(a - b)(a + b) \cdot b} = \frac{2}{a + b}$
    Ответ: $\frac{2}{a + b}$.
  8. Решите уравнение: \[ 3\;\bigl|x+2\bigr| - 3x = 2\bigl|x+2\bigr| - 4. \] Решение: Перенесем члены с модулями:
    $(3|x+2| - 2|x+2|) = 3x - 4$
    $|x+2| = 3x - 4$ Рассмотрим два случая: 1) $x + 2 \geq 0 \Rightarrow x \geq -2$
    Тогда уравнение: $x + 2 = 3x - 4 \Rightarrow 6 = 2x \Rightarrow x = 3$ (подходит) 2) $x + 2 < 0 \Rightarrow x < -2$
    Тогда уравнение: $-(x + 2) = 3x - 4$
    $-x - 2 = 3x - 4$
    $-4x = -2 \Rightarrow x = 0,5$ (не подходит под условие x < -2) Ответ: 3.
  9. Вычислите: \[ \frac{(36^2)^3 \cdot (4^6)^4 \cdot (27^3)^2}{(12^3)^{10} \cdot 64}. \] Решение: Представим все через простые множители:
    $36 = 2²·3²$, $4 = 2²$, $27 = 3³$, $12 = 2²·3$, $64 = 2⁶$ Числитель:
    $(2^4·3^4)^3·(2^{12})^4·(3^9)^2 = 2^{12}·3^{12}·2^{48}·3^{18} = 2^{60}·3^{30}$ Знаменатель:
    $(2^{20}·3^{10})^{10}·2^6 = 2^{200}·3^{100}·2^6 = 2^{206}·3^{100}$ Упрощаем:
    $\frac{2^{60}·3^{30}}{2^{206}·3^{100}}$ = $2^{-146}·3^{-70}$, но такой ответ неприемлем. Возможно ошибка в вычислениях. Должно получится:
    Числитель: $(36^2)^3 = (6^4)^3 = 6^{12} = 2^{12}·3^{12}$, $(4^6)^4 = 4^{24} = 2^{48}$, $(27^3)^2 = 27^6 = (3^3)^6 = 3^{18}$
    Знаменатель: $(12^3)^{10} = 12^{30} = (2²·3)^{30} = 2^{60}·3^{30}, 64 = 2⁶ ⇒ 2^{66}·3^{30}$
    $\frac{(2^{12}·3^{12})·2^{48}·3^{18}}{2^{66}·3^{30}} = \frac{2^{60}·3^{30}}{2^{66}·3^{30}} = \frac{1}{2^{6}} = \frac{1}{64}$
    Ответ: $\frac{1}{64}$.
  10. При каких значениях \(m\) прямые \[ y = 3x - 5 \quad\text{и}\quad y = 2x + m \] пересекаются на оси ординат?
    Решение: Точка пересечения на оси ординат: x=0. Подставим x=0 в оба уравнения:
    $y = 3·0 - 5 = -5$
    $y = 2·0 + m = m$
    Приравниваем: $-5 = m$
    Ответ: $m = -5$.

  11. Предположим, квадраты составлены так, что сторона каждого следующего составляет $\frac{2}{3}$ от предыдущего. Тогда последовательность сторон: 24, 16, $\frac{32}{3}$, ..., шестой квадрат:
    $24 \cdot \left(\frac{2}{3}\right)^5 = 24 \cdot \frac{32}{243} \approx 3{,}17$ см
    Ответ: $\frac{24}{81} \cdot 32$ ≈ см или точный ответ, если схема другая. Точное решение требует рисунка.

  12. Если фигура — четырёхугольник с внешними углами, сумма внешних углов любого выпуклого многоугольника равна 360°. Но в задаче отмечены внутренние углы — сумма зависит от типа многоугольника. Если это треугольник, сумма углов 180° и т.д. Точный ответ требует изображения.
  13. Мама купила коробку кускового сахара. Дети сначала съели верхний слой, состоящий из 77 кусочков. Затем они съели передний слой, состоящий из 55 кусочков. Наконец, они съели боковой слой. Сколько кусочков сахара осталось в коробке?
    Решение: Предположим, коробка имеет размеры a × b × c. Тогда:
    Верхний слой: a × b = 77
    Передний слой: a × c = 55
    Боковой слой: b × c Оставшиеся кубики: (a-1)(b-1)(c-1)
    Из уравнений: a,b,c = ? 77=7×11, 55=5×11 ⇒ предположим a=11, b=7, c=5
    Остаток: 10×6×4=240
    Ответ: 240.
  14. Сколько диагоналей у выпуклого \(20\)-угольника?
    Решение: Формула: $\frac{n(n-3)}{2} = \frac{20\cdot17}{2} = 170$.
    Ответ: 170.
  15. Цена билета в театр выросла на \(40\%\), а выручка снизилась на \(16\%\). На сколько процентов уменьшилось число зрителей?
    Решение: Пусть исходная цена p, количество q. Новая цена 1,4p, выручка 0,84pq. Новое количество q' = $\frac{0,84pq}{1,4p} = 0,6q$. Уменьшение на 40%.
    Ответ: 40\%.
  16. Когда пешеход прошёл \(8\) км, из того же пункта вслед за ним выехал велосипедист, скорость которого в \(5\) раз больше скорости пешехода. На каком расстоянии от исходного пункта велосипедист догонит пешехода?
    Решение: Пусть v — скорость пешехода. Время до встречи t:
    $8 + vt = 5v \cdot t$
    $8 = 4vt \Rightarrow t = \frac{8}{4v} = \frac{2}{v}$
    Расстояние от пункта: $5v \cdot \frac{2}{v} = 10$ км
    Ответ: 10 км.
  17. Сколько решений в натуральных числах имеет уравнение \[ a^2b - 1 = 146? \] Решение: $a²b = 147 = 3·7²$. Возможные пары (a, b):
    (1,147), (3,49), (7,3), (21,1)
    Ответ: 4 решения.
  18. Запишем число \[ \frac{1}{5^{146}} \] в виде десятичной дроби. Какова будет последняя цифра?
    Решение: $1/5^{146} = (0.2)^{146} = (2/10)^{146} = 2^{146}/10^{146}$. Последняя цифра числителя:
    2⁴ цикличность: 2,4,8,6. 146 mod 4 = 2 ⇒ последняя цифра 4. Значит, в 146-й позиции после запятой — 4.
    Ответ: 4.
  19. Сколько различных значений может принимать выражение \[ \frac{|a|}{a} + \frac{|b|}{b} + \frac{|ab|}{ab}? \] Решение: Возможные комбинации знаков a и b:
    1) a>0, b>0: 1 + 1 + 1 = 3 2) a>0, b<0: 1 -1 -1 = -1 3) a0: -1 + 1 -1 = -1 4) a<0, b<0: -1 -1 + 1 = -1 Уникальные значения: 3 и -1 ⇒ 2 различных значения.
    Ответ: 2.
  20. Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра, в Петропавловске-Камчатском полдень. Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?
    Решение: Разница Москва-Чикаго: -9 часов. Москва-Петропавловск: +9 часов.
    Когда в Петропавловске 3:00, в Москве 18:00 предыдущего дня.
    В Чикаго: 18:00 - 9 часов = 9:00 утра.
    Ответ: 9 часов утра.
Материалы школы Юайти