МАОУ «СОШ № 146» г.Перми из 6 в 7 класс 2025 год вариант 1

МАОУ "СОШ № 146" г.Перми

2025

Вариант 1

1. Найдите значение выражения: \[ 14 - 13{,}2 \colon \Bigl(3\dfrac{11}{21} - 2\dfrac{4}{15}\Bigr). \]
2. Найдите неизвестный член пропорции \[ \frac{5}{6} \colon 7\dfrac{1}{3} = 1{,}6 \colon x. \]
3. Найдите число \(n\), если \[ \frac{4}{7}n \quad\text{равно}\quad 80% \text{ от } 40. \]
4. Луч \(OM\) разделил угол \(COD\) на два угла \(\angle COM\) и \(\angle MOD\) так, что угол \(COM\) составляет \(\tfrac{2}{3}\) угла \(MOD\). Найдите градусную меру угла \(COD\), если угол \(MOD\) больше угла \(COM\) на \(15^\circ\).
   
   
5. Роман состоит из трёх глав и занимает в книге 340 страниц. Число страниц второй главы составляет \(42\%\) числа страниц первой главы, а число страниц третьей главы составляет \(\tfrac{2}{3}\) числа страниц второй главы. Сколько страниц занимает третья глава романа?
6. Экскурсантов можно посадить в лодки по 8 человек или по 12 человек в каждую. Сколько было экскурсанто, если их больше 80, но меньше 100?
7. Сколько имеется несократимых правильных дробей со знаменателем 115?
   
   
8. Расстояние от пункта \(A\) до пункта \(B\) первый велосипедист проезжает за 8 часов, а второй — за 9 часов. Кто из них проедет больше: первый за 5 часов или второй за 7 часов? В ответе укажите, во сколько раз одно из расстояний больше другого.
   
   
9. Вам нужно заполнить коробку \(8\times5\times3\) кубиками двух типов: \(2\times2\times2\) и \(1\times1\times1\) так, чтобы в коробке не осталось пустого места и было использовано наименьшее количество кубиков. Сколько потребуется кубиков?
10. В автобусе ехали меньше 100 человек, причём число сидящих пассажиров было вдвое больше числа стоящих. На остановке \(4\%\) пассажиров вышли. Сколько пассажиров осталось в автобусе?
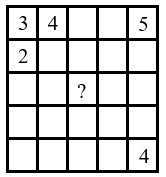
11. Таблицу (см. рис.) нужно заполнить, используя числа 1, 2, 3, 4, 5 так, чтобы каждое число появилось в каждом столбце, каждой строке и каждой диагонали по одному разу. Первые несколько чисел уже расставлены. Какое число будет в центральной клетке?
    
    
    
12. В турнире участвуют 4 футбольные команды. Каждая команда встречается с каждой другой. За победу начисляется 3 очка, за ничью — 1 очко, за поражение — 0 очков. Команды набрали 5, 3, 3 и 2 очка. Сколько было ничьих?
13. Лена и Галя пошли в лес за ягодами. Лена набрала больше 2 кг, но меньше 3 кг, а Галя — больше 3 кг, но меньше 4 кг. По дороге домой они часть ягод съели, Лена — больше, чем 100 г, но меньше, чем 300 г, а Галя — больше, чем 200 г, но меньше, чем 500 г. Дома они взвесили все оставшиеся ягоды вместе. Между какими делениями наверняка остановится стрелка весов? В ответе укажите номер выбранного варианта:
    1. 4,7 и 6,2
    2. 4,2 и 6,2
    3. 4,2 и 6,7
    4. 4,4 и 6,7
    5. не хватает данных
    
    
    
14. Таблица состоит из двух строк, в каждом столбце которой, начиная со второго, записаны сумма и разность предыдущего столбца (всегда из большего числа вычитают меньшее). Найдите сумму чисел первого столбца этой таблицы, если в седьмом столбце стоят числа 96 и 64.
15. Маша выписала все трёхзначные числа от 100 до 999 и подчеркнула те из них, в которых есть хотя бы две одинаковые цифры. Сколько чисел она подчеркнула?
16. Коля и Вася живут в одном доме, на каждом этаже которого расположено 4 квартиры. Коля живёт на 5‑м этаже в квартире № 83, а Вася — на 3‑м этаже в квартире № 169. Сколько этажей в доме?
    
    

Решения задач

1. Найдите значение выражения: \[ 14 - 13,2 \;:\;\Bigl(3\tfrac{11}{21} - 2\tfrac{4}{15}\Bigr). \] Решение: Переведём смешанные числа в неправильные дроби: \[ 3\tfrac{11}{21} = \frac{74}{21}, \quad 2\tfrac{4}{15} = \frac{34}{15}. \] Найдём разность: \[ \frac{74}{21} - \frac{34}{15} = \frac{74 \cdot 5 - 34 \cdot 7}{105} = \frac{132}{105} = \frac{44}{35}. \] Выполним деление: \[ 13,2 : \frac{44}{35} = \frac{66}{5} \cdot \frac{35}{44} = 10,5. \] Итоговый результат: \[ 14 - 10,5 = 3,5. \] Ответ: 3,5.
2. Найдите неизвестный член пропорции \[ \frac{15}{6} : \frac{7}{1,6} = x. \] Решение: Преобразуем пропорцию: \[ x = \frac{15}{6} : \frac{7}{1,6} = \frac{15}{6} \cdot \frac{1,6}{7} = \frac{24}{42} = \frac{4}{7}. \] Ответ: $\frac{4}{7}$.
3. Найдите число $n$, если $\frac{4}{7}$ от $n$ равно $80\%$ от 40. Решение: Найдём число \(n\), если выполняется равенство \[ \frac{4}{7}n = 80. \] Чтобы найти \(n\), умножим обе части на \(\frac{7}{4}\): \[ n = 80 \cdot \frac{7}{4}. \] Сначала вычислим: \[ 80 : 4 = 20. \] Тогда \[ n = 20 \cdot 7 = 140. \] Ответ: \[ 140. \]
4. Луч $OM$ разделил угол $COD$ на два угла $\angle COM$ и $\angle MOD$ так, что угол $COM$ составляет $\tfrac{2}{3}$ угла $MOD$. Найдите градусную меру угла $COD$, если угол $MOD$ больше угла $COM$ на $15^\circ$. Решение: Пусть $\angle MOD = x$, тогда $\angle COM = \frac{2}{3}x$. По условию: \[ x - \frac{2}{3}x = 15 \implies \frac{1}{3}x = 15 \implies x = 45^\circ. \] Угол $COD$ равен: \[ 45^\circ + \frac{2}{3} \cdot 45^\circ = 45^\circ + 30^\circ = 75^\circ. \] Ответ: $75^\circ$.
5. Роман состоит из трёх глав и занимает 340 страниц. Число страниц второй главы составляет $42\%$ первой, третья — $\tfrac{2}{3}$ второй. Сколько страниц занимает третья глава? Решение: Пусть первая глава — $x$ страниц: \[ x + 0,42x + 0,28x = 340 \implies 1,7x = 340 \implies x = 200. \] Третья глава: \[ 0,28 \cdot 200 = 56 \text{ страниц}. \] Ответ: 56.
6. Экскурсантов можно посадить в лодки по 8 или 12 человек. Сколько было экскурсантов, если их больше 80, но меньше 100? Решение: НОК(8, 12) = 24. Число, кратное 24 между 80 и 100: 24 ⋅ 4 = 96. Ответ: 96.
7. Решение. Числитель может быть любым числом от $1$ до $114$, всего $114$ вариантов. Разложим знаменатель: \[ 115 = 5 \cdot 23. \] Дробь будет несократимой, если числитель не делится ни на $5$, ни на $23$. Посчитаем, сколько чисел от $1$ до $114$ делятся на $5$: \[ \left\lfloor \dfrac{114}{5} \right\rfloor = 22. \] Сколько чисел делятся на $23$: \[ \left\lfloor \dfrac{114}{23} \right\rfloor = 4. \] Числа, которые делятся и на $5$, и на $23$, должны делиться на $115$, но таких нет среди чисел до $114$, поэтому просто складываем: \[ 22 + 4 = 26. \] Это количество «плохих» числителей. Тогда «хороших» числителей: \[ 114 - 26 = 88. \] Ответ: $88$ несократимых правильных дробей со знаменателем $115$.
8. Первый велосипедист проезжает путь за 8 часов, второй — за 9. Кто проедет больше за 5 часов и за 7 часов? Решение: Путь первого за 5 часов: \[ \frac{5}{8} \text{ пути}. \] Путь второго за 7 часов: \[ \frac{7}{9} \text{ пути}. \] Сравнение: \[ \frac{7}{9} : \frac{5}{8} = \frac{56}{45} \approx 1,244. \] Ответ: Второй за 7 часов проедет больше в $\frac{56}{45}$ раза.
9. Размер коробки равен \(8 \times 5 \times 3\). Объём коробки: \[ 8 \cdot 5 \cdot 3 = 120. \] Большой кубик имеет размеры \(2 \times 2 \times 2\), его объём: \[ 2 \cdot 2 \cdot 2 = 8. \] Маленький кубик \(1 \times 1 \times 1\) имеет объём \(1\). Чтобы использовать как можно меньше кубиков, нужно взять как можно больше больших кубиков. Рассмотрим внутри коробки прямоугольный блок размера \(8 \times 4 \times 2\). Все его размеры чётные, значит его можно полностью заполнить кубиками \(2 \times 2 \times 2\). По измерению \(8\) можно разместить \(4\) кубика по \(2\), по измерению \(4\) можно разместить \(2\) кубика по \(2\), по измерению \(2\) помещается \(1\) кубик по \(2\). Число больших кубиков в этом блоке: \[ 4 \cdot 2 \cdot 1 = 8. \] После этого остаётся незаполненный объём. Оставшиеся части коробки имеют размеры \(8 \times 1 \times 3\) и \(8 \times 4 \times 1\). В каждом из этих блоков есть измерение, равное \(1\), а большой кубик имеет сторону \(2\), поэтому ни один новый кубик \(2 \times 2 \times 2\) туда не поместится. Значит, \(8\) больших кубиков — это максимальное возможное количество. Объём, занятый большими кубиками: \[ 8 \cdot 8 = 64. \] Оставшийся объём: \[ 120 - 64 = 56. \] Этот объём заполняем маленькими кубиками \(1 \times 1 \times 1\), поэтому маленьких кубиков нужно \(56\). Всего кубиков: \[ 8 + 56 = 64. \] Ответ: 64.
10. В автобусе ехали меньше \(100\) человек, причём сидящих было вдвое больше, чем стоящих. Пусть стоящих было \(x\) человек, тогда сидящих было \(2x\) человек. Всего пассажиров: \[ x + 2x = 3x. \] Значит, общее число пассажиров кратно \(3\). По условию это число меньше \(100\), то есть \[ 3x < 100. \] На остановке вышло \(4\%\) пассажиров. Число вышедших равно \[ 4% \cdot 3x = 0{,}04 \cdot 3x = \frac{3x}{25}, \] и оно должно быть целым числом. Следовательно, \(3x\) делится на \(25\). Итак, общее число пассажиров меньше \(100\), делится на \(3\) и на \(25\). Наименьшее общее кратное чисел \(3\) и \(25\) равно \[ 3 \cdot 25 = 75. \] Число \(75\) меньше \(100\), значит всего было \(75\) пассажиров. Тогда \[ 3x = 75 \Rightarrow x = 25. \] Стоящих было \(25\) человек, сидящих \(2 \cdot 25 = 50\) человек. Теперь найдём, сколько пассажиров вышло: \[ 4% \text{ от } 75 = 0{,}04 \cdot 75 = \frac{75}{25} = 3. \] Осталось в автобусе: \[ 75 - 3 = 72. \] Ответ: 72.
11. Решение.
    В каждой строке, каждом столбце и на каждой диагонали должны стоять числа $1,2,3,4,5$ по одному разу. Значит сумма чисел в любой строке, столбце или диагонали равна \[ 1+2+3+4+5 = 15. \] В первой строке уже стоят числа $3,4,\square,\square,5$. Не хватает чисел $1$ и $2$, поэтому в двух пустых клетках первой строки стоят $1$ и $2$. Рассмотрим диагонали. На главной диагонали уже есть число $3$ (в левом верхнем углу), остальные числа на этой диагонали — это $1,2,4,5$ в каком-то порядке. На другой диагонали уже есть число $5$ (в правом верхнем углу), остальные числа на этой диагонали — это $1,2,3,4$. Значит в центре может стоять только одно из чисел $1,2,4$.
    Пусть в центре стоит $1$. Тогда в первой строке недостающие числа $1$ и $2$ должны стоять так: в третьем столбце не может быть ещё один $1$, потому что в третьем столбце уже стоит $1$ в центре. Значит \[ (1,3)=2,\quad (1,4)=1. \] Посмотрим на вторую диагональ (справа сверху влево вниз). На ней уже стоят числа $5$ (в правом верхнем углу) и $1$ (в центре). Оставшиеся три клетки этой диагонали должны содержать числа $2,3,4$. Нижняя левая клетка таблицы лежит и на этой диагонали, и в первом столбце. В первом столбце уже стоят $3$ и $2$, значит там ещё должны быть числа $1,4,5$. Пересечение возможных чисел по диагонали ($2,3,4$) и по столбцу ($1,4,5$) даёт только число $4$. Значит в нижнем левом углу стоит $4$. Но в нижней строке уже есть число $4$ в четвёртом столбце (дано на рисунке). Получается, в одной строке два раза стоит число $4$, что нельзя. Значит в центре не может стоять $1$. Аналогично при попытке поставить в центр число $2$ при дальнейшем заполнении таблицы снова получается, что в какой-то строке или столбце одно из чисел повторяется. Поэтому число $2$ тоже не подходит. Остаётся единственный возможный вариант для центральной клетки — число $4$. При нём таблицу можно полностью корректно заполнить, например так: \[ \begin{matrix} 3 & 4 & 2 & 1 & 5\\ 2 & 1 & 5 & 3 & 4\\ 5 & 3 & 4 & 2 & 1\\ 4 & 2 & 1 & 5 & 3\\ 1 & 5 & 3 & 4 & 2 \end{matrix} \] В каждой строке, каждом столбце и на обеих диагоналях действительно получаются все числа $1,2,3,4,5$ по одному разу. Итак, в центральной клетке стоит число $4$.
    Ответ:4
12. В турнире участвуют \(4\) команды. Каждая команда сыграла с каждой по одному разу. Всего игр: \[ \binom{4}{2} = 6. \] За победу дают \(3\) очка, за ничью \(1\) очко каждой команде, за поражение \(0\) очков. Если бы {все} \(6\) игр закончились победой одной из команд, то за каждую игру было бы \[ 3 \text{ очка} \] (победителю), итого: \[ 6 \cdot 3 = 18 \text{ очков} \] на весь турнир. На самом деле команды набрали: \[ 5 + 3 + 3 + 2 = 13 \text{ очков}. \] Посмотрим, что делает ничья. Если вместо победы ( \(3\) очка одной команде и \(0\) другой) произошла ничья, то команды получают по \(1\) очку, всего: \[ 1 + 1 = 2 \text{ очка}. \] То есть одна ничья уменьшает общее количество очков на \(1\) (должно было быть \(3\), стало \(2\)). Обозначим количество ничьих через \(k\). Тогда: \[ 18 - k = 13. \] Решаем: \[ 18 - 13 = k, \] \[ k = 5. \] Ответ: 5 $\text{ ничьих}.$
13. Лена набрала больше \(2\) кг, но меньше \(3\) кг, Галя набрала больше \(3\) кг, но меньше \(4\) кг. Сначала всего ягод было: \[ 2 + 3 < \text{всего} < 3 + 4, \] то есть от \(5\) до \(7\) кг, не включая границы. Лена съела больше \(100\) г, но меньше \(300\) г, то есть от \(0{,}1\) до \(0{,}3\) кг. Галя съела больше \(200\) г, но меньше \(500\) г, то есть от \(0{,}2\) до \(0{,}5\) кг. Вместе они съели: \[ 0{,}1 + 0{,}2 < \text{съедено} 5 - 0{,}8 = 4{,}2 \text{ кг}. \] Максимальный остаток получается, когда ягод было как можно больше (чуть меньше \(7\) кг), а съели как можно меньше (чуть больше \(0{,}3\) кг): \[ \text{остаток} < 7 - 0{,}3 = 6{,}7 \text{ кг}. \] Значит, стрелка весов наверняка остановится между делениями \(4{,}2\) и \(6{,}7\). Ответ: промежуток от \(4{,}2\) до \(6{,}7\), это третий вариант.
14. Таблица состоит из двух строк. В каждом новом столбце записывают сумму и разность чисел из предыдущего столбца (из большего вычитают меньшее). В седьмом столбце стоят числа 96 и 64. Нужно найти сумму чисел первого столбца. Заметим, что в каждом столбце:
    • большее число — это сумма двух чисел предыдущего столбца;
    • меньшее число — это разность этих двух чисел.
    То есть если в каком-то столбце стоят числа \(a\) и \(b\), причём \(a > b\), а в предыдущем столбце были числа \(x\) и \(y\), то: \[ a = x + y,\quad b = x - y. \] Сложим и вычтем эти равенства: \[ a + b = 2x,\quad a - b = 2y, \] \[ x = \frac{a + b}{2},\quad y = \frac{a - b}{2}. \] Значит, по двум числам следующего столбца можно найти два числа предыдущего, просто взяв половину суммы и половину разности. Теперь будем идти от седьмого столбца к первому. В седьмом столбце стоят числа 96 и 64. Большее число 96, меньшее 64. Найдём числа шестого столбца: \[ x = \frac{96 + 64}{2} = \frac{160}{2} = 80,\quad y = \frac{96 - 64}{2} = \frac{32}{2} = 16. \] Шестой столбец: \(80\) и \(16\). Повторим шаги для следующих столбцов: Из \((80,16)\): \[ x = \frac{80 + 16}{2} = \frac{96}{2} = 48,\quad y = \frac{80 - 16}{2} = \frac{64}{2} = 32. \] Пятый столбец: \(48\) и \(32\). Из \((48,32)\): \[ x = \frac{48 + 32}{2} = \frac{80}{2} = 40,\quad y = \frac{48 - 32}{2} = \frac{16}{2} = 8. \] Четвёртый столбец: \(40\) и \(8\). Из \((40,8)\): \[ x = \frac{40 + 8}{2} = \frac{48}{2} = 24,\quad y = \frac{40 - 8}{2} = \frac{32}{2} = 16. \] Третий столбец: \(24\) и \(16\). Из \((24,16)\): \[ x = \frac{24 + 16}{2} = \frac{40}{2} = 20,\quad y = \frac{24 - 16}{2} = \frac{8}{2} = 4. \] Второй столбец: \(20\) и \(4\). Из \((20,4)\): \[ x = \frac{20 + 4}{2} = \frac{24}{2} = 12,\quad y = \frac{20 - 4}{2} = \frac{16}{2} = 8. \] Первый столбец: \(12\) и \(8\). Сумма чисел первого столбца: \[ 12 + 8 = 20. \] Ответ: 20.
15. Маша выписала все трёхзначные числа от \(100\) до \(999\) и подчеркнула те, в которых есть хотя бы две одинаковые цифры. Всего трёхзначных чисел: \[ 999 - 100 + 1 = 900. \] Будем считать наоборот: сначала найдём, сколько трёхзначных чисел, у которых \emph{все три цифры разные}, а потом вычтем это число из \(900\). Трёхзначное число имеет вид \(abc\), где \(a\) — сотни, \(b\) — десятки, \(c\) — единицы.
    • Цифра \(a\) (сотни) не может быть нулём. Значит, для \(a\) есть \(9\) вариантов: \[ 1,2,3,4,5,6,7,8,9. \]
    • Цифра \(b\) (десятки) может быть любой цифрой от \(0\) до \(9\), кроме уже выбранной для \(a\). Значит, для \(b\) есть тоже \(9\) вариантов.
    • Цифра \(c\) (единицы) должна отличаться и от \(a\), и от \(b\), то есть нельзя брать две уже использованные цифры. Всего цифр \(10\), две уже заняты, остаётся \(8\) вариантов.
    Тогда количество трёхзначных чисел, у которых все цифры разные: \[ 9 \cdot 9 \cdot 8 = 648. \] Теперь найдём, сколько чисел Маша подчеркнула. Она подчеркнула все, у которых есть хотя бы две одинаковые цифры, то есть не все три цифры разные. Число таких чисел равно \[ 900 - 648 = 252. \] Ответ: 252.
16. В доме несколько подъездов. В каждом подъезде на каждом этаже по $4$ квартиры. Во всех подъездах этажей одинаковое количество.
    Сначала посмотрим на Колю. Он живёт в квартире номер $83$ на $5$-м этаже. В одном подъезде: 1-й этаж: квартиры $1$–$4$ от начала подъезда,
    2-й этаж: квартиры $5$–$8$,
    3-й этаж: квартиры $9$–$12$,
    4-й этаж: квартиры $13$–$16$,
    5-й этаж: квартиры $17$–$20$. Значит, квартира Коли в своём подъезде — это $17$-я, $18$-я, $19$-я или $20$-я квартира от начала подъезда. Посчитаем, сколько квартир было до начала Колиного подъезда: если квартира $83$ — $17$-я, то до подъезда $83-17=66$ квартир;
    если $18$-я, то $83-18=65$;
    если $19$-я, то $83-19=64$;
    если $20$-я, то $83-20=63$. Итак, до Колиного подъезда могло быть $63$, $64$, $65$ или $66$ квартир. До его подъезда стоят только целые подъезды, значит количество квартир до подъезда должно делиться на $4$ (по $4$ квартиры на этаж и одинаковое число этажей). Из чисел $63$, $64$, $65$, $66$ на $4$ делится только $64$. Значит, до подъезда Коли ровно $64$ квартиры. Тогда количество квартир в одном подъезде — делитель числа $64$, не меньше $20$ (в подъезде есть хотя бы $20$ квартир, так как Коля живёт в квартире, которая может быть $20$-й от начала подъезда). Подходящие варианты: $32$ и $64$ квартиры в подъезде.
    Теперь посмотрим на Васю. Он живёт в квартире номер $169$ на $3$-м этаже. В одном подъезде на 3-м этаже находятся квартиры $9$, $10$, $11$, $12$ от начала подъезда. Посчитаем, сколько квартир было до начала Васиного подъезда: если квартира $169$ — $9$-я, то $169-9=160$;
    если $10$-я, то $169-10=159$;
    если $11$-я, то $169-11=158$;
    если $12$-я, то $169-12=157$. То есть до Васиного подъезда могло быть $157$, $158$, $159$ или $160$ квартир. Снова до подъезда стоят только целые подъезды, значит это число тоже делится на $4$. Из этих чисел на $4$ делится только $160$. Значит, до Васиного подъезда $160$ квартир.
    Мы знаем: до Колиного подъезда $64$ квартиры,
    до Васиного подъезда $160$ квартир. Пусть в одном подъезде $64$ квартиры. Тогда $160$ не равно целому числу подъездов по $64$ квартир: $64\cdot 2=128$, $64\cdot 3=192$, а $160$ между ними. Так быть не может. Пусть в одном подъезде $32$ квартиры. Тогда всё хорошо: \[ 64 = 32\cdot 2,\qquad 160 = 32\cdot 5. \] Значит, в одном подъезде $32$ квартиры.
    В одном подъезде $32$ квартиры, на одном этаже $4$ квартиры. Тогда число этажей: \[ 32 : 4 = 8. \] Значит, в подъезде $8$ этажей. Во всех подъездах этажей одинаково, так что и в доме тоже $8$ этажей.
    Ответ: в доме $8$ этажей.