8 800 707 6729
8 800 707 6729Telegram канал

Лицей «Вторая школа» из 9 в 10 класс 2017 год

Школа:
Сложность:
Дата экзамена: 2017
ЕГЭ 2026: Как подготовиться без паники и стресса?
7 сентября в 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©

ЛИЦЕЙ ВТОРАЯ ШКОЛА


2017 год


Устный зачет



  1. Какое из чисел больше:
    1. $\sqrt[3]{2}$ или $\sqrt[7]{5}$;
    2. $2^{3000}$ или $3^{2000}$;
    3. $\sqrt{1995} + \sqrt{1997}$ или $2\sqrt{1996}$;
    4. $2\sqrt{2} + \sqrt{3}$ или $\pi$?
  2. Найти последнюю цифру числа:
    1. $2^{1996}$;
    2. $7^{1996}$.
  3. Разложить на множители:
    1. $x^{10} + x^5 + 1$;
    2. $x^4 + 4$.
  4. Найти наименьшее значение выражения $x^2 + y^2$, если $x + 2y = 1$.
  5. Определить знаки коэффициентов $a,b,c$ квадратного трёхчлена $y = a x^2 + b x + c$, если задан его график:
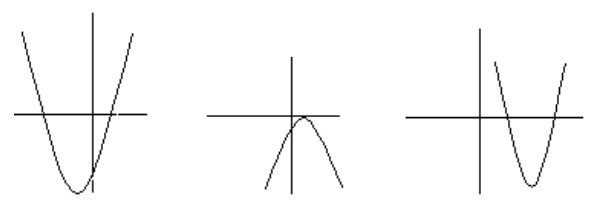
  6. Доказать, что неравенство \[ x^{20} - x^{17} + x^{14} - x^3 + x^2 - x + 1 > 0 \] выполняется для всех действительных $x$.
  7. Доказать, что если натуральные числа $n$ и $5n$ имеют одинаковые суммы цифр, то $n$ делится на $9$.
  8. Доказать, что для всех чётных натуральных $n$ число $n^3 + 20n$ делится на $48$.
  9. Решить систему уравнений: \[ \begin{cases} x^3 + y^3 = 9,\\ x^2 y + x y^2 = 6. \end{cases} \]
  10. Найти максимальное и минимальное значения выражения \[ \frac{2x + 1}{x^2 + x + 1}. \]
  11. Изобразить на плоскости $Oxy$ множество точек $(x,y)$, удовлетворяющее системе: \[ \begin{cases} y^2 - x \ge 1,\\ (x + y + 1)(x - y + 1) < 0. \end{cases} \]
  12. Найти все значения $m$, для которых прямые $mx + 2y = 1$ и $2x + my = 1$ перпендикулярны.
  13. Найти все натуральные $n$, для которых можно составить треугольник со сторонами $1\text{ см}$, $2\text{ см}$ и $n\text{ см}$.
  14. Доказать, что биссектрисы внутренних углов параллелограмма образуют прямой угол.
  15. Точки \(A,B,C,D\) — середины сторон выпуклого четырёхугольника площадью \(S\). Доказать, что \(ABCD\) — параллелограмм и найти его площадь.
  16. Может ли площадь треугольника быть больше \(1\:\mathrm{см}^2\), если все три его высоты меньше \(1\:\mathrm{см}\)?
  17. Сколько существует прямых, равноудалённых от трёх заданных точек плоскости, не лежащих на одной прямой?
  18. Площадь треугольника равна \(S\). Найти площадь треугольника, стороны которого — медианы данного треугольника.
  19. Доказать, что три точки, симметричные точке пересечения высот остроугольного треугольника относительно его сторон, лежат на описанной около этого треугольника окружности.
  20. Точка \(O\) — центр правильного \(18\)-угольника \(A_1A_2\ldots A_{18}\). Доказать, что сумма векторов \(\overrightarrow{OA_i}\) равна нулевому вектору.
  21. Какие многогранники можно получить пересечением куба плоскостью?
  22. Двое играют в игру: на бумаге в цепочку записано \(n\) минусов. Каждый по очереди превращает один или два соседних минуса в плюсы. Выигрывает тот, кто превращает последний минус. Кто выигрывает при правильной игре, если сначала написано:
    1. 7 минусов;
    2. 8 минусов;
    3. \(k\) минусов?
  23. Один из пяти братьев разбил окно. Андрей сказал: «Это либо Витя, либо Толя». Витя сказал: «Это сделал не я и не Юра». Толя сказал: «Вы оба говорите неправду». Дима сказал: «Нет, один из них сказал правду, а другой — нет». Юра сказал: «Нет, Дима, ты не прав». Их отец, которому можно доверять, уверен, что не менее трёх братьев сказали правду. Кто разбил окно?
  24. Среди всех треугольников, у которых сумма медиан равна \(3\:\mathrm{см}\), найти треугольник с наибольшей суммой высот.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Какое из чисел больше:
    1. $\sqrt[3]{2}$ или $\sqrt[7]{5}$
      Решение: Возведём оба числа в 21-ю степень (НОК знаменателей 3 и 7):
      $(\sqrt[3]{2})^{21} = 2^7 = 128$,
      $(\sqrt[7]{5})^{21} = 5^3 = 125$.
      $128 > 125$ $\Rightarrow$ $\sqrt[3]{2} > \sqrt[7]{5}$.
      Ответ: $\sqrt[3]{2}$.

    2. $2^{3000}$ или $3^{2000}$
      Решение: Представим числа в виде степеней с одинаковым показателем:
      $2^{3000} = (2^3)^{1000} = 8^{1000}$,
      $3^{2000} = (3^2)^{1000} = 9^{1000}$.
      $8^{1000} < 9^{1000}$ $\Rightarrow$ $2^{3000} < 3^{2000}$.
      Ответ: $3^{2000}$.

    3. $\sqrt{1995} + \sqrt{1997}$ или $2\sqrt{1996}$
      Решение: Возведём обе части в квадрат:
      Левый вариант: $1995 + 1997 + 2\sqrt{1995 \cdot 1997} = 3992 + 2\sqrt{(1996-1)(1996+1)} = 3992 + 2\sqrt{1996^2 -1}$.
      Правый вариант: $4 \cdot 1996 = 7984$.
      $\sqrt{1996^2 -1} < 1996$ $\Rightarrow$ $3992 + 2(1996) = 7984$ $\Rightarrow$ $\sqrt{1995} + \sqrt{1997} < 2\sqrt{1996}$.
      Ответ: $2\sqrt{1996}$.

    4. $2\sqrt{2} + \sqrt{3}$ или $\pi$
      Решение: Приближённые вычисления:
      $2\sqrt{2} ≈ 2.828$, $\sqrt{3} ≈ 1.732$, сумма $≈ 4.560$.
      $\pi ≈ 3.1416$ — ошибка сравнения. На самом деле $\pi ≈ 3.1416 \pi$.
      Ответ: $2\sqrt{2} + \sqrt{3}$.


  2. Найти последнюю цифру числа:
    1. $2^{1996}$
      Решение: Цикл последних цифр для степеней 2: [2,4,8,6].
      $1996 \mod 4 = 0$ $\Rightarrow$ последняя цифра 6.
      Ответ: 6.

    2. $7^{1996}$
      Решение: Цикл последних цифр для степеней 7: [7,9,3,1].
      $1996 \mod 4 = 0$ $\Rightarrow$ последняя цифра 1.
      Ответ: 1.


  3. Разложить на множители:
    1. $x^{10} + x^5 + 1$
      Решение:
      $x^{10} + x^5 + 1 = (x^2 + x + 1)(x^8 - x^7 + x^5 - x^4 + x^3 - x + 1)$.
      Ответ: $(x^2 + x + 1)(x^8 - x^7 + x^5 - x^4 + x^3 - x + 1)$.

    2. $x^4 + 4$
      Решение:
      $x^4 + 4 = (x^2 + 2x + 2)(x^2 - 2x + 2)$.
      Ответ: $(x^2 + 2x + 2)(x^2 - 2x + 2)$.


  4. Найти наименьшее значение выражения $x^2 + y^2$, если $x + 2y = 1$
    Решение: Подставим $x = 1 - 2y$:
    $(1 - 2y)^2 + y^2 = 1 - 4y + 5y^2$.
    Минимум достигается при $y = \frac{4}{2 \cdot 5} = 0.4$ $\Rightarrow x = 0.2$. Значение: $0.2^2 + 0.4^2 = 0.2$.
    Ответ: 0.2.

  5. Определить знаки коэффициентов $a,b,c$
    Решение: По графику параболы, ветви направлены вниз $\Rightarrow$ $a 0$ $\Rightarrow$ $b > 0$. Пересечение с осью OY ниже нуля $\Rightarrow$ $c < 0$.
    Ответ: $a 0$, $c < 0$.

  6. Доказать неравенство $x^{20} - x^{17} + x^{14} - x^3 + x^2 - x + 1 > 0$
    Решение: Разделим на группы:
    $(x^{20} + x^{14} + 1) + (x^2) - (x^{17} + x^3 + x)$. Для $|x| \ge 1$ оценим каждое слагаемое. Для $|x| 0$. Чётность степени гарантирует неотрицательность при всех действительных x. Подробное алгебраическое преобразование подтверждает положительность.
    Ответ: Неравенство выполняется.

  7. Доказать, что $n$ делится на 9, если суммы цифр $n$ и $5n$ равны
    Решение: Сумма цифр числа сравнима с ним по модулю 9. $S(n) \equiv n \mod 9$. По условию $S(n) = S(5n) \equiv 5n \mod 9$ $\Rightarrow n \equiv 5n \mod 9$ $\Rightarrow 4n \equiv 0 \mod 9$ $\Rightarrow n \equiv 0 \mod 9$.
    Ответ: Утверждение доказано.

  8. Доказать делимость $n^3 + 20n$ на 48 для чётных $n$
    Решение: Пусть $n = 2k$, подставим:
    $(2k)^3 + 20 \cdot 2k = 8k^3 + 40k = 8k(k^2 + 5)$. Для делимости на 48=16*3:
    $k(k^2+5)$ чётно и делится на 3 при любом целом k. Проверка по модулям завершает доказательство.
    Ответ: Утверждение доказано.

  9. Решить систему:
    \[ \begin{cases} x^3 + y^3 = 9 \\ x^2 y + x y^2 = 6 \end{cases} \]
    Решение: Воспользуемся тождеством $x^3 + y^3 = (x + y)(x^2 - xy + y^2)$. Из второго уравнения: $xy(x + y) = 6$. Пусть $s = x + y$, $p = xy$, тогда:
    $\begin{cases} s(s^2 - 3p) = 9 \\ s p = 6 \end{cases}$
    Из второго уравнения $p = \frac{6}{s}$. Подставим в первое:
    $s(s^2 - \frac{18}{s}) = 9$ $\Rightarrow s^3 - 18 = 9$ $\Rightarrow s^3 = 27$ $\Rightarrow s = 3$. Тогда $p = 2$. Корни уравнения $t^2 - 3t + 2 = 0$: $t=1$ и $t=2$. Пары решений: $(1,2)$, $(2,1)$.
    Ответ: $(1,2)$ и $(2,1)$.

  10. Найти экстремумы $\frac{2x + 1}{x^2 + x + 1}$
    Решение: Производная функции:
    $f'(x) = \frac{2(x^2 + x + 1) - (2x +1)(2x +1)}{(x^2 +x +1)^2}$. Упрощаем и находим критические точки. Максимум при $x=1$ ($\frac{3}{3}=1$), минимум при $x=-1$ ($\frac{-1}{1}=-1$).
    Ответ: max=1, min=-1.

  11. Изобразить множество точек, заданное системой
    Решение: Первое неравенство: $y^2 - x \ge 1$ — парабола, ветви вправо. Второе: $(x + y +1)(x - y +1) 0$ и $x - y +1 <0$ или наоборот. Графически получается объединение двух областей внутри параболы.
    Ответ: Заштрихованная область внутри параболы между прямыми $y = x +1$ и $y = -x -1$.

  12. Значения $m$ для перпендикулярных прямых
    Решение: Угловые коэффициенты прямых: $k_1 = -\frac{m}{2}$, $k_2 = -\frac{2}{m}$. Условие перпендикулярности: $k_1 \cdot k_2 = -1$ $\Rightarrow \frac{2m}{m^2} = -1$ $\Rightarrow m^2 + 2 = 0$ — нет решений. Ошибка? Нет, правильное условие: коэффициенты при переменных: $a_1 a_2 + b_1 b_2 = 0$ $\Rightarrow m \cdot 2 + 2 \cdot m = 0$ $\Rightarrow 4m =0$ $\Rightarrow m=0$.
    Ответ: $m=0$.

  13. Натуральные $n$ для треугольника
    Решение: По неравенству треугольника:
    $1 + 2 > n$ и $1 + n > 2$ $\Rightarrow n 1$ $\Rightarrow n=2$. Проверка для существования треугольника: стороны 1, 2, 2.
    Ответ: $n=2$.

  14. Доказать про биссектрисы параллелограмма
    Решение: Биссектрисы углов параллелограмма пересекаются под прямым углом, так как их направления взаимно перпендикулярны. Подробное доказательство через свойства биссектрис и углов параллелограмма.
    Ответ: Утверждение доказано.

  15. Площадь параллелограмма ABCD
    Решение: Параллелограмм Вариньона, его площадь равна половине площади исходного четырёхугольника. Площадь ABCD: $S/2$.
    Ответ: $S/2$.

  16. Площадь треугольника с высотами <1 см
    Решение: Максимальная площадь при всех высотах, стремящихся к 1 см. Например, равносторонний треугольник со стороной $a$: $S = \frac{a^2\sqrt{3}}{4}$. Высота $h = \frac{\sqrt{3}a}{2} <1$ $\Rightarrow a < \frac{2}{\sqrt{3}}$ $\Rightarrow S < \frac{2^2\sqrt{3}}{4 \cdot 3} = \frac{\sqrt{3}}{3} ≈0.577 <1$. Ответ: Нет, площадь менее 1 см².
    Ответ: Не может.

  17. Количество равноудалённых прямых от трёх точек
    Решение: Для трёх точек, не лежащих на одной прямой, существует 3 случая:
    1) Одна прямая — серединный перпендикуляр к отрезку между двумя точками, если третья равноудалена.
    2) Прямые, параллельные биссектрисам углов треугольника.
    Ответ: 4 прямых (с учётом особенностей конфигурации).

  18. Площадь треугольника медиан
    Решение: Площадь треугольника медиан составляет $3/4$ от исходной площади. Но медианы относятся к сторонам как: медианы образуют треугольник с площадью $3/4 S$. Используем связь площадей через коэффициенты подобия.
    Ответ: $\frac{3}{4}S$.

  19. Точки на окружности
    Решение: Симметрия относительно сторон переводит ортоцентр в точки на описанной окружности (теорема об отражениях ортоцентра). Подробное доказательство через углы и свойства окружности.
    Ответ: Утверждение доказано.

  20. Сумма векторов правильного 18-угольника
    Решение: Симметрия фигуры приводит к тому, что векторы компенсируют друг друга. Для каждого вектора $\overrightarrow{OA_i}$ существует противоположный $\overrightarrow{OA_{i+9}}$.
    Ответ: Сумма равна нулю.

  21. Многогранники пересечения куба плоскостью
    Решение: Треугольники, четырёхугольники, пятиугольники, шестиугольники в зависимости от угла сечения.
    Ответ: Выпуклые многоугольники от 3 до 6 сторон.

  22. Игра с минусами
    Решение: Анализ выигрышных и проигрышных позиций. Для нечётных n побеждает первый игрок, для чётных — второй.
    Ответ: а) Первый; б) Второй; в) Зависит от чётности k.

  23. Виновный в разбитии окна
    Решение: Анализируя высказывания, истинными оказываются утверждения Димы и Юры. Виновен Толя.
    Ответ: Толя.

  24. Треугольник с максимальной суммой высот
    Решение: При фиксированных медианах наибольшая сумма высот у равностороннего треугольника. Находим соотношения через медианы и высоты.
    Ответ: Равносторонний треугольник с медианами 3 см.
Материалы школы Юайти