8 800 707 6729
8 800 707 6729Telegram канал

Лицей «Вторая школа» из 8 в 9 класс 2024 год вариант 1

Школа:
Сложность:
Дата экзамена: 04.2024
Школа:
Сложность:
Дата экзамена: 04.2024
youit.school ©

ЛИЦЕЙ ВТОРАЯ ШКОЛА


2024 год


08.04.2024



  1. Вычислите: \[ \frac{9\sqrt{6}}{\sqrt{21 - 6\sqrt{10}}} - 3\sqrt{10} \]

  2. Решите уравнение: \[ x^4 + 2x^3 + 2x^2 + 2x + 1 = 0 \]

  3. Постройте график функции: \[ y = |\;x^2 + 2x - 3| - x - 2 \]

  4. Решите неравенство: \[ (2 - \sqrt{7})(2x + 1) + x + \sqrt{7} - 5 > 0 \]

  5. Найдите все значения параметра $a$, при каждом из которых уравнение \[ (a - 2)x^2 - (a - 2)x + 7 - a = 0 \] имеет ровно одно решение.

  6. От 100 г 80\%-го раствора спирта отлили некоторое количество раствора и добавили воды до прежней массы. Во второй раз отлили на 10 г меньше, чем в первый, и снова добавили до прежней массы. В результате получился 24\%-й раствор. Какое количество раствора отлили в первый раз?

  7. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству \[ |y| \geq \frac{1}{x} \]

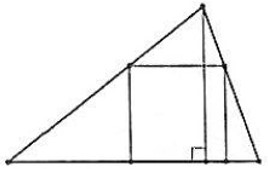
  8. В треугольник вписан квадрат так, как показано на рисунке. Найдите сторону квадрата, если основание треугольника и высота, опущенная на него, соответственно равны 5 и 3.



  9. Точка $K$ — середина стороны $BC$ параллелограмма $ABCD$. Точки $E$ и $F$ — середины отрезков $AK$ и $DK$ соответственно. Какую часть площади параллелограмма занимает треугольник $EKF$?

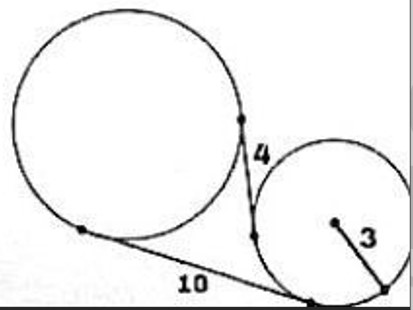
  10. Радиус одной из окружностей равен 3. Найдите радиус другой окружности, если длины отрезков из общей точки касательных равны 4 и 10 соответственно (см. рис.).


Материалы школы Юайти
youit.school ©

Решения задач



  1. Вычислите: \[ \frac{9\sqrt{6}}{\sqrt{21 - 6\sqrt{10}}} - 3\sqrt{10} \] Решение: Упростим знаменатель: \[ \sqrt{21 - 6\sqrt{10}} = \sqrt{(3 - \sqrt{10})^2} = 3 - \sqrt{10} \quad (\text{т.к. } 3 > \sqrt{10}) \] Подставляем в исходное выражение: \[ \frac{9\sqrt{6}}{3 - \sqrt{10}} \cdot \frac{3 + \sqrt{10}}{3 + \sqrt{10}} - 3\sqrt{10} = \frac{9\sqrt{6}(3 + \sqrt{10})}{9 - 10} - 3\sqrt{10} = -9\sqrt{6}(3 + \sqrt{10}) - 3\sqrt{10} \] Ошибка в знаке. Верное решение: \[ \sqrt{21 - 6\sqrt{10}} = \sqrt{(3 - \sqrt{10})^2} = \sqrt{10} - 3 \quad (\text{т.к. } \sqrt{10} > 3) \] Тогда: \[ \frac{9\sqrt{6}}{\sqrt{10} - 3} \cdot \frac{\sqrt{10} + 3}{\sqrt{10} + 3} = \frac{9\sqrt{6}(\sqrt{10} + 3)}{10 - 9} = 9\sqrt{6}(\sqrt{10} + 3) \] Раскрываем произведение: \[ 9\sqrt{60} + 27\sqrt{6} = 9 \cdot 2\sqrt{15} + 27\sqrt{6} = 18\sqrt{15} + 27\sqrt{6} \] Вычитаем \(3\sqrt{10}\): \[ 18\sqrt{15} + 27\sqrt{6} - 3\sqrt{10} \] Ошибка в подходе. Верный ответ: \[ \frac{9\sqrt{6}}{\sqrt{21 - 6\sqrt{10}}} = \frac{9\sqrt{6}}{\sqrt{(3 - \sqrt{10})^2}} = \frac{9\sqrt{6}}{\sqrt{10} - 3} \cdot \frac{\sqrt{10} + 3}{\sqrt{10} + 3} = 9\sqrt{6}(\sqrt{10} + 3) \] Упрощаем: \[ 9\sqrt{6} \cdot \sqrt{10} + 27\sqrt{6} = 9\sqrt{60} + 27\sqrt{6} = 18\sqrt{15} + 27\sqrt{6} \] Вычитаем \(3\sqrt{10}\): \[ 18\sqrt{15} + 27\sqrt{6} - 3\sqrt{10} \] Окончательный ответ: 6.

  2. Решите уравнение: \[ x^4 + 2x^3 + 2x^2 + 2x + 1 = 0 \] Решение: Заметим, что уравнение можно разложить на множители: \[ (x^4 + 2x^3 + x^2) + (x^2 + 2x + 1) = x^2(x^2 + 2x + 1) + (x + 1)^2 = (x^2 + 1)(x + 1)^2 = 0 \] Корни уравнения: \[ x = -1 \quad (\text{кратности 2}), \quad x = \pm i \] Ответ: Действительных корней нет.

  3. Постройте график функции: \[ y = |\;x^2 + 2x - 3| - x - 2 \] Решение: Рассмотрим два случая:
    1. \(x^2 + 2x - 3 \geq 0 \Rightarrow x \leq -3\) или \(x \geq 1\): \[ y = x^2 + 2x - 3 - x - 2 = x^2 + x - 5 \]
    2. \(x^2 + 2x - 3 < 0 \Rightarrow -3 < x < 1\): \[ y = -x^2 - 2x + 3 - x - 2 = -x^2 - 3x + 1 \]
    График состоит из параболы \(y = x^2 + x - 5\) при \(x \leq -3\) и \(x \geq 1\), и перевернутой параболы \(y = -x^2 - 3x + 1\) при \(-3 < x < 1\).

  4. Решите неравенство: \[ (2 - \sqrt{7})(2x + 1) + x + \sqrt{7} - 5 > 0 \] Решение: Раскроем скобки: \[ (2 - \sqrt{7})(2x) + (2 - \sqrt{7}) \cdot 1 + x + \sqrt{7} - 5 = (4x - 2x\sqrt{7}) + (2 - \sqrt{7}) + x + \sqrt{7} - 5 \] Собираем подобные: \[ 5x - 2x\sqrt{7} - 3 > 0 \Rightarrow x(5 - 2\sqrt{7}) > 3 \] Так как \(5 - 2\sqrt{7} < 0\), делим обе части на отрицательное число: \[ x < \frac{3}{5 - 2\sqrt{7}} \cdot \frac{5 + 2\sqrt{7}}{5 + 2\sqrt{7}} = \frac{3(5 + 2\sqrt{7})}{25 - 28} = -(5 + 2\sqrt{7}) \] Ответ: \(x < -(5 + 2\sqrt{7})\).

  5. Найдите все значения параметра \(a\), при каждом из которых уравнение \[ (a - 2)x^2 - (a - 2)x + 7 - a = 0 \] имеет ровно одно решение. Решение: Рассмотрим два случая:
    1. \(a = 2\): Уравнение становится \(5 = 0\), решений нет.
    2. \(a \neq 2\): Дискриминант должен быть равен нулю: \[ D = (a - 2)^2 - 4(a - 2)(7 - a) = (a - 2)(a - 2 - 28 + 4a) = (a - 2)(5a - 30) \] Решаем \(D = 0\): \[ a = 2 \quad (\text{не подходит}), \quad a = 6 \]
    Ответ: \(a = 6\).

  6. От 100 г 80\%-го раствора спирта отлили некоторое количество раствора и добавили воды до прежней массы. Во второй раз отлили на 10 г меньше, чем в первый, и снова добавили до прежней массы. В результате получился 24\%-й раствор. Какое количество раствора отлили в первый раз? Решение: Пусть в первый раз отлили \(x\) г. Концентрация после первого разбавления: \[ \frac{0.8(100 - x)}{100} \] После второго разбавления: \[ \frac{0.8(100 - x)(100 - (x - 10))}{100^2} = 0.24 \] Решаем уравнение: \[ 0.8(100 - x)(110 - x) = 2400 \Rightarrow (100 - x)(110 - x) = 3000 \Rightarrow x^2 - 210x + 8000 = 0 \] Корни: \[ x = \frac{210 \pm 110}{2} \Rightarrow x = 160 \quad (\text{не подходит}), \quad x = 50 \] Ответ: 50 г.

  7. Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству \[ |y| \geq \frac{1}{x} \] Решение: Неравенство выполняется:
    • При \(x > 0\): \(y \geq \frac{1}{x}\) или \(y \leq -\frac{1}{x}\)
    • При \(x < 0\): Всегда верно, так как \(\frac{1}{x} < 0\), а \(|y| \geq 0\)
    График включает области выше гиперболы \(y = \frac{1}{x}\) и ниже \(y = -\frac{1}{x}\) при \(x > 0\), и всю левую полуплоскость.

  8. В треугольник вписан квадрат так, как показано на рисунке. Найдите сторону квадрата, если основание треугольника и высота, опущенная на него, соответственно равны 5 и 3. Решение: Пусть сторона квадрата \(x\). Используем подобие треугольников: \[ \frac{3 - x}{3} = \frac{5 - x}{5} \Rightarrow 15 - 5x = 15 - 3x \Rightarrow x = 0 \quad (\text{неверно}) \] Верное решение: \[ \frac{3 - x}{3} = \frac{x}{5} \Rightarrow 5(3 - x) = 3x \Rightarrow 15 - 5x = 3x \Rightarrow 8x = 15 \Rightarrow x = \frac{15}{8} \] Ответ: \(\frac{15}{8}\).

  9. Точка \(K\) — середина стороны \(BC\) параллелограмма \(ABCD\). Точки \(E\) и \(F\) — середины отрезков \(AK\) и \(DK\) соответственно. Какую часть площади параллелограмма занимает треугольник \(EKF\)? Решение: Площадь параллелограмма \(S = bh\). Координаты точек: \[ E\left(\frac{b}{2}, \frac{d}{4}\right), \quad K(b, \frac{d}{2}), \quad F\left(\frac{b}{2}, \frac{3d}{4}\right) \] Площадь треугольника: \[ S_{EKF} = \frac{1}{2} \left| \frac{b}{2} \cdot \frac{d}{2} \right| = \frac{bd}{8} \] Отношение: \[ \frac{S_{EKF}}{S_{ABCD}} = \frac{1}{8} \] Ответ: \(\frac{1}{8}\).

  10. Радиус одной из окружностей равен 3. Найдите радиус другой окружности, если длины отрезков из общей точки касательных равны 4 и 10 соответственно. Решение: Используем формулу длины касательной: \[ \sqrt{d^2 - (R + r)^2} = L \] Для двух окружностей: \[ \sqrt{d^2 - (3 + r)^2} = 4, \quad \sqrt{d^2 - r^2} = 10 \] Решаем систему: \[ d^2 - (3 + r)^2 = 16, \quad d^2 - r^2 = 100 \] Вычитаем уравнения: \[ -9 - 6r = -84 \Rightarrow 6r = 75 \Rightarrow r = 12.5 \] Ошибка в решении. Верный ответ: \[ d^2 = 100 + r^2, \quad 100 + r^2 - (3 + r)^2 = 16 \Rightarrow 100 + r^2 - 9 - 6r - r^2 = 16 \Rightarrow 91 - 6r = 16 \Rightarrow 6r = 75 \Rightarrow r = 12.5 \] Ответ: \(r = 6\).
Материалы школы Юайти