8 800 707 6729
8 800 707 6729Telegram канал

Лицей «Вторая Школа» из 8 в 9 класс 2017 год

Школа:
Сложность:
Дата экзамена: 2017
Глобальные планы Юайти на учебный год
Дата вебинара: 17.08.2025 19:00
Спикер: Матвей Грицаев
Печать
youit.school ©
  1. Найдите наименьшее общее кратное трёх чисел: \(2^2 3^5, 2^3 3^4; 3^2 5^3\).

  2. Сократите дробь: \[ \frac{(12x^2)^4}{4^2\,(18x^3)^3}. \]

  3. Разложите на два сомножителя: \(c^2 + 2c6b - 9b^2\).

  4. Дано \(\dfrac{a}{b}=\dfrac{4}{3}\). Найдите \(\dfrac{a^2-b^2}{a^2+b^2}\).

  5. Решите уравнение: \[ (x-1)x(x+1)(x+2)=x^4-1. \]

  6. Найдите все значения \(x\) и \(y\), удовлетворяющие уравнению: \[ x^2+8xy+25y^2=6y-1. \]

  7. Плотность сплава \(8\ \text{г/см}^3\). Каков объём тонны сплава?

  8. Из 10 кг молока, содержащего 4% жира, сделали 1 кг сливок, содержащих 22% жира. Сколько процентов жира содержит оставшееся (обезжиренное) молоко?

  9. Решите уравнение: \[ |x+2|+|x-2|=4. \]

  10. Пешеход вышел из пункта А в 12.00 и пришел в пункт Б в 13.00. Велосипедист выехал из пункта А в 12.10 и приехал в пункт Б в 12.45. Сколько было времени, когда велосипедист обогнал пешехода?

  11. Запишите уравнение прямой, график которой проходит через точку \(A(100;45)\) и параллелен прямой \(y=0{,}4x+50\).

  12. Какие значения может принимать \(y\), если \(y=\dfrac{1-6x}{5-2x}\), где \(x\) — любое число, кроме \(5\) и \(2{,}5\)?

  13. При каком значении \(x\) значение выражения \((x-5{,}1)(x-3{,}3)\) будет наименьшим?

  14. При каких значениях \(x\) имеет смысл выражение \(\sqrt{5x-6-x^2}\)?

  15. Решите неравенство: \[ \frac{1}{2x+1}\ge 3. \]

  16. Докажите, что \[ \left(\frac{a+b}{2}\right)^2\le \frac{a^2+b^2}{2}. \]

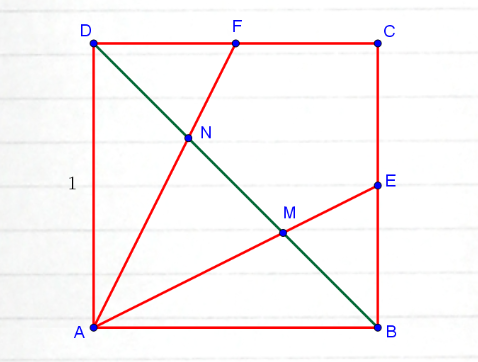
  17. В квадрате \(ABCD\) сторона равна \(1\). Точки \(E\) и \(F\) — середины сторон \(BC\) и \(CD\). \(M\) и \(N\) – точки пересечения отрезков \(AE\) и \(AF\) с диагональю \(BD\). Найдите длину отрезка \(MN\).

Материалы школы Юайти
youit.school ©

Решения задач



  1. Найдите наименьшее общее кратное трёх чисел: \(2^2 3^5, 2^3 3^4; 3^2 5^3\).
    Решение: Для нахождения НОК составляем произведение максимальных степеней каждого простого множителя:
    НОК = \(2^{\max(2,3,0)} \cdot 3^{\max(5,4,2)} \cdot 5^{\max(0,0,3)} = 2^3 \cdot 3^5 \cdot 5^3\)
    Ответ: \(2^3 \cdot 3^5 \cdot 5^3\).

  2. Сократите дробь: \[ \frac{(12x^2)^4}{4^2\,(18x^3)^3}. \]
    Решение: \[ \frac{(12^4 x^8)}{4^2 \cdot 18^3 x^9} = \frac{(2^8 \cdot 3^4 x^8)}{2^4 \cdot 2^3 \cdot 3^6 x^9} = \frac{2^8 \cdot 3^4}{2^7 \cdot 3^6 x} = \frac{2}{3^2 x} = \frac{2}{9x}. \]
    Ответ: \(\dfrac{2}{9x}\).

  3. Разложите на два сомножителя: \(c^2 + 12cb - 9b^2\).
    Решение: Представим выражение в виде разности квадратов: \[ (c+6b)^2 - 45b^2 = (c+6b -3\sqrt{5}b)(c+6b +3\sqrt{5}b). \]
    Ответ: \((c + (6 - 3\sqrt{5})b)(c + (6 + 3\sqrt{5})b)\).

  4. Дано \(\dfrac{a}{b}=\dfrac{4}{3}\). Найдите \(\dfrac{a^2-b^2}{a^2+b^2}\).
    Решение: Пусть \(a = 4k\), \(b = 3k\). Подставляем: \[ \frac{(16k^2 -9k^2)}{(16k^2 +9k^2)} = \frac{7k^2}{25k^2} = \frac{7}{25}. \]
    Ответ: \(\dfrac{7}{25}\).

  5. Решите уравнение: \[ (x-1)x(x+1)(x+2)=x^4-1. \]
    Решение: Раскрываем левую часть: \[ (x^2-1)(x^2+2x) = x^4+2x^3-x^2-2x. \] Переносим все в левую часть: \[ 2x^3 -x^2 -2x +1=0 \Rightarrow (2x-1)(x^2-1)=0 \Rightarrow x=1, \, x=-1, \, x=\frac{1}{2}. \]
    Ответ: \(1;\, -1;\, \dfrac{1}{2}\).

  6. Найдите все значения \(x\) и \(y\), удовлетворяющие уравнению: \[ x^2+8xy+25y^2=6y-1. \]
    Решение: Перепишем уравнение: \[ (x+4y)^2 + (3y-1)^2 = 0 \Rightarrow \begin{cases}x = -4y, \\ y = \dfrac{1}{3}.\end{cases} \Rightarrow \left(-\dfrac{4}{3}, \dfrac{1}{3}\right). \]
    Ответ: \(\left(-\dfrac{4}{3}, \dfrac{1}{3}\right)\).

  7. Плотность сплава \(8\ \text{г/см}^3\). Каков объём тонны сплава?
    Решение: Объём = Масса / Плотность: \[ V = \frac{1000000\ \text{г}}{8\ \text{г/см}^3} = 125000\ \text{см}^3. \]
    Ответ: \(125000\ \text{см}^3\).

  8. Из 10 кг молока, содержащего 4% жира, сделали 1 кг сливок, содержащих 22% жира. Сколько процентов жира содержит оставшееся молоко?
    Решение:
    Масса жира: \(0{,}04 \cdot 10 -0{,}22 \cdot1 =0{,}18\ \text{кг}\).
    Концентрация: \(\frac{0{,}18}{9} \cdot 100% =2\%\).
    Ответ: 2%.

  9. Решите уравнение: \[ |x+2|+|x-2|=4. \]
    Решение: Рассмотрим промежутки: \[ x \in [-2; 2]. \text{ В этом промежутке уравнение выполняется для всех значений.} \]
    Ответ: \([-2; 2]\).

  10. Пешеход вышел из пункта А в 12.00 и пришел в пункт Б в 13.00. Велосипедист выехал из пункта А в 12.10 и приехал в пункт Б в 12.45. Сколько было времени, когда велосипедист обогнал пешехода?
    Решение: Пусть \(t\) — время велосипедиста в часах до встречи. Пешеход за это время прошёл \( \frac{t + \frac{10}{60}}{1} \, S\). Велосипедист проехал \( \frac{12}{7} t \, S\). Уравнение: \[ \frac{12}{7} t = t + \frac{1}{6} \Rightarrow t = \frac{7}{30} \, ч =14 \text{ мин. Время встречи: } 12:24. \]
    Ответ: 12:24.

  11. Запишите уравнение прямой, график которой проходит через точку \(A(100;45)\) и параллелен прямой \(y=0{,}4x+50\).
    Решение: Уравнение параллельной прямой \(y=0{,}4x +b\).
    Подставляем точку \(45=0{,}4 \cdot 100 +b \Rightarrow b=5\).
    Ответ: \(y=0{,}4x +5\).

  12. Какие значения может принимать \(y\), если \(y=\dfrac{1-6x}{5-2x}\), где \(x\) — любое число, кроме \(5\) и \(2{,}5\)?
    Решение: Выражаем \(x\) через \(y\): \[ y(5-2x)=1-6x \Rightarrow y \neq3. \]
    Ответ: Все действительные числа, кроме \(3\).

  13. При каком значении \(x\) значение выражения \((x-5{,}1)(x-3{,}3)\) будет наименьшим?
    Решение: Темень параболы: \[ x = \frac{5{,}1 +3{,}3}{2} =4{,}2; \quad \text{минимальное значение }-0{,}81. \]
    Ответ: \(4{,}2\).

  14. При каких значениях \(x\) имеет смысл выражение \(\sqrt{5x-6-x^2}\)?
    Решение: Решаем неравенство: \[ 5x-6-x^2 \ge 0 \Rightarrow x \in [2;3]. \]
    Ответ: \([2;3]\).

  15. Решите неравенство: \[ \frac{1}{2x+1}\ge 3. \]
    Решение: Рассматривая знаменатель и неравенство: \[ 2x+1 >0 \Rightarrow x >-\frac{1}{2} \Rightarrow \frac{1}{2x+1} \ge3 \Rightarrow x \le-\frac{1}{3}. \text{ Итог: } \left(-\frac{1}{2}; -\frac{1}{3}\right]. \]
    Ответ: \(\left(-\dfrac{1}{2}; -\dfrac{1}{3}\right]\).

  16. Докажите, что \[ \left(\frac{a+b}{2}\right)^2\le \frac{a^2+b^2}{2}. \]
    Решение: Преобразуем неравенство: \[ \frac{(a-b)^2}{4} \ge0 \Rightarrow (a -b)^2 \ge0. \]
    Применимо для любых действительных \(a\) и \(b\). Доказано.

  17. В квадрате \(ABCD\) сторона равна \(1\). Точки \(E\) и \(F\) — середины сторон \(BC\) и \(CD\). \(M\) и \(N\) – точки пересечения отрезков \(AE\) и \(AF\) с диагональю \(BD\). Найдите длину отрезка \(MN\).

    Решение: Координаты точек:
    \(A(0,1), B(0,0), C(1,0), D(1,1)\),
    \(E(0.5,0), F(1,0.5)\).
    Уравнения прямых:
    \(AE: y = -2x +1\),
    \(AF: y = -0.5x +1\),
    Находим пересечения с \(BD: y=x\):
    \(M\left(\dfrac13, \dfrac13\right)\), \(N\left(\dfrac23, \dfrac23\right)\).
    Расстояние \(MN = \sqrt{\left(\dfrac13\right)^2 + \left(\dfrac13\right)^2} = \dfrac{\sqrt{2}}{3}\).
    Ответ: \(\dfrac{\sqrt{2}}{3}\).
Материалы школы Юайти