Лицей «Вторая школа» из 7 в 8 класс 2020 год билет 8

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2020 год

Билет 8

Вопрос 11.

• Параллельные прямые и секущая.
• Углы, образованные при пересечении параллельных прямых секущей (соответственные, накрест лежащие, односторонние).

Вопрос 12.

• Теорема о сумме углов треугольника.
• Внешний угол треугольника и его свойства.

Задачи:

1. На сторонах \(AB\) и \(BC\) треугольника \(ABC\) взяли точки \(M\) и \(K\). Отрезки \(AK\) и \(CM\) пересекаются в точке \(O\). Оказалось, что \(AO = CO\), \(MO = KO\). Докажите, что треугольник \(ABC\) равнобедренный.
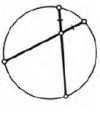
2. Две хорды пересекаются так, что отмеченные на рисунке отрезки равны. Докажите, что сами хорды тоже равны.
   

Решения задач

1. На сторонах \(AB\) и \(BC\) треугольника \(ABC\) взяли точки \(M\) и \(K\). Отрезки \(AK\) и \(CM\) пересекаются в точке \(O\). Оказалось, что \(AO = CO\), \(MO = KO\). Докажите, что треугольник \(ABC\) равнобедренный.
   Решение:
   1. Рассмотрим треугольники \(AMO\) и \(CKO\):
   - \(AO = CO\) (по условию)
   - \(MO = KO\) (по условию)
   - \(\angle AOM = \angle COK\) (вертикальные углы)
   Следовательно, \(\triangle AMO \cong \triangle CKO\) по первому признаку равенства треугольников (по двум сторонам и углу между ними).
   2. Из равенства треугольников следует:
   - \(AM = CK\)
   - \(\angle OAM = \angle OCK\)
   3. Рассмотрим треугольники \(AOK\) и \(COM\):
   - \(AO = CO\) (по условию)
   - \(OK = OM\) (по условию \(MO = KO\))
   - \(\angle AOK = \angle COM\) (вертикальные углы)
   Следовательно, \(\triangle AOK \cong \triangle COM\) по первому признаку равенства.
   4. Из равенства треугольников следует:
   - \(AK = CM\)
   - \(\angle OAK = \angle OCM\)
   5. Из пунктов 2 и 4 получаем, что \(\angle BAC = \angle BCA\), так как:
   \(\angle BAC = \angle OAM + \angle OAK\)
   \(\angle BCA = \angle OCK + \angle OCM\)
   Все соответствующие углы равны.
   6. Таким образом, треугольник \(ABC\) — равнобедренный с основанием \(AC\) (по признаку равнобедренного треугольника: если углы при основании равны, то треугольник равнобедренный).
   Ответ: треугольник \(ABC\) равнобедренный.
   
   
2. Две хорды пересекаются так, что отмеченные на рисунке отрезки равны. Докажите, что сами хорды тоже равны.
   Решение:
   1. Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(O\), причем \(AO = OD\) и \(BO = OC\) (по условию равенства отмеченных отрезков).
   2. По теореме о пересекающихся хордах:
   \(AO \cdot OB = CO \cdot OD\)
   3. Подставим равенства из условия:
   \(AO \cdot BO = BO \cdot AO\) (так как \(CO = BO\) и \(OD = AO\))
   Уравнение выполняется тождественно.
   4. Длина хорды \(AB\) равна:
   \(AB = AO + OB = AO + BO\)
   5. Длина хорды \(CD\) равна:
   \(CD = CO + OD = BO + AO = AO + BO\)
   6. Следовательно, \(AB = CD\), что и требовалось доказать.
   Ответ: хорды равны.