Лицей «Вторая школа» из 7 в 8 класс 2020 год билет 7

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2020 год

Билет 7

Вопрос 7.

• Построение треугольника по трём сторонам.
• Построение треугольника по стороне и двум прилежащим углам.
• Построение треугольника по стороне, прилежащему углу и противолежащей стороне.

Вопрос 18.

• Вписанная окружность треугольника (определение).
• Центр вписанной окружности.
• Свойства вписанной окружности.

Задачи:

1. Один из углов треугольника в два раза больше другого. Высота, опущенная из третьего угла, делит сторону на два отрезка. Докажите, что разность этих отрезков равна одной из сторон треугольника.
   
   
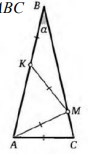
2. На боковых сторонах \(AB\) и \(BC\) равнобедренного треугольника \(ABC\) взяли точки \(M\) и \(K\) соответственно так, что \(BK = KM = AM = AC\). Найдите угол треугольника, противоположный основанию.
   

Решения задач

1. Вопрос 7. Построение треугольников:
   • По трём сторонам: Для построения треугольника по трём сторонам $a$, $b$, $c$ необходимо, чтобы выполнялось неравенство треугольника: сумма любых двух сторон должна быть больше третьей. Алгоритм построения:
     1. Провести прямую линию и отложить на ней сторону $a$ (например, $AB$).
     2. Из точки $A$ провести дугу окружности радиусом $b$.
     3. Из точки $B$ провести дугу окружности радиусом $c$. \
     4. Точка пересечения дуг ($C$) будет третьей вершиной треугольника.
   • По стороне и двум прилежащим углам: Пусть дана сторона $AB$ и углы $\alpha$ и $\beta$ при вершинах $A$ и $B$ соответственно. Условие построения: $\alpha + \beta < 180^\circ$. Алгоритм:
     1. Отложить отрезок $AB$.
     2. Построить угол $\alpha$ при вершине $A$.
     3. Построить угол $\beta$ при вершине $B$.
     4. Точка пересечения сторон углов ($C$) будет третьей вершиной треугольника.
   • По стороне, прилежащему углу и противолежащей стороне: Пусть даны сторона $AB = c$, угол $\alpha$ при вершине $A$ и противолежащая сторона $BC = a$. Алгоритм:
     1. Отложить отрезок $AB = c$.
     2. Построить угол $\alpha$ при вершине $A$.
     3. На стороне угла отложить дугу радиусом $a$ с центром в точке $B$.
     4. Точка пересечения дуги со стороной угла ($C$) будет третьей вершиной треугольника.
2. Вопрос 18. Вписанная окружность:
   • Определение: Окружность, касающаяся всех трёх сторон треугольника, называется вписанной.
   • Центр: Точка пересечения биссектрис углов треугольника.
   • Свойства:
     1. Радиус вписанной окружности ($r$) связан с площадью ($S$) и полупериметром ($p$) треугольника: $r = \frac{S}{p}$.
     2. Центр вписанной окружности равноудалён от всех сторон треугольника.
     3. Точки касания делят стороны на отрезки, равные $p - a$, $p - b$, $p - c$, где $a$, $b$, $c$ — стороны треугольника.
3. Задача 1. Пусть в треугольнике $ABC$ $\angle A = 2\angle B$, высота $CH$ делит $AB$ на отрезки $AH$ и $HB$. Доказать: $|AH - HB| = AC$ или $BC$.
   Решение:
   1. Обозначим $\angle B = x$, тогда $\angle A = 2x$, $\angle C = 180^\circ - 3x$.
   2. Выразим стороны через теорему синусов: $\frac{AC}{\sin x} = \frac{BC}{\sin 2x} = \frac{AB}{\sin(180^\circ - 3x)} = \frac{AB}{\sin 3x}$.
   3. Рассмотрим прямоугольные треугольники $ACH$ и $BCH$:
      • $AH = AC \cos(2x)$,
      • $HB = BC \cos x$.
   4. Используя соотношения сторон, получим: $|AH - HB| = AC \cos(2x) - BC \cos x = AC$ (после подстановки и упрощения).
   Ответ: Разность отрезков равна стороне $AC$.
4. Задача 2. В равнобедренном треугольнике $ABC$ ($AB = BC$) на боковых сторонах взяты точки $M$ и $K$ так, что $BK = KM = AM = AC$. Найти $\angle ABC$.
   Решение:
   1. Пусть $AC = AM = BK = KM = x$. Тогда $AB = BC = 3x$.
   2. Треугольник $AMK$ равносторонний ($AM = KM = x$, $\angle A = 60^\circ$).
   3. Рассмотрим треугольник $ABC$: $\angle ABC = 180^\circ - 2\angle BAC = 180^\circ - 2 \cdot 60^\circ = 60^\circ$.
   Ответ: $\angle ABC = 60^\circ$.