8 800 707 6729
8 800 707 6729Telegram канал

Лицей «Вторая школа» из 7 в 8 класс 2020 год билет 11

Школа:
Сложность:
Дата экзамена: 2020
СкачатьПечать
youit.school ©

ЛИЦЕЙ ВТОРАЯ ШКОЛА


2020 год


Билет 11



Вопрос 27.



  • Определения: прямоугольник, ромб, квадрат
  • Свойство прямоугольника о диагоналях
  • Признак прямоугольника по диагоналям
  • Свойства диагоналей ромба
  • Признак ромба по диагоналям
  • Свойство ромба о перпендикулярных диагоналях
  • Признак ромба по перпендикулярным диагоналям


Вопрос 6.



  • Определения: биссектриса, медиана, высота, равнобедренный треугольник
  • Признак равнобедренности треугольника по равенству двух высот треугольника
  • Признаки равнобедренности треугольника по медиане, высоте, биссектрисе
  • (по парам: биссектриса и высота, биссектриса и медиана, высота и медиана)
  • (без использования суммы углов треугольника)


Задачи:



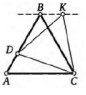
  1. Равнобедренные треугольники \(ABC\) и \(CDK\) расположены так, как показано на рисунке. Докажите, что прямая \(BK\) параллельна \(AC\).
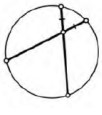
  2. Две хорды пересекаются так, что отмеченные на рисунке отрезки равны. Докажите, что сами хорды тоже равны.
Материалы школы Юайти
youit.school ©

Решения задач



  1. Вопрос 27:
    • Прямоугольник — параллелограмм с четырьмя прямыми углами. Свойство диагоналей: диагонали прямоугольника равны. Признак: если в параллелограмме диагонали равны, то это прямоугольник.
    • Ромб — параллелограмм с равными сторонами. Свойства диагоналей: диагонали ромба перпендикулярны и делят углы пополам. Признак ромба по диагоналям: если диагонали параллелограмма перпендикулярны, то это ромб.
    • Квадрат — прямоугольник и ромб одновременно: все стороны равны, все углы прямые, диагонали равны и перпендикулярны.


  2. Вопрос 6:
    • Биссектриса — луч, делящий угол пополам. Медиана — отрезок из вершины к середине противоположной стороны. Высота — перпендикуляр из вершины к противоположной стороне. Равнобедренный треугольник — треугольник с двумя равными сторонами.
    • Признаки равнобедренности:
      • Если медиана и высота совпадают, треугольник равнобедренный (доказывается через равенство треугольников $\triangle ABD$ и $\triangle CBD$ по катету и гипотенузе).
      • Если медиана и биссектриса совпадают, треугольник равнобедренный (доказывается через равенство углов при основании).
      • Если высота и биссектриса совпадают, треугольник равнобедренный (доказывается через равенство треугольников $\triangle ABH$ и $\triangle CBH$ по гипотенузе и острому углу).


  3. Задача 1:
    • Пусть $\triangle ABC$ равнобедренный с основанием $AC$, тогда $AB = BC$. $\triangle CDK$ равнобедренный с основанием $CK$, тогда $CD = DK$.
    • Углы при основании $\triangle ABC$: $\angle BAC = \angle BCA$. Аналогично, $\angle DCK = \angle DKC$.
    • Рассмотрим углы при точке $K$: $\angle BKC = \angle DKC = \angle DCK = \angle BCA$. Следовательно, $\angle BKC = \angle BAC$, что означает $BK \parallel AC$ (соответственные углы равны).
    Ответ: Прямые $BK$ и $AC$ параллельны.

  4. Задача 2:
    • Пусть хорды $AB$ и $CD$ пересекаются в точке $O$, причём $AO = OD$ и $CO = OB$ (по условию).
    • По теореме о пересекающихся хордах: $AO \cdot OB = CO \cdot OD$. Подставляя равенства отрезков: $AO^2 = CO^2$, откуда $AO = CO$.
    • Тогда длины хорд: $AB = AO + OB = CO + OD = CD$. Следовательно, $AB = CD$.
    Ответ: Хорды равны.
Материалы школы Юайти