Лицей «Вторая школа» из 7 в 8 класс 2020 год билет 10

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2020 год

Билет 10

Вопрос 14.

• Определения: ГМТ, прямоугольный треугольник, окружность, диаметр окружности
• Теорема о медиане, проведённой к гипотенузе
• Теорема о прямоугольном треугольнике с углом \(30^\circ\)
• Теорема о прямоугольном треугольнике с катетом, равным половине гипотенузы
• Теорема о медиане, проведённой к стороне треугольника (признак прямоугольности треугольника)
• Критерий прямоугольного треугольника (окружность)

Вопрос 28.

• Определения: средняя линия треугольника
• Теорема о средней линии треугольника
• Признак средней линии треугольника по средней стороне и параллельности
• Признак средней линии треугольника по параллельности и половине стороны
• Признак равнобедренности треугольника по равенству двух медиан треугольника

Задачи:

1. Противоположные стороны четырёхугольника попарно равны. Докажите, что его диагонали делятся точкой пересечения пополам, используя материал ранее: суммы углов треугольника.
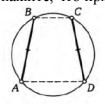
2. Хорды \(AB\) и \(CD\) окружности равны. Докажите, что прямые \(BC\) и \(AD\) параллельны.
   

Решения задач

1. Противоположные стороны четырёхугольника попарно равны. Докажите, что его диагонали делятся точкой пересечения пополам, используя материал ранее: суммы углов треугольника.
   Решение: Рассмотрим четырёхугольник ABCD, где AB = CD и BC = AD. Проведём диагонали AC и BD, пересекающиеся в точке O.
   Треугольники ABC и ADC равны по трём сторонам (AB = CD, BC = AD, AC — общая). Следовательно, ∠BAC = ∠DCA и ∠BCA = ∠DAC.
   Рассмотрим треугольники AOB и COD:
   • AB = CD (по условию)
   • ∠BAO = ∠DCO (из равенства треугольников ABC и ADC)
   • ∠ABO = ∠CDO (сумма углов треугольника: ∠ABO = 180° - ∠BAO - ∠AOB, аналогично для ∠CDO)
   Треугольники AOB и COD равны по стороне и двум прилежащим углам (ASA). Следовательно:
   AO = CO и BO = DO, что означает деление диагоналей точкой пересечения пополам.
   Ответ: Доказано.
   
   
2. Хорды \(AB\) и \(CD\) окружности равны. Докажите, что прямые \(BC\) и \(AD\) параллельны.
   Решение:
   • Равные хорды AB и CD стягивают равные дуги \(\smile AB = \smile CD\).
   • Вписанные углы, опирающиеся на эти дуги, равны: ∠BAD = ∠CDA (каждый равен половине дуги \(\smile BCD\) и \(\smile ABC\) соответственно).
   • Рассмотрим углы при секущей AD: ∠BAD = ∠CDA (доказано выше). Эти углы являются накрест лежащими при прямых BC и AD и секущей AD.
   По признаку параллельности прямых (равенство накрест лежащих углов) прямые BC и AD параллельны.
   Ответ: Доказано.