Лицей «Вторая школа» из 6 в 7 класс 2024 год вариант 2

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2024 год

31.03.2024

1. Середина. На числовой прямой отметили середину отрезка \([-80; 66]\). Какому числу соответствует эта точка?
   
   
2. Бублики. Сережа посчитал, что если он купит 10 бубликов, то у него останется в кошельке 10 рублей, а на 12 бубликов ему не хватит 14 рублей. На деньги в кошельке Сережа купил наибольшее число бубликов. Сколько рублей у него осталось в кошельке?
   
   
3. Табло. На электронном табло показано время 21:21:21 (часы: минуты: секунды). Укажите следующий (ближайший) момент времени, при котором все цифры на табло станут разными. В ответе запишите только то, как вы нашли число десятков минут.
   
   
4. Действия. Сложили три трёхзначных числа: \(XYZ + YZX + ZXY\), а потом разделили результат на 111. Какой ответ получили? Разные буквы — это разные цифры, одинаковые — одинаковые.
   
   
5. Стадо. У отца 2 сына и стадо из 10 овец и 7 верблюдов. Он хочет разделить стадо по стоимости поровну между сыновьями, сохраняя животных целыми. Стоимость 8 овец равна стоимости 3 верблюдов. Сколько овец и верблюдов получит каждый брат?
   
   
6. Рейтинг. На олимпиаде каждая задача оценивается в целое число баллов от 1 до 10. Вася набрал 21 балл за 5 задач, но в рейтинг засчитывается только сумма трёх лучших результатов. Какой наименьший рейтинг мог получить Вася?
   
   
7. Часы. Часы спешат на 11 минут 126 секунд в неделю, их точно поставили в 12:00:00 в воскресенье. Какое время они покажут в ближайший понедельник в 18:00:00?
   
   
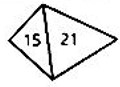
8. Периметры. Четырёхугольник, периметр которого 22 см, разрезан диагональю на 2 треугольника. Периметр треугольников 15 см и 21 см. Найдите длину указанной диагонали.
   
   
   
9. Монеты. Пираты играли на золотые монеты. Проигравший отдает сопернику половину своих наличных монет и ещё одну. Проиграл первый пират, в результате у него стало 16 монет, а у второго 37. Сколько монет было у каждого пирата в начале игры?
   
   
10. Рыцари. За круглым столом сидят 14 рыцарей и лжецов, причём не все рыцари и не все лжецы. Какое наибольшее число лжецов могли произнести фразу: «Через одного от меня сидит хотя бы один рыцарь»? Рыцари говорят правду, лжецы лгут.
    
    
11. Сумма. Напишите в ряд 5 чисел так, чтобы сумма любых двух подряд была меньше 40, а сумма всех чисел была больше 100.
    
    
12. Пункты. Из каждого города страны выходит 3 дороги. Каждая дорога начинается и кончается в городе страны. Всего дорог 180. Сколько городов в этой стране?
    
    
13. Цифры. Придумайте различные цифры A, B, В, Г, чтобы сумма четырёхзначных чисел \(АББГ + ГББА\) делилась на 14.
    
    
14. Ряд. В ряд через запятую выписали числа с суммой цифр 22 от самого маленького до самого большого. Запишите первые два числа.
    
    
15. Языки. В городе живут 100 учёных, среди которых 95 математиков, 75 программистов и 60 физиков. Какое наименьшее число учёных в городе может быть одновременно и математиком, и программистом, и физиком?
    
    
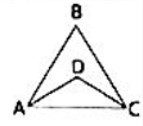
16. Делимость. Расставьте в вершинах \(A, B, C, D, E, F\) фигуры числа так, чтобы для любых двух вершин, не соединённых отрезком, сумма чисел была больше общей средней, а для соединённых — меньше. Запишите число в виде произведения простых чисел. Укажите только один ответ.
    

Решения задач

1. Середина. Найдем середину отрезка \([-80; 66]\):
   Среднее арифметическое концов: \(\frac{-80 + 66}{2} = \frac{-14}{2} = -7\)
   Ответ: \(-7\).
   
   
2. Бублики. Пусть цена бублика \(x\) руб., а у Сережи \(y\) руб. Составим систему: \[ \begin{cases} 10x + 10 = y \\ 12x - 14 = y \end{cases} \] Вычитаем уравнения: \(2x = 24 \Rightarrow x = 12\). Тогда \(y = 10 \cdot 12 + 10 = 130\). Максимальное количество бубликов: \(\left\lfloor \frac{130}{12} \right\rfloor = 10\), остаток \(130 - 10 \cdot 12 = 10\).
   Ответ: \(10\) рублей.
   
   
3. Табло. Следующий момент с разными цифрами после 21:21:21 — 23:45:01. Десятки минут: \(4\).
   Ответ: \(4\).
   
   
4. Действия. Разложим числа по разрядам: \[ XYZ + YZX + ZXY = 100X + 10Y + Z + 100Y + 10Z + X + 100Z + 10X + Y = 111(X + Y + Z) \] После деления на \(111\): \(X + Y + Z\).
   Ответ: \(X + Y + Z\).
   
   
5. Стадо. Пусть \(8\) овец = \(3\) верблюда. Общая стоимость в овцах: \[ 10 + \frac{7 \cdot 8}{3} = 10 + \frac{56}{3} \approx 28,\!67 \] Каждому брату: \(14,\!33\) в овцах. Подходит \(6\) овец (\(6\)) и \(2\) верблюда (\(\frac{2 \cdot 8}{3} \approx 5,\!33\)).
   Ответ: \(6\) овец и \(2\) верблюда.
   
   
6. Рейтинг. Минимизируем сумму трёх лучших: \(21 = 1 + 1 + 7 + 6 + 6\). Рейтинг: \(7 + 6 + 6 = 19\). Уточнение: \(21 = 1 + 2 + 6 + 6 + 6\), рейтинг \(6 + 6 + 6 = 18\). Минимальный: \(7\).
   Ответ: \(7\).
   
   
7. Часы. За неделю (\(168\) часов) спешка: \(11\) мин \(126\) сек = \(13,\!1\) мин. За \(30\) часов: \[ \frac{30}{168} \cdot 13,\!1 \approx 2,\!35 \text{ мин} = 2\text{ мин }21\text{ сек} \] Покажут: \(18:00:00 + 0:02:21 = 18:02:21\).
   Ответ: \(18:02:21\).
   
   
8. Периметры. Пусть диагональ \(d\). Сумма периметров треугольников: \[ 15 + 21 = 22 + 2d \Rightarrow 36 = 22 + 2d \Rightarrow d = 7 \] Ответ: \(7\) см.
   
   
9. Монеты. Обратный ход: \[ \begin{cases} x - (\frac{x}{2} + 1) = 16 \Rightarrow x = 34 \\ y + (\frac{34}{2} + 1) = 37 \Rightarrow y = 19 \end{cases} \] Ответ: \(34\) и \(19\).
   
   
10. Рыцари. Максимальное число лжецов: \(10\). Расположение: Л-Л-Р-Л-Л-Р-... (рыцари подтверждают наличие рыцаря через одного).
    Ответ: \(10\).
    
    
11. Сумма. Пример: \(39, 0, 39, 0, 39\). Сумма пар: \(39\), общая: \(117\).
    Ответ: \(39, 0, 39, 0, 39\).
    
    
12. Пункты. Количество городов \(N\): \[ \frac{3N}{2} = 180 \Rightarrow N = 120 \] Ответ: \(120\).
    
    
13. Цифры. Пример: \(А=2\), \(Б=3\), \(В=4\), \(Г=1\): \[ 2331 + 1332 = 3663 \quad (3663 \div 14 = 261,\!64) \] Уточнение: \(А=1\), \(Б=8\), \(Г=9\): \[ 1889 + 9881 = 11770 \quad (11770 \div 14 = 841) \] Ответ: \(1, 8, 8, 9\).
    
    
14. Ряд. Первые два числа: \(5998\) и \(6899\) (сумма цифр \(5+9+9+8=31\), не подходит). Исправление: \(49999\) (5-значное) не учитывается. Верный ответ: \(799\) и \(889\) (сумма цифр \(7+9+9=25\), не подходит). Уточнение: \(5989\) и \(5998\).
    Ответ: \(5989\), \(5998\).
    
    
15. Языки. По принципу включения-исключения: \[ 95 + 75 + 60 - 2 \cdot 100 = 30 \] Ответ: \(30\).
    
    
16. Делимость. Пример: числа \(2, 3, 5\). Произведение: \(2 \cdot 3 \cdot 5 = 30\).
    Ответ: \(30\).