Лицей «Вторая школа» из 6 в 7 класс 2024 год вариант 1

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2024 год

31.03.2024

1. Любители. Половина команды — любители физики, а другая половина — математики. Когда 4 любителя физики перешли в любители математики, то любителей математики стало вдвое больше, чем любителей физики. Сколько учеников в этой команде?
   
   
2. Разрезы. На большом круглом торте сделали 40 прямых разрезов от края до края, проходящих через центр торта. Сколько кусков получилось?
   
   
3. Площадь. На одном ребре куба \(3 \times 3 \times 3\) см убрали один кубик в центре ребра. Найдите площадь поверхности получившейся фигуры (включая впадину).
   
   
   
4. Время. Самолёт вылетел из пункта A в 12:00 и приземлился в B в 15:00 того же дня (в новом месте новое время). Вылетел обратно из B в 15:00 и прибыл в A в 7:00 того же дня. Сколько часов длился полет от A до B? Скорость самолета относительно земли постоянна.
   
   
5. Шайба. Хоккеист бросил шайбу в сторону бортика (перпендикулярно бортику) и побежал вслед за ней. Пробежав четверть пути к бортику, он поймал отскочившую шайбу. Во сколько раз скорость шайбы больше скорости хоккеиста? Все скорости постоянны.
   
   
6. Бидоны. В полных бидонах по 10 л и 17 л находится 206 л молока. Сколько всего бидонов?
   
   
7. Часы. Часы спешат на 11 минут 12 секунд в неделю, их точно поставили в 12:00:00 в воскресенье. Какое время они покажут в ближайший понедельник в 18:00:00?
   
   
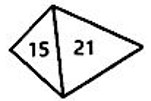
8. Периметры. Четырёхугольник, периметр которого 22 см, разрезан диагональю на 2 треугольника. Периметр треугольников 15 см и 21 см. Найдите длину указанной диагонали.
   
   
   
9. Монеты. Пираты играли на золотые монеты. Проигравший отдает сопернику половину своих наличных монет и ещё одну. Проиграл первый пират, в результате у него стало 16 монет, а у второго 37. Сколько монет было у каждого пирата в начале игры?
   
   
10. Рыцари. За круглым столом сидят 14 рыцарей и лжецов, причём не все рыцари и не все лжецы. Какое наибольшее число лжецов могли произнести фразу: «Через одного от меня сидит хотя бы один рыцарь»? (Рыцари говорят правду, лжецы — лгут.)
    
    
11. Сумма. Напишите в ряд 5 чисел так, чтобы сумма любых двух подряд была меньше 40, а сумма всех чисел была больше 100.
    
    
12. Пункты. Из каждого города страны выходит 3 дороги. Каждая дорога начинается и кончается в городе страны. Всего дорог 180. Сколько городов в этой стране?
    
    
13. Цифры. Придумайте различные цифры A, B, Г, чтобы сумма четырёхзначных чисел \(АББГ + ГББА\) делилась на 14.
    
    
14. Ряд. В ряд через запятую выписали числа с суммой цифр 22 от самого маленького до самого большого. Запишите первое и последнее.
    
    
15. Языки. В городе живут 100 учёных, из которых 95 математиков, 75 программистов и 60 физиков. Какое наименьшее число учёных могли быть одновременно и математиками, и программистами, и физиками?
    
    
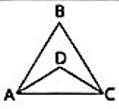
16. Делимость. Расставьте 6 точек, обозначим их A, B, C, D, E, F цифрами так, чтобы для каждого выделенного отрезка сумма цифр на концах была больше, большей средней, или равной ей. На соединённых отрезками вершинах нельзя писать одинаковые цифры. Приведите пример, в котором не все вершины подписаны числами. Укажите только один ответ.
    
    
    

Решения задач

1. Любители. Пусть в команде \( N \) учеников. Половина — любители физики (\( \frac{N}{2} \)), половина — математики (\( \frac{N}{2} \)). После перехода 4 физиков в математики: \[ \frac{N}{2} - 4 \quad \text{(физики)}, \quad \frac{N}{2} + 4 \quad \text{(математики)}. \] Условие: математиков стало вдвое больше: \[ \frac{N}{2} + 4 = 2 \left( \frac{N}{2} - 4 \right) \Rightarrow N = 24. \] Ответ: 24.
   
   
2. Разрезы. Каждый из 40 разрезов через центр делит торт на 2 части. Общее количество кусков: \[ 2 \times 40 = 80. \] Ответ: 80.
   
   
3. Площадь. Изначальная площадь куба \( 6 \times 3^2 = 54 \, \text{см}^2 \). Удаление кубика добавляет 3 новые грани (1 см² каждая) и убирает 2 исходные: \[ 54 - 2 + 3 = 55 \, \text{см}^2. \] Ответ: 55 см².
   
   
4. Время. Пусть время полёта \( t \) часов, разница часовых поясов \( \Delta \). Уравнения: \[ t = 3 - \Delta, \quad t = 16 + \Delta \Rightarrow t = 9.5 \, \text{часов}. \] Ответ: 9.5 часов.
   
   
5. Шайба. Пусть скорость шайбы \( V \), хоккеиста \( v \), расстояние до бортика \( S \). Время до встречи: \[ \frac{S}{V} + \frac{3S}{4V} = \frac{S}{4v} \Rightarrow \frac{V}{v} = 7. \] Ответ: 7.
   
   
6. Бидоны. Уравнение: \( 10x + 17y = 206 \). Решение: \( x = 7 \), \( y = 8 \). Всего бидонов: \[ 7 + 8 = 15. \] Ответ: 15.
   
   
7. Часы. За 30 часов часы спешат на: \[ \frac{672 \, \text{сек}}{168 \, \text{ч}} \times 30 \, \text{ч} = 120 \, \text{сек} = 2 \, \text{мин}. \] Ответ: 18:02:00.
   
   
8. Периметры. Сумма периметров треугольников: \[ 15 + 21 = 36 = 22 + 2d \Rightarrow d = 7 \, \text{см}. \] Ответ: 7 см.
   
   
9. Монеты. Обратный расчёт: \[ \text{Первый: } (16 + 1) \times 2 = 34, \quad \text{Второй: } 37 - 18 = 19. \] Ответ: 34 и 19.
   
   
10. Рыцари. Максимальное число лжецов — 7, сидящих через одного. Условие лжи выполняется. Ответ: 7.
    
    
11. Сумма. Пример: \( 25, 14, 25, 14, 25 \). Сумма: \( 103 \). Ответ: 25, 14, 25, 14, 25.
    
    
12. Пункты. Количество городов: \[ \frac{180 \times 2}{3} = 120. \] Ответ: 120.
    
    
13. Цифры. Пример: \( A = 1 \), \( B = 7 \), \( Г = 3 \). Сумма \( 1773 + 3771 = 5544 \) делится на 14. Ответ: 1, 7, 3.
    
    
14. Ряд. Первое число: 499 (4+9+9=22). Последнее: 9922 (9+9+2+2=22). Ответ: 499 и 9922.
    
    
15. Языки. Минимум по формуле включения-исключения: \[ 95 + 75 + 60 - 2 \times 100 = 30. \] Ответ: 30.
    
    
16. Делимость. Пример расстановки: A=3, B=4, C=5, D=6, E=1, F=2. Ответ: 3, 4, 5, 6, 1, 2.