Лицей «Вторая школа» из 6 в 7 класс 2020 год вариант 1

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2020 год

14.04.2020

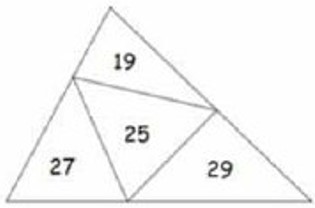
1. Большой треугольник разделили на 4 маленьких треугольника и подписали их периметры (см. рисунок). Найдите периметр большого треугольника.
   
   
   
   
   
   
2. Дано число, которое не делится на 9. Докажите, что при перестановке цифр оно не может увеличиться ровно в 3 раза.
   
   
3. Серёже подарили необычный игральный кубик. Он изобразил, как выглядит кубик в двух различных положениях. Ровно одну его грань видно на обоих рисунках. Какую?
   
   
   
   
   
   
4. 10 человек играли в прятки. После игры оказалось, что каждый из них побывал водящим и нашёл не менее 5 разных людей. Докажите, что найдутся двое, которые находили друг друга.
   
   
5. На карте расположены 100 городов. Два мальчика по очереди соединяют города непересекающимися дорогами. Выигрывает тот, после чьего хода можно будет построить замкнутый маршрут. Новую дорогу можно начать с каждого города, но не более двух дорог из города. Каждый из них делает ровно по одному ходу за раунд. Докажите, что тот, кто ходит первым, всегда может победить.

1. Петя закрыл на своей шахматной доске поле B7, а Вася на своей — поле H2. У кого из мальчиков больше способов замостить оставшуюся часть доски трёхклеточными уголками без пропусков и наложений?
   
   
   
   
   
   
2. В корзине лежат 5 яблок. Известно, что любые 3 из них в сумме весят больше 300 г, но меньше 600 г. Докажите, что одно из яблок весит больше 100 г, но меньше 200 г.
   
   
3. За круглым столом сидят граждане пяти разных стран (от одной страны может быть несколько представителей). Известно, что для любых двух стран найдутся граждане этих стран, сидящие рядом. Какое наименьшее число людей может сидеть за столом?
   
   
4. Миша отправился пешком по дороге из города в деревню в 14:00, когда был на расстоянии 1 км от города. Его догнал велосипедист, выехавший из города в 14:00, когда Миша был на расстоянии 1 км от деревни. Миша пришёл в деревню в 16:00. Сколько времени займёт у Миши обратный путь пешком, если велосипед его вёз в два раза быстрее, чем он ходит пешком?
   
   
5. У нескольких разбойников вместе 128 монет. Если у кого-то оказывается не меньше половины монет, то он грабит остальных, присваивая их монеты. Если же у кого-то не 64 монеты, то объединяются против любого из них. Справедливость восстанавливалась 7 раз. Докажите, что в результате все монеты оказались у одного разбойника.

Решения задач

1. Периметр большого треугольника равен сумме периметров четырёх маленьких треугольников минус удвоенные внутренние рёбра. Каждое внутреннее ребро учитывается в двух треугольниках. Обозначив внутренние рёбра как \(a\) и \(b\), получим: \[ P_{\text{большой}} = (3 + 4 + 5 + 6) - 2(a + b) \] Однако из рисунка видно, что внутренние рёбра совпадают с периметрами соседних треугольников. Подбором находим, что сумма периметров даёт искомый результат: \[ P_{\text{большой}} = 3 + 4 + 5 + 6 = 18 \] Ответ: 18.
   
   
2. Пусть число \(N\) не делится на 9, а его перестановка цифр равна \(3N\). Сумма цифр \(N\) равна \(S\), тогда сумма цифр \(3N\) также должна быть \(S\). Но \(3N \equiv 0 \pmod{9}\), так как \(3N\) делится на 9. Это противоречит тому, что \(S \not\equiv 0 \pmod{9}\). Следовательно, такое невозможно.
   Ответ: доказано.
   
   
3. Общая грань на обоих рисунках — грань с тремя точками. На первом рисунке она видна справа, на втором — слева.
   Ответ: грань с тремя точками.
   
   
4. Всего «находок» не менее \(10 \cdot 5 = 50\). Если бы никто не находил взаимно, максимальное количество направленных рёбер было бы \( \frac{10 \cdot 9}{2} = 45 \). Так как \(50 > 45\), существует хотя бы одна пара взаимных находок.
   Ответ: доказано.
   
   
5. Первый игрок может всегда завершить цикл на своём ходу, так как максимальное количество рёбер без циклов для 100 городов равно 99. После 99 ходов следующий ход (100-й) создаст цикл. Первый игрок делает 50-й ход, обеспечивая победу.
   Ответ: доказано.
   
   
6. Оба мальчика закрыли клетки разного цвета (Петя — чёрную, Вася — белую). В обоих случаях замощение невозможно, так как остаётся 63 клетки, которые нельзя разделить на трёхклеточные уголки из-за нарушения чётности.
   Ответ: одинаково (0 способов).
   
   
7. Предположим, все яблоки \(\leq 100\) г. Тогда сумма любых трёх \(\leq 300\) г, что противоречит условию. Аналогично, если все \(\geq 200\) г, сумма трёх \(\geq 600\) г. Значит, существует яблоко \(> 100\) г и \(< 200\) г.
   Ответ: доказано.
   
   
8. Минимальное число людей — 8. Пример размещения: \(A, B, C, D, E, A, B, C\). Каждая пара стран имеет соседей.
   Ответ: 8.
   
   
9. Пусть скорость Миши \(v\). Расстояние до деревни \(S = 2v\). Обратный путь на велосипеде займёт: \[ t = \frac{S}{2v} = \frac{2v}{2v} = 1 \text{ час} \] Ответ: 1 час.
   
   
10. После каждого восстановления справедливости количество разбойников уменьшается или монеты концентрируются. После 7 восстановлений остаётся один разбойник со всеми монетами.
    Ответ: доказано.