Лицей «Вторая школа» из 5 в 6 класс 2025 год вариант 1-1

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2025 год

1. Вычислить: $(0,4-0,044): 0,4$
2. ВРЕМЯ. Велосипедист проехал 100 м со скоростыо $20$ км/ч. Сколько секунд он ехал?
3. ЯЩИКИ. В двух ящиках $126$ кг песка. Если из первого пересыпать одну восьмую лежащего там песка во второй, то песка в ящиках станет поровну. Сколько кг песка было в первом ящике?
4. РОБОТЫ. $20$ роботов выполняют заказ за $14$ дней. Сколько роботов выполнят такой же заказ за $40$ дней?
5. ЦЕНЫ. У продавца было $7$ кг конфет «Зима» по $150$ руб./кг и $3$ кг конфет «Лето» по $170$ руб./кг. Он перемешал разнье конфеты. По какой цене за килограмм надо продавать смесь конфет, чтобы выручить те же деньги, если все конфеты будут проданы?
6. ЯБЛОКО. Царь наградил Емелю яблоком. В саду три сторожа, и каждый говорит Емеле: «При выходе из сада отдашь мне половину тех яблок, что будешь нести, да ещё одно». Сколько яблок должен взять Емеля, чтобы после расплаты со сторожами у него осталось одно яблоко?
7. ЗАМОК. В кодовом замке три окошка, в первом можно установить одну из 26 букв, во втором - одну их 10 цифр, а в третьем - одии из 5-и специальных символов. Сколько разных кодов можно набрать на этом замке?
8. ЗАГОТОВКИ. Из одной медной заготовки получается 6 деталей. Из обрезков от 6 заготовок делают еще одну заготовку. Сколько деталей можно получить из 36 заготовок, используя обрезки? (Если обрезков меньше, чем от 6 заготовок, то, заготовку и детали сделать нельзя).
9. КВАДРАТИКИ. Картонный квадрат со стороной 3 м разрезали на квадратики со стороной 5 см и положили их подряд в один ряд. Найдите дину полученного ряда в метрах.
10. СТРЕЛКИ. Какой угол образуют часовая и минутная стрелки в 1 час 20 минут? Ответ дайте в градусах. (Полная окружность 360 градусов. Стрелки часов движутся с постоянными скоростями.)
11. ПТИЦЫ. Когда голубь сидит на перилах, а воробей сидит на земле под голубем, то темечко голубя выше темечка воробья на 110 см. Когда воробей сидит на перилах, а голубь сидит на земле под воробьем, то темечко воробья выше темечка голуб́я на 90 см. На сколько сантиметров голубь выше воробья?
12. МЯЧ. Мяч стоит 5600 руб. Петя и Ваня договорились заплатить за него поровну, но у Пети было на руках только 2000 руб., поэтому Ваня внес 3600 руб. Ранее Петя давал Ване в долг 1000 руб. Скольо следует Ване отдать денег Пете, чтобы никто никому не был должен?
13. РЫЦАРИ. За круглым столом сидят 45 человек, рыцарей и лжецов, и не все они лжецы. Каждый произнес фразу: «Мои двое соседей (слева и сирава) разные - 1 рыцарь и 1 лжец». Сколько рыцарей за столом? Рыцари говорят правду, лжецы лгут.
14. РЯД, В ряд выписали числа с суммой цифр 20 от самого маленького до самого большого. Запишите первые два самых маленьких числа.
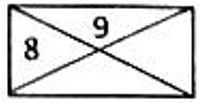
15. ПЕРИМЕТРЫ. Периметр прямоугольника 14 см, его разрезали по диагоналям на 4 треугольника, периметры двух соседних треугольников 8 см и 9 см. Найдите длину диагонали прямоугольника.
    
16. ПОХОД. В поход пошли 16 мальчишек. Каждый мальчишка, который надел сапоги, надел и кепку. Без сапог оказалось 10 мальчишек, а без кепки - двое. Сколько было тех, кто был в кепке, но без canor?

Решения задач

1. Вычислить: $(0,4-0,044): 0,4$
   Решение: $(0,4 - 0,044) : 0,4 = 0,356 : 0,4 = 0,89$
   Ответ: 0,89.
2. ВРЕМЯ. Велосипедист проехал 100 м со скоростью $20$ км/ч. Сколько секунд он ехал?
   Решение: Скорость 20 км/ч = $\frac{20 \cdot 1000}{3600} \approx 5,5556$ м/с. Время = $\frac{100}{5,5556} \approx 18$ секунд.
   Ответ: 18.
3. ЯЩИКИ. В двух ящиках $126$ кг песка. Если из первого пересыпать одну восьмую лежащего там песка во второй, то песка в ящиках станет поровну. Сколько кг песка было в первом ящике?
   Решение: Пусть в первом ящике $x$ кг. После пересыпания:
   $\frac{7x}{8} = 126 - x + \frac{x}{8} \Rightarrow 7x = 1008 - 8x + x \Rightarrow 14x = 1008 \Rightarrow x = 72$
   Ответ: 72 кг.
4. РОБОТЫ. $20$ роботов выполняют заказ за $14$ дней. Сколько роботов выполнят такой же заказ за $40$ дней?
   Решение: $20 \cdot 14 = x \cdot 40 \Rightarrow x = \frac{280}{40} = 7$
   Ответ: 7.
5. ЦЕНЫ. У продавца было $7$ кг конфет «Зима» по $150$ руб./кг и $3$ кг конфет «Лето» по $170$ руб./кг. Он перемешал разные конфеты. По какой цене за килограмм надо продавать смесь конфет, чтобы выручить те же деньги, если все конфеты будут проданы?
   Решение: Общая стоимость: $7 \cdot 150 + 3 \cdot 170 = 1560$ руб. Цена смеси: $\frac{1560}{10} = 156$ руб/кг.
   Ответ: 156 руб.
6. ЯБЛОКО. Царь наградил Емелю яблоком. В саду три сторожа, и каждый говорит Емеле: «При выходе из сада отдашь мне половину тех яблок, что будешь нести, да ещё одно». Сколько яблок должен взять Емеля, чтобы после расплаты со сторожами у него осталось одно яблоко?
   Решение: Пусть взял $x$ яблок. После трёх сторожей:
   $\frac{x}{8} - \frac{7}{4} = 1 \Rightarrow x = 22$
   Ответ: 22.
7. ЗАМОК. В кодовом замке три окошка, в первом можно установить одну из 26 букв, во втором — одну из 10 цифр, а в третьем — один из 5 специальных символов. Сколько разных кодов можно набрать на этом замке?
   Решение: $26 \cdot 10 \cdot 5 = 1300$
   Ответ: 1300.
8. ЗАГОТОВКИ. Из одной медной заготовки получается 6 деталей. Из обрезков от 6 заготовок делают еще одну заготовку. Сколько деталей можно получить из 36 заготовок, используя обрезки?
   Решение:
   $36 \rightarrow 216$ деталей + $6$ заготовок $\rightarrow 36$ деталей + $1$ заготовка $\rightarrow 6$ деталей. Итого: $216 + 36 + 6 = 258$
   Ответ: 258.
9. КВАДРАТИКИ. Картонный квадрат со стороной 3 м разрезали на квадратики со стороной 5 см и положили их подряд в один ряд. Найдите длину полученного ряда в метрах.
   Решение: Количество квадратиков: $\left(\frac{300}{5}\right)^2 = 3600$. Длина ряда: $3600 \cdot 5 = 18000$ см = 180 м.
   Ответ: 180 м.
10. СТРЕЛКИ. Какой угол образуют часовая и минутная стрелки в 1 час 20 минут?
    Решение: Часовая: $30 + \frac{20}{60} \cdot 30 = 40^\circ$. Минутная: $20 \cdot 6 = 120^\circ$. Разность: $120 - 40 = 80^\circ$.
    Ответ: $80^\circ$.
11. ПТИЦЫ. На сколько сантиметров голубь выше воробья?
    Решение: Пусть разница $h$ см. Система:
    $\begin{cases} h + \text{перила} = 110 \\ \text{перила} - h = 90 \end{cases} \Rightarrow h = 10$
    Ответ: 10 см.
12. МЯЧ. Мяч стоит 5600 руб. Сколько следует Ване отдать денег Пете, чтобы никто никому не был должен?
    Решение: Петя должен внести 2800 руб., но внес 2000. Ваня переплатил 800 руб. С учётом долга 1000: Ваня должен Пете 200 руб.
    Ответ: 200 руб.
13. РЫЦАРИ. Сколько рыцарей за столом? За круглым столом сидят \(45\) человек: рыцари и лжецы. Рыцари всегда говорят правду, а лжецы всегда врут.
    Каждый сказал: «Мои соседи — разные: один рыцарь, другой лжец.»
    
    Если это сказал рыцарь, то это правда, значит у него один сосед рыцарь, а другой лжец. Если это сказал лжец, то это ложь, значит у него оба соседа одинаковые.
    Попробуем начать с кусочка:
    Рыцарь, Рыцарь, Лжец
    Если продолжать по этому правилу, всё повторяется каждые три человека:
    (Р,\ Р,\ Л), (Р,\ Р,\ Л), (Р,\ Р,\ Л),...
    В каждом наборе из трёх человек два рыцаря и один лжец. Всего сидит \(45\) человек, а \(45\) делится на \(3\): \[ 45 \div 3 = 15 \] Значит таких троек \(15\), а рыцарей в каждой тройке \(2\): \[ 15 \times 2 = 30 \] Ответ: 30 рыцарей
14. РЯД. В ряд выписали числа с суммой цифр 20 от самого маленького до самого большого. Запишите первые два самых маленьких числа.
    Ответ: $299$, $389$.Если непонятно откуда берется ответ, ниже подробное решение
    Чтобы число было как можно меньше, левую цифру берём поменьше, а правые делаем побольше
    Из двух цифр сумма максимум $9+9=18$, значит нужно хотя бы три цифры
    Пробуем начинать с $1$: тогда оставшимся двум надо дать сумму $19$, но максимум $9+9=18$ — не хватает
    Значит первая цифра должна быть $2$, а оставшиеся две $9$ и $9$: получаем $299$ — это самое маленькое число
    Следующее число больше $299$ и с той же суммой
    С первой цифрой $2$ больше $299$ сделать нельзя: $29x$ при $x\le 9$ не превосходит $299$
    Берём первую цифру $3$, тогда две оставшиеся должны давать $17$
    Чтобы число было наименьшим, берём $8$ и $9$: получаем $389$
    Ответ: $299$ и $389$
    
15. ПЕРИМЕТРЫ. Найдите длину диагонали прямоугольника. Периметр прямоугольника 14 см, значит $2(a+b)=14$, откуда $a+b=7$
    Разрезали по двум диагоналям, каждый получившийся треугольник имеет одну сторону прямоугольника и две половинки диагоналей
    Значит периметр каждого такого треугольника равен «сторона + диагональ»
    Даны периметры двух соседних треугольников: $8$ и $9$, значит $a+d=8$ и $b+d=9$
    Вычтем: $(b+d)-(a+d)=9-8 \Rightarrow b-a=1$
    Теперь решим вместе с $a+b=7$: получаем $a=3$, $b=4$
    Из $a+d=8$ находим $d=8-3=5$
    Ответ: диагональ прямоугольника $5$ см
    
16. ПОХОД. Сколько было тех, кто был в кепке, но без сапог?
    Решение: В кепке 14 человек, из них 6 в сапогах. Значит, 14 - 6 = 8.
    Ответ: 8.