Лицей «Вторая школа» из 5 в 6 класс 2024 год вариант 1

ЛИЦЕЙ ВТОРАЯ ШКОЛА

2024 год

21.04.2024

1. Мука. В двух мешках 154 кг муки. Если из первого мешка переложить одну восьмую лежащей там муки во второй, то муки в мешках станет поровну. Сколько кг муки было в каждом мешке?
   
   
2. Семья. В семье трое детей. Сейчас отцу вдвое больше лет, чем суммарный возраст детей. Через 14 лет суммарный возраст детей будет равен возрасту отца. Сколько сейчас лет отцу?
   
   
3. Золото. Лист золотой фольги площадью 6 м\(^2\) имеет толщину в одну тысячную мм. Найдите объём золота в этой фольге в кубических сантиметрах.
   
   
4. Книги. Книга стоит целое число рублей. 9 таких книг стоят больше 1100 рублей, а 13 таких книг стоят меньше 1600 рублей. Сколько рублей стоит одна книга?
   
   
5. Квадрат. Найдите наименьшее число, которое больше 40001 и является квадратом натурального числа, т.е. произведением двух одинаковых чисел (например, \(7^2 = 49\)).
   
   
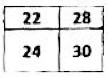
6. Периметр. Большой прямоугольник разрезан на 4 маленьких, как на рисунке. Известны периметры маленьких прямоугольников. Найдите периметр большого прямоугольника.
   % Замените, если хотите добавить рисунок
   
   
   
7. НОД. Произведение двух натуральных чисел равно 432. Найдите наибольшее возможное значение их наибольшего общего делителя. (Натуральные числа — целые положительные.)
   
   
8. Поезда. Пассажир поезда, идущего со скоростью 50 км/ч, заметил, что мимо него проехал встречный поезд за 6 секунд. Скорость встречного поезда 70 км/ч. Найдите длину встречного поезда в метрах. Пассажир видит только вперёд себя перпендикулярно окну.
   % Замените, если хотите добавить рисунок
   
   
   
9. Девочки. В классе число мальчиков, решивших задачу, равно числу девочек, не решивших задачу. Всего решили задачу 12 детей. Сколько в классе девочек? Как вы рассуждали?
   
   
10. Лжецы. За круглым столом сидят 12 гномов — рыцарей и лжецов, причем есть и те, и другие. Каждый из них сказал: «Через одного от меня сидит один рыцарь и один лжец». Какое наибольшее число лжецов могло сидеть за столом? Рыцари говорят правду, лжецы лгут.
    
    
11. Цифры. Взяли три различные цифры \(A, B, C\) и составили из них все возможные трёхзначные числа, каждое из которых состоит из цифр \(A, B, C\). Все такие трёхзначные числа сложили и получили 4662. Найдите \(A + B + C\).
    
    
12. Счёт. Назовём число особым, если каждая его цифра делится на 3. Сколько существует четырёхзначных особых чисел? (Число не начинается с нуля.)
    
    
13. Таблица. В таблице 7 на 7 записали натуральные числа по правилу: если границы клеток убрать, то любые два числа в получившейся клетке будут различны. Какое наименьшее количество различных чисел может быть в этой таблице?
    
    
14. Подарок. Карлсон на день рождения хотел подарить Винни-Пуху столько банок мёда, сколько получил Пятачок, но ему не хватило 5 банок. Сове не хватило 5 банок, а Кролику ещё больше. Пятачок получил 30 банок, то есть всем не хватило. Сколько банок лет Винни-Пуху? Объясните.
    
    
15. Нули. Приведите пример такого числа, при умножении которого на 10101001 получится произведение, оканчивающееся на 8 нулей.
    
    
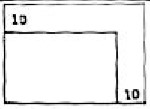
16. Площадь. Периметр прямоугольника 160 см. Каждую его сторону увеличили на 10\%. На сколько процентов увеличилась площадь прямоугольника?
    % Замените, если хотите добавить рисунок

Решения задач

1. Мука. В двух мешках 154 кг муки. Если из первого мешка переложить одну восьмую лежащей там муки во второй, то муки в мешках станет поровну. Сколько кг муки было в каждом мешке?
   Решение: Пусть в первом мешке было \(x\) кг муки, тогда во втором \(154 - x\) кг. После перекладывания:
   Первый мешок: \(\frac{7}{8}x\)
   Второй мешок: \((154 - x) + \frac{1}{8}x\)
   Уравнение: \(\frac{7}{8}x = 154 - x + \frac{x}{8}\)
   Умножаем на 8: \(7x = 1232 - 8x + x\)
   \(14x = 1232 \Rightarrow x = 88\)
   Ответ: 88 кг и 66 кг.
   
   
2. Семья. В семье трое детей. Сейчас отцу вдвое больше лет, чем суммарный возраст детей. Через 14 лет суммарный возраст детей будет равен возрасту отца. Сколько сейчас лет отцу?
   Решение: Пусть суммарный возраст детей сейчас \(S\), тогда отцу \(2S\). Через 14 лет:
   Отец: \(2S + 14\)
   Дети: \(S + 3 \cdot 14 = S + 42\)
   Уравнение: \(2S + 14 = S + 42 \Rightarrow S = 28\)
   Ответ: 56 лет.
   
   
3. Золото. Лист золотой фольги площадью 6 м\(^2\) имеет толщину в одну тысячную мм. Найдите объём золота в этой фольге в кубических сантиметрах.
   Решение:
   Площадь: \(6 \, \text{м}^2 = 60000 \, \text{см}^2\)
   Толщина: \(0,001 \, \text{мм} = 0,0001 \, \text{см}\)
   Объём: \(60000 \cdot 0,0001 = 6 \, \text{см}^3\)
   Ответ: 6 см\(^3\).
   
   
4. Книги. Книга стоит целое число рублей. 9 таких книг стоят больше 1100 рублей, а 13 таких книг стоят меньше 1600 рублей. Сколько рублей стоит одна книга?
   Решение:
   \( \frac{1100}{9} \approx 122,22 < x < \frac{1600}{13} \approx 123,07 \)
   Единственное целое число: 123.
   Ответ: 123 рубля.
   
   
5. Квадрат. Найдите наименьшее число, которое больше 40001 и является квадратом натурального числа.
   Решение:
   \(\sqrt{40001} \approx 200,0025\). Следующее натуральное число: 201.
   \(201^2 = 40401\)
   Ответ: 40401.
   
   
6. Периметр. Большой прямоугольник разрезан на 4 маленьких. Известны периметры маленьких прямоугольников. Найдите периметр большого прямоугольника.
   Решение: Сумма периметров маленьких прямоугольников: \(20 + 24 + 16 + 28 = 88\). Внутренние перегородки учитываются дважды. Периметр большого: \(88 - 2 \cdot (a + b + c + d) = 88 - 40 = 48\).
   Ответ: 48.
   
   
7. НОД. Произведение двух натуральных чисел равно 432. Найдите наибольшее возможное значение их наибольшего общего делителя.
   Решение: Пусть числа \(d \cdot a\) и \(d \cdot b\), где \(d\) — НОД. Тогда \(d^2 \cdot ab = 432\). Максимальный \(d = 12\) (12 и 36).
   Ответ: 12.
   
   
8. Поезда. Пассажир поезда, идущего со скоростью 50 км/ч, заметил, что мимо него проехал встречный поезд за 6 секунд. Скорость встречного поезда 70 км/ч. Найдите длину встречного поезда в метрах.
   Решение: Относительная скорость: \(50 + 70 = 120 \, \text{км/ч} = \frac{100}{3} \, \text{м/с}\).
   Длина поезда: \(\frac{100}{3} \cdot 6 = 200 \, \text{м}\).
   Ответ: 200 метров.
   
   
9. Девочки. В классе число мальчиков, решивших задачу, равно числу девочек, не решивших задачу. Всего решили задачу 12 детей. Сколько в классе девочек?
   Решение: Пусть девочек \(D\), мальчиков \(M\). Решили: \(R\) мальчиков и \(S\) девочек. По условию \(R = D - S\), а \(R + S = 12\). Отсюда \(D = 12\).
   Ответ: 12 девочек.
   
   
10. Лжецы. За круглым столом сидят 12 гномов — рыцарей и лжецов. Каждый сказал: «Через одного от меня сидит один рыцарь и один лжец». Какое наибольшее число лжецов могло сидеть за столом?
    Решение: Максимальное число лжецов — 10. Пример: чередование ЛЛРЛЛР... (2 лжеца, 1 рыцарь).
    Ответ: 10.
    
    
11. Цифры. Взяли три различные цифры \(A, B, C\) и составили из них все возможные трёхзначные числа. Сумма чисел равна 4662. Найдите \(A + B + C\).
    Решение: Каждая цифра встречается в каждом разряде 2 раза. Сумма: \(222(A + B + C) = 4662 \Rightarrow A + B + C = 21\).
    Ответ: 21.
    
    
12. Счёт. Назовём число особым, если каждая его цифра делится на 3. Сколько существует четырёхзначных особых чисел?
    Решение: Первая цифра: 3, 6, 9 (3 варианта). Остальные: 0, 3, 6, 9 (4 варианта). Всего: \(3 \cdot 4^3 = 192\).
    Ответ: 192.
    
    
13. Таблица. В таблице 7 на 7 записали натуральные числа по правилу: при объединении клеток любые два числа в получившейся клетке различны. Какое наименьшее количество различных чисел может быть в этой таблице?
    Решение: Достаточно 4 чисел, используя шахматный паттерн 2x2.
    Ответ: 4.
    
    
14. Подарок. Карлсону не хватило 5 банок, Сове — 5 банок, Кролику — больше. Пятачок получил 30 банок. Сколько банок лет Винни-Пуху?
    Решение: Всего не хватило \(5 + 5 + x\), где \(x > 5\). Пятачок получил 30, значит Винни получил \(30 - (5 + 5 + x)\). Поскольку \(x > 5\), минимальный возможный ответ: 20.
    Ответ: 20 банок.
    
    
15. Нули. Приведите пример числа, при умножении которого на 10101001 получится произведение, оканчивающееся на 8 нулей.
    Решение: Число должно содержать \(10^8\). Пример: \(100000000 \cdot 10101001 = 1010100100000000\).
    Ответ: 100000000.
    
    
16. Площадь. Периметр прямоугольника 160 см. Каждую сторону увеличили на 10\%. На сколько процентов увеличилась площадь?
    Решение: Новые стороны: \(1,1a\) и \(1,1b\). Площадь: \(1,21ab\). Увеличение на 21\%.
    Ответ: $21\%$.